Porovnání dvou závěsů
Úloha číslo: 370
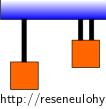
Na obrázku je na ocelovém lanku zavěšeno závaží. Totéž závaží je zavěšeno na dvou lankách poloviční délky. Porovnejte relativní a absolutní podélné prodloužení lanka.
Řešení úvahou
Předpokládejme, že působící síla nevytvoří v žádném lanku napětí větší, než je modul pružnosti oceli, a že se tedy bude jednat o pružnou deformaci, pro kterou platí Hookův zákon.
Relativní prodloužení lanka je přímo úměrné normálovému napětí, které je úměrné působící síle, protože lanka mají stejný obsah průřezu. V druhém případě, kdy těleso visí na dvou lankách, je působící síla poloviční než v prvním případě, proto i relativní prodloužení bude v druhém případě poloviční v porovnání s prvním případem.
Absolutní prodloužení je dáno součinem relativního prodloužení a původní délky lanka. Protože relativní prodloužení i původní délka jsou v druhém případě poloviční než v prvním, bude absolutní prodloužení v druhém případě čtyřikrát menší než v případě prvním.
Řešení výpočtem
Použijeme Hookův zákon:
\[\sigma = E \varepsilon,\]kde E je modul pružnosti oceli v tahu. Normálové napětí σ vyjádříme jako podíl velikosti působící síly F a obsahu průřezu lanka S:
\[\sigma = \frac{F}{S}.\]Relativní prodloužení ε je definováno jako podíl absolutního prodloužení Δl a původní délky lanka l:
\[\varepsilon = \frac{\Delta l}{l} \,.\]
Po dosazení těchto vztahů do Hookova zákona a můžeme vyjádřit vztah pro relativní prodloužení ε:
\[\frac{F}{S}= E \varepsilon\, \Rightarrow \, \varepsilon = \frac{F}{SE} \]a následně i pro absolutní prodloužení Δl:
Mezi délkami lanek v prvním a druhém případě platí vztah l1 = 2l2 a mezi velikostmi působících sil platí F1 = 2F2. Obsah průřezu S i modul pružnosti E je v obou případech stejný. Dosadíme tyto vztahy do výpočtu podílu prodloužení v obou případech.
\[\frac{\varepsilon _1}{\varepsilon _2}=\frac{\frac{F_1}{SE}}{\frac{F_2}{SE}} = \frac{F_1}{F_2}=\frac{2F_2}{F_2}=\frac{2}{1} ,\] \[\frac{\Delta l _1}{\Delta l_2}=\frac{\frac{F_1 l_1}{SE}}{\frac{F_2 l_2}{SE}} = \frac{F_1 l_1}{F_2 l_2}=\frac{2F_2 2l_2}{F_2 l_2}=\frac{4}{1}. \]Odpověď
Relativní prodloužení lanka je dvojnásobné a absolutní prodloužení čtyřnásobné v prvním případě než v případě druhém.




