Válcový vzorek polykrystalického materiálu
Úloha číslo: 2148
Válcový vzorek polykrystalického materiálu byl deformován jednoosým tahem. Počáteční délka vzorku byla 50 mm, průměr 6 mm. Deformační rychlost byla 3,3·10-4 s-1. Po 20 minutách deformování byla deformační síla 5,655 kN. Vypočítejte relativní a skutečnou deformaci a smluvní (tzv. inženýrské) a skutečné napětí po 20 minutách deformování vzorku. Poissonovo číslo uvažujte 0,5.
Zápis
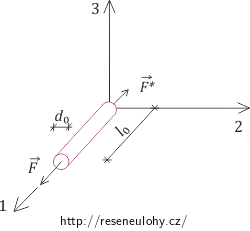
l0 = 50 mm počáteční délka vzorku d0 = 6 mm počáteční průměr vzorku \(\dot{\varepsilon}_0\) = 3,3·10-4 s−1 deformační rychlost F = 5,655 kN deformační síla po 20 minutách deformování μ = 0,5 Poissonovo číslo εr = ? relativní deformace po 20 minutách εT = ? skutečná deformace po 20 minutách σi = ? MPa smluvní napětí po 20 minutách σT = ? MPa skutečné napětí po 20 minutách Rozbor
Relativní deformaci po 20 minutách určíme ze známé rychlosti deformace a času. Relativní deformace uvažuje jen stav po 20 minutách, nikoliv děj, při kterém se délka postupně mění. Jestliže se tyč nějaké původní délky prodlouží o elementární délku (tzn. dost malou délku), pak při dalším prodloužení o elementární délku je třeba pro elementární relativní deformaci pro tuto část uvažovat už změněnou původní délku. Pro zohlednění tohoto děje se používá skutečná deformace. Tu můžeme získat jako součet všech elementárních relativních deformací při celkovém prodloužení. Smluvní napětí je napětí vztažené k původnímu průřezu vzorku. Pro skutečné napětí je třeba uvažovat průběh změny průměru průřezu vzorku analogicky jako průběh změny délky u skutečné deformace.
Nápověda
Stanovte při zadané deformační rychlosti relativní deformaci po 20 minutách. Relativní deformace zde znamená relativní prodloužení tyče, tak můžete určit i koncovou délku tyče po 20 minutách. Pro skutečnou deformaci uvažujte ve vztahu pro relativní deformaci prodloužení jen o elementární délku, to znamená hodně malou délku. Jinými slovy diferencujte vztah relativní deformace. Určitým integrálem od počáteční do koncové délky přes tento diferencovaný vztah již dostanete skutečnou deformaci. V integrálu uvažujte, že se délka postupně při zatěžování mění. Smluvní (inženýrské) napětí je jen klasický podíl síly a počátečního průřezu tyče. Pro skutečné napětí uvažujte deformaci průměru průřezu tyče podobně jako u skutečné deformace. Dále využijte Poissonovo číslo, které udává vztah mezi zúžením a prodloužením tyče. Nakonec dopočtěte průměr průřezu tyče po 20 minutách a skutečné napětí.
Řešení
Relativní deformaci můžeme přímo určit ze zadaných údajů o deformační rychlosti a době deformování, takže:
\[\varepsilon_\mathrm{r}\,=\,\dot{\varepsilon_0} t.\tag{1}\]Dosazením číselných hodnot do (1) dostáváme:
\[\varepsilon_\mathrm{r}\,=\,3{,}3{\cdot}10^{-4} \mathrm{s^{-1}}\cdot1200 \mathrm{s}\,=\,0{,}396.\]Jestliže známe relativní deformaci a počáteční délku, tak můžeme určit změnu délky vzorku. Pro relativní deformaci platí:
\[\varepsilon_\mathrm{r}\,=\,\frac{\Delta l}{l_0}.\]Odtud:
\[\Delta l\,=\,\varepsilon_\mathrm{r} l_0.\tag{2}\]Můžeme si také rovnou určit délku vzorku po 20 minutách deformování:
\[l^*\,=\,\Delta l+l_0\,=\,\varepsilon_\mathrm{r} l_0+l_0\,=\,l_0\left({\varepsilon_\mathrm{r}1}\right).\tag{3}\]Po číselném dosazení máme:
\[l^*\,=\,50{\cdot}10^{-3}\left({0{,}396+1}\right) \mathrm{m}\,=\,69{,}8{\cdot}10^{-3} \mathrm{m}.\]Ze vztahu (2) získáme pro prodloužení o elementární délku dl po diferencování:
\[\mathrm{d}\varepsilon_\mathrm{r}\,=\,\frac{\mathrm{d} l}{l_0}.\tag{4}\]Skutečnou deformaci získáme integrací (4) od počáteční do koncové délky vzorku. V integraci musíme ale ještě kvůli průběhu deformování odlišit původní délku ve vztahu (4) od délky l0 vzorku před zatěžováním. Takže:
\[\varepsilon_\mathrm{T}\,=\,\int_{l_0}^{l^*}\frac{\mathrm{d} l}{l}\,=\,\ln\left({\frac{l^*}{l_0}}\right).\tag{5}\]Číselně:
\[\varepsilon_\mathrm{T}\,=\,\ln\left({\frac{69{,}8{\cdot}10^{-3} \mathrm{m}}{50{\cdot}10^{-3} \mathrm{m}}}\right)\,=\,0{,}337.\]Smluvní napětí je síla vztažená na počáteční kolmý průřez vzorku:
\[\sigma_\mathrm{i}\,=\,\frac{F}{S_0}\,=\,\frac{4F}{\pi d_0^2}.\tag{6}\]Číselně:
\[\sigma_\mathrm{i}\,=\,\frac{4{\cdot} 5655}{\pi \cdot 36 {\cdot}10^{-6}} \mathrm{MPa}\,=\,200 \mathrm{MPa}.\]Zbývá už jen určit skutečné napětí. Pro zúžení vzorku zde budeme uvažovat analogický vztah jako u skutečné deformace při prodloužení. Využijeme Poissonovo číslo, které vyjadřuje vztah mezi zúžením a prodloužením.
\[\mu\,=\,\left|\frac{\varepsilon_\mathrm{zkrácení}}{\varepsilon_\mathrm{prodloužení}}\right|\]Jelikož Poissonovo číslo se udává kladné, musíme přidat záporné znaménko, protože se při prodloužení vzorek zúží, nikoliv rozšíří. Můžeme tedy psát:
\[\ln\left({\frac{d^*}{d_0}}\right)\,=\,-\mu\ln\left({\frac{l^*}{l_0}}\right).\tag{7}\]Pomocí pravidel při počítání s logaritmy můžeme ze (7) vyjádřit průměr průřezu po 20 minutách:
\[d^*\,=\,d_0\left({\frac{l_0}{l^*}}\right)^\mu.\tag{8}\]Po číselném dosazení do (8) je:
\[d^*\,=\,6{\cdot}10^{-3}\left({\frac{50}{69{,}8}}\right)^{0{,}5} \mathrm{m}\,=\,5{,}078{\cdot}10^{-3} \mathrm{m}.\]Už tedy můžeme vyjádřit skutečné napětí:
\[\sigma_\mathrm{T}\,=\,\frac{F}{S^*}\,=\,\frac{4F}{\pi {d^*}^2}.\tag{9}\]Stačí už jenom číselně vyjádřit skutečné napětí:
\[\sigma_\mathrm{T}\,=\,\frac{4{\cdot} 5655}{\pi \cdot 25{,}786 {\cdot}10^{-6}} \mathrm{MPa}\,=\,279 \mathrm{MPa}.\]Odpověď
Relativní deformace po 20 minutách je:
\[\varepsilon_\mathrm{r}\,=\,0{,}396.\]Skutečná deformace po 20 minutách je:
\[\varepsilon_\mathrm{s}\,=\,0{,}337.\]Dále jsme určili smluvní napětí:
\[\sigma_\mathrm{i}\,=\,200 \mathrm{MPa}.\]A ještě skutečné napětí je:
\[\sigma_\mathrm{s}\,=\,279 \mathrm{MPa}.\]

