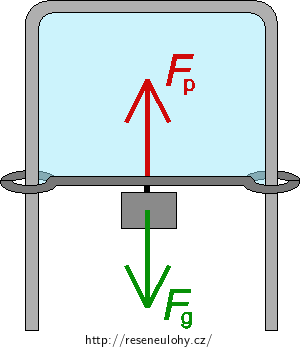
Mýdlová blána v rámu s pohyblivou příčkou
Úloha číslo: 2023
Na rámu s pohyblivou příčkou o délce 5 cm a hmotnosti 0,2 g je mýdlová blána, jejíž povrchové napětí je σ = 40 mN·m−1.
a) Jakým závažíčkem bychom udrželi pohyblivou příčku v rovnováze?
b) Jakou práci je třeba vykonat, abychom příčku posunuli o 1,5 cm?
Rozbor
Část a)
Vytvoříme-li v drátěném rámečku s pohyblivou příčkou mýdlovou blánu, bude se blána snažit zaujmout co nejmenší povrch. Blána bude na příčku působit povrchovou silou a posune ji tak, aby se povrch blány zmenšil. Chceme-li blánu udržet napjatou, musíme na pohyblivou příčku působit dostatečně velkou silou v opačném směru a zatížit ji například závažíčkem.
Část b)
Chceme-li posunout příčku, za kterou táhne napjatá blána, o určitou vzdálenost, musíme vykonat práci. Velikost této práce určíme jako součin konstantní síly, kterou na příčku budeme působit, a vzdálenosti, o kterou příčku posuneme.
Nápověda - Výpočet povrchové síly
Pro povrchovou sílu platí vztah
\[F_{\mathrm{p}} = σl,\]kde σ je povrchové napětí kapaliny a l je délka okraje povrchové blány, na který působí povrchová síla kolmo k povrchu kapaliny.
Mýdlová blána má dva povrchy, délku okraje této blány tedy musíme počítat dvakrát. Povrchovou sílu, kterou působí mýdlová blána na příčku, vypočítáme ze vztahu
\[F_{\mathrm{p}} = 2σl.\]Nápověda k části a)
Která další síla působí na příčku? Co musí platit pro výslednici sil působících na příčku, má-li být v rovnováze?
Nápověda k části b)
Jak velkou silou musíme na příčku působit, aby se posouvala rovnoměrným pohybem?
Řešení části a)
Velikost povrchové síly, kterou na příčku působí mýdlová blána, určíme ze vztahu
\[F_{\mathrm{p}} = 2σl.\]Na příčku dále působí tíhová síla daná její vlastní hmotností a hmotností závažíčka. Pro tíhovou sílu platí vztah
\[F_{\mathrm{g}} = mg.\]Má-li být pohyblivá příčka v rovnováze, musí být v rovnováze síly, které na příčku působí. Povrchová síla se musí rovnat tíhové síle:
\[F_{\mathrm{p}} = F_{\mathrm{g}},\]platí tedy
\[2σl = mg.\tag{1}\]Chceme znát hmotnost závažíčka, které příčku udrží v rovnováze. Ze vztahu (1) si vyjádříme hmotnost (jedná se ale o celkovou hmotnost závažíčka a příčky):
\[m = \frac{2σl}{g}.\tag{2}\]Dále do vztahu (2) dosadíme hodnoty známé ze zadání a vypočítáme celkovou hmotnost závažíčka a příčky
\[m \dot{=}\, \frac{2·40·10^{−3}·5·10^{−2}}{9{,}8} \mathrm{kg}\] \[m \dot{=}\, 4{,}1·10^{−4} \mathrm{kg}.\]Hmotnost závažíčka mz zjistíme snadno odečtením známé hmostnosti příčky mp od celkové hmotnosti m, kterou jsme právě vypočítali.
\[m_{\mathrm{z}} = m −m_{\mathrm{p}}\] \[m_{\mathrm{z}} = 4{,}1·10^{−4} kg − 2·10^{−4} kg\] \[m_{\mathrm{z}} = 2{,}1·10^{−4} kg.\]Řešení části b)
Působí-li konstantní síla velikosti F po dráze délky s, vykoná práci
\[W = F·s.\]V našem případě je síla F daná velikostí povrchové síly, kterou působí na příčku mýdlová blána.
Po dosazení dostaneme vztah
\[W = 2σl·s.\tag{3}\]Nyní do vztahu (3) dosadíme zadané hodnoty a vypočítáme, jak velkou práci vykonáme při posunutí příčky o 1,5 cm
\[W \dot{=}\, 2·40·10^{−3}·5·10^{−2}·1{,}5·10^{−2} \mathrm{J}\] \[W \dot{=}\, 6·10^{−5} \mathrm{J}.\]Odpověď
Pohyblivou příčku bychom udrželi v rovnováze závažíčkem o hmotnosti přibližně 0,2 g. Chceme-li příčku posunout o 1,5 cm, je potřeba vykonat práci 60 μJ.
Odkaz na experiment
Pokus k této úloze a k měření povrchového napětí mýdlové vody najdete zde: Mýdlová blána v rámu s pohyblivou příčkou.