Skleněné destičky ve vodě
Úloha číslo: 1865
Dvě svislé skleněné destičky částečně ponořené do vody spolu svírají velmi malý úhel ε. Udejte výšku h sloupce kapaliny jakožto funkci horizontální vzdálenosti x od hrany úhlu.
Nápověda
Klínovou vrstvu mezi skly si můžete představit vyplněnou svislými kapilárami. Vyjádřete, jak se mění průměr kapilár s rostoucí vzdáleností od hrany úhlu. Dále budete potřebovat znát vztah, který dává do souvislosti výšku, do níž vystoupí voda v kapiláře, s jejím průměrem.
Tabulkové hodnoty
Z tabulek:
ρ = 998,2 kg·m−3 hustota vody při 20 °C ρ0 = 1,2 kg·m−3 hustota vzduchu při 20 °C Rozbor
Zajímá nás, jaká bude výška sloupce vody mezi dvěma sklíčky, která se postupně rozevírají. Můžeme si představit, že prostor mezi sklíčky je vyplněn svisle postavenými kapilárami. S rostoucí vzdáleností od styčné hrany sklíček se zvětšuje i průměr kapilár. Postupně se tedy bude měnit i výška, do které vysoupí voda mezi sklíčky.
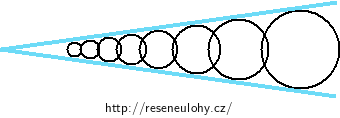
Abychom mohli odvodit závislost výšky vody na vzdálenosti od styčné hrany, potřebujeme jednak vědět, jak závisí výška, do které vystoupí voda, na průměru kapiláry. To zjistíme z rovnosti tlaků na zvolené stejné úrovni hladiny v nádobě a kapiláře.
Dále musíme zjistit, jak se mění průměr myšlených kapilár se vzdáleností od styčné hrany.
Teorie - Molekulární tlak
Molekuly v kapalině na sebe navzájem působí přitažlivými (kohezními) silami. Tyto síly působí pouze v malých vzdálenostech a s rostoucí vzdáleností od molekuly klesají. Kolem molekuly si můžeme představit kouli o takovém poloměru, že síly působící na molekulu mimo tuto kouli jsou zanedbatelné. Tento kulový prostor se nazývá sféra molekulárního působení.
Pokud je molekula i její sféra uvnitř kapaliny, pak je výslednice sil, kterými na sebe molekuly působí, rovna nule.
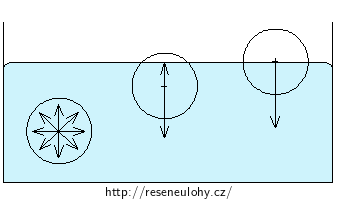
Molekuly, jejichž sféra molekulárního působení zasahuje nad hladinu vody, tvoří povrchovou vrstvu kapaliny. Na molekulu ležící v povrchové vrstvě kapaliny působí okolní molekuly kapaliny přitažlivými silami a výslednice těchto sil působí kolmo od povrchu kapaliny směrem dolů. Tato výsledná síla klesá se vzdáleností od hladiny kapaliny.
Na molekuly kapaliny v povrchové vrstvě působí ve svrchní části sféry molekuly plynů, které jsou nad hladinou. Výslednice těchto sil je také kolmá k povrchu, ale míří ven z kapaliny. S ohledem na to, že koncentrace molekul plynu je podstatně nižší než koncentrace molekul v kapalině, můžeme tuto sílu zpravidla zanedbat (v obrázku není zakreslena).
Povrch kapaliny se chová jako tenká pružná blána, díky tomu může jehla nebo lehká mince plovat na hladině.
Teorie - Kapilární jevy
Ke kapilárním jevům dochází v případě, kdy se kapalina stýká s vnitřní stěnou kapilár (úzkých trubic), které mají vnitřní průměr v řádu destin mm. Kapilární jevy se projevují zvýšením nebo snížením hladiny kapaliny v kapiláře oproti nádobě, do které je kapilára ponořena. U kapalin smáčejících stěny kapiláry dochází ke zvýšení hladiny, tomuto jevu říkáme kapilární elevace. U nesmáčejících kapalin hladina klesá, tento případ se nazývá kapilární deprese.
Ponoříme-li do nádoby s vodou několik skleněných kapilár o různých průměrech, zjistíme, že v kapiláře s menším průměrem vystoupá hladina výše, než v kapiláře s větším průměrem.
Změna výšky hladiny kapaliny, kterou pozorujeme v kapilárách, je důsledkem zakřivení povrchu kapaliny. Vlivem povrchového napětí vzniká v těchto případech přídavný kapilární tlak. Kapilární tlak je v každém místě kolmý k povrchu a přičítá se k molekulárnímu tlaku, což je tlak, který by působil na kapalinu s rovinným povrchem.
Povrch smáčivých kapalin je dutý (konvexní). Kapilární tlak míří ven z kapaliny a je záporný (odečítá se od molekulárního tlaku)
\[p = p_{m} − p_{k}.\]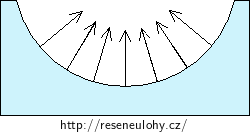
Nesmáčivé kapaliny mají vypuklý (konkávní) povrch, kapilární tlak zde směřuje do kapaliny a je kladný.
\[p = p_{m} + p_{k}.\]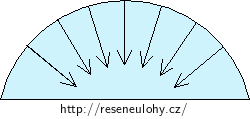
Řešení část 1 - Určení elevační výšky v kapiláře
Kapalina v nádobě i v kapiláře je v klidu. Tlaky na stejné úrovni vodorovné hladiny v nádobě i v kapiláře tedy musí být vyrovnané. Dále budeme porovnávat tlaky na úrovni volné hladiny kapaliny v nádobě.
Na povrchu kapaliny v nádobě je atmosférický tlak pa. Těsně pod povrchem se k atmosférickému tlaku přičítá molekulární tlak pm.
Na stejné úrovni hladiny je v kapiláře atmosférický tlak pa zmenšený o tlak sloupce plynu takové výšky h, jakou má sloupec kapaliny v kapiláře. Pro tlak plynu o hustotě ρ0 platí
\[p = hρ_{0}g.\]Dále se zde uplatňuje molekulární tlak pm. Je-li kapalina smáčivá, má konvexně zakřivený povrch a molekulární tlak je zmenšen o kapilární tlak
\[p_k = \frac{2σ}{R},\]kde R je vnitřní poloměr kapiláry.
Poznámka: Odvození vztahu pro kapilární tlak lze najít v úloze Skleněná trubička a mýdlové bubliny.
Musíme ještě přičíst hydrostatický tlak sloupce kapaliny o výšce h, jejíž hustota je ρ.
Pro rovnovážný stav kapaliny v kapiláře a v nádobě platí vztah
\[p_a + p_{m} = p_a - hρ_{0}g + p_{m} - \frac{2σ}{R} + hρg.\]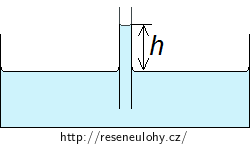
Z tohoto vztahu můžeme vyjádřit elevační výšku h
\[h = \frac{2σ}{R(ρ - ρ_{0})g}.\tag{1}\]Porovnáme-li hustotu vody s hustotou vzduchu, zjistíme, že hustota vody je přibližně 800x větší, než hustota vzduchu. Hustotu vzduchu tedy můžeme zanedbat a dostaneme tak jednodušší vztah pro elevační výšku
\[h = \frac{2σ}{Rρg}.\tag{2}\]Ze vztahu (2) je vidět, že s rostoucím průměrem kapiláry klesá výška, do které kapalina vystoupí.
Poznámka: Elevační výška nesmáčivých kapalin
Sloupec nesmáčející kapaliny je v kapiláře snížen o výšku h.
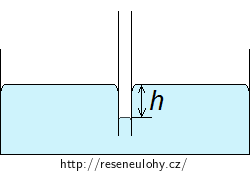
Na povrchu kapaliny v nádobě je stejně jako u smáčivé kapaliny atmosférický tlak pa, ke kterému se těsně pod povrchem přičítá molekulární tlak pm.
Na povrchu kapaliny v kapiláře je také atmosférický tlak pa, ten je ale zvětšen o tlak sloupce plynu hustoty ρ0 o výšce h . Dále se uplatňuje molekulární tlak pm, ke kterému se vlivem konkávně zakřiveného povrchu kapaliny přičítá kapilární tlak. Poté ještě musíme odečíst tlak sloupce kapaliny o výšce h. Pokud jsou všechny tlaky v rovnováze, pak platí
\[p_a + p_{m} = p_a + hρ_{0}g + p_{m} + \frac{2σ}{R} - hρg.\]Po úpravě tohoto vztahu dostaneme
\[h = \frac{2σ}{R(ρ − ρ_0)g}.\]Při zanedbání hustoty vzduchu ρ0 oproti hustotě kapaliny ρ dostaneme vztah
\[h = \frac{2σ}{Rρg}.\]Pro snížení hladiny nesmáčivé kapaliny tedy platí stejný vztah, jako pro zvýšení hladiny smáčivé kapaliny.
Řešení část 2 - Závislost poloměru kapiláry na vzdálenosti od hrany úhlu
Ponoříme-li do kapaliny dvě sklíčka, která budou svírat malý úhel ε, vystoupá hladina v místě dotyku sklíček nejvýše, protože myšlená kapilára tam má nejmenší průměr. Se vzdáleností od místa dotyku dvou sklíček bude výška hladiny klesat. Dále se budeme snažit zjistit, jak závisí průměr kapiláry R na vzdálenosti x od hrany úhlu.
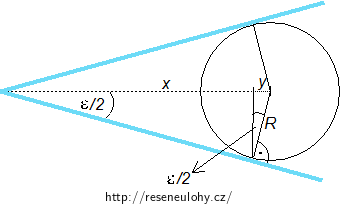
Z velkého trojúhelníku vyjádříme sin ε/2
\[sin \frac{ε}{2} =\frac{R}{x+y}\]a upravíme tak, abychom měli x+y na levé straně
\[x+y = \frac{R}{sin\frac{ε}{2}}.\tag{3}\]Dále z malého trojúhelníku také vyjádříme sin ε/2
\[sin \frac{ε}{2} =\frac{y}{R}\]a osamostatníme y
\[y = R·sin \frac{ε}{2}.\tag{4}\]Nyní můžeme y ze vztahu (4) dosadit do vztahu (3) a dostaneme
\[x+R·sin \frac{ε}{2} = \frac{R}{sin\frac{ε}{2}}\]rovnici upravíme, abychom osamostatnili R
\[x = R\left(\frac{1}{sin \frac{ε}{2}} −sin \frac{ε}{2}\right)\] \[R = x\left(\frac{sin \frac{ε}{2}}{1 −sin^{2} \frac{ε}{2}}\right)\]úhel ε/2 je ale velmi malý, sinus tohoto úhlu bude tedy také malý a blízký 0. Po umocnění sinu na druhou dostaneme ještě menší číslo, které už se přibližně bude rovnat 0. Po zanedbání členu sin2 ε/2 nám ve jmenovateli zlomku zůstane jen číslo 1. Pro R, které hledáme, tedy bude platit
\[R = x·sin \frac{ε}{2}.\tag{5}\]Jiné vyjádření závislosti poloměru kapiláry R na vzdálenosti od hrany úhlu
Jelikož úhel ε/2 je velmi malý a pro malé úhly platí sin α = tg α, tedy
\[sin \frac{ε}{2} =tg \frac{ε}{2} = \frac{R}{x+y}\]Dvě sklíčka jsou blízko u sebe, úhel ε/2 je tedy velmi malý a proto je strana y, která leží v malém trojúhelníčku proti úhlu ε/2, velmi krátká. Vzdálenost y tedy můžeme zanedbat. Dostáváme vztah
\[sin \frac{ε}{2} = \frac{R}{x} \]a z tohoto vztahu už jen vyjádříme poloměr kapiláry R
\[R = x·sin\frac{ε}{2}.\]Vyjádření výšky hladiny
Odpověď
Vypočítali jsme, že výška hladiny kapaliny závisí na vzdálenosti x od hrany úhlu vztahem
\[h = \frac{1}{x}·\frac{2σ}{ρgsin\frac{ε}{2}}.\]Podle tohoto vztahu se bude výška hladiny měnit pouze v závislosti na 1/x, všechny ostatní veličiny jsou konstantní. Hladina kapaliny mezi sklíčky tedy bude mít tvar hyperboly.
Odkaz na experiment
Pokus k této úloze si můžete prohlédnout zde: Skleněné destičky ponořené ve vodě, aneb kapilární vzlínavost na klínu.




