Sbírka řešených úloh

Zahřátí ocelové tyče

Úloha číslo: 2094

Ocelová tyč je pevně upnutá na obou koncích a při teplotě 10 °C je v nenapjatém stavu. Jaké je v tyči napětí, stoupne-li její teplota na 100 °C?

 

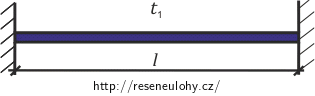
• Zápis

  t1 = 10 °C	původní teplota v nenapjatém stavu
  t2 = 100 °C	teplota po změně

  Z tabulek:

  E = 210·103 MPa	Youngův modul pružnosti oceli v tahu
  α = 1,2·10-5 K−1	koeficient teplotní délkové roztažnosti oceli
  σ = ? Pa	napětí v tyči po změně teploty

• Rozbor

  Při změně teploty dochází ke změně délky tyče. Tyč je ale pevně upnutá a nemůže se prodloužit. V tyči bude proto vznikat napětí. Když budeme znát závislost změny délky tyče na změně teploty, tak si můžeme vyjádřit její relativní prodloužení. Pak již stačí napsat vztah mezi napětím a relativním prodloužením tyče.

• Nápověda

  Připomeňte si, jak závisí prodloužení tyče na změně teploty, a vyjádřete si relativní prodloužení tyče při dané změně teploty. Dále využijte vztah vyjadřující závislost napětí na relativním prodloužení tyče.

• Řešení

  Prodloužení tyče závisí na změně teploty následujícím vztahem:

  \[\Delta l\,=\, l_1 \alpha \left({t_2-t_1}\right),\]

  kde l₁ je počáteční délka tyče při teplotě t₁.

  Relativní prodloužení tyče je pak rovno:

  \[\varepsilon\,=\,\frac{\Delta l}{l_1}\,=\,\alpha \left({t_2-t_1}\right).\tag{1}\]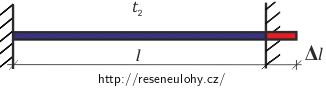

   

  

  Tyč je pevně upnutá, musí si tedy uchovat svoji délku. K tomu je zapotřebí tlakového napětí:

  \[\sigma\,=\,E\varepsilon.\tag{2}\]

  Stačí už jenom dosadit (1) do (2):

  \[\sigma\,=\,E\alpha \left({t_2-t_1}\right).\tag{3}\]

  Po číselném dosazení do (3) máme:

  \[\sigma\,=\,210{\cdot}10^{9}\cdot1{,}2{\cdot}10^{-5}\cdot\left({100-10}\right)\mathrm{Pa}\,=\,22{,}68{\cdot}10^{7} \mathrm{Pa}.\]

• Odpoveď

  Po změně teploty je v tyči napětí:

  \[\sigma\,=\,22{,}68{\cdot}10^{7} \mathrm{Pa}.\]