Sbírka řešených úloh

Účinnost Ottova cyklu

Úloha číslo: 412

• Nápověda

  a) Rozmyslete si, zda není možné spočítat práci plynu, kterou plyn vykoná během jednoho cyklu cyklického děje, bez použití vzorců pro práci.

  b) Zkuste upravit Poissonův zákon tak, aby v něm vystupovala termodynamická teplota.

• Řešení nápovědy b)

  Poissonův zákon má tvar pV^κ = C = konst., kde jsme konstantu označili C. Nyní si ze stavové rovnice pro ideální plyn vyjádříme tlak

  $$\frac{pV}{T} = K \quad\Rightarrow\quad p = \frac{T}{V} K,$$

  kde K je opět konstanta.

  Vyjádřený tlak dosadíme do Poissonova zákona, rovnici upravíme a konstanty (C a K) dáme na jednu stranu:

  $$pV^{\kappa} = C \quad\Rightarrow\quad\frac{T}{V}V^{\kappa} K = C \quad\Rightarrow \quad TV^{\kappa - 1} = \frac{C}{K} = \mathrm{konst.}$$

• Rozbor

  Abychom mohli vyjádřit účinnost Ottova cyklu, musíme znát práci vykonanou plynem během jednoho oběhu a teplo, které plyn během jednoho cyklu přijal. Účinnost je pak podíl práce a dodaného tepla.

  Pro kruhové děje platí, že změna celkové vnitřní energie plynu během jednoho oběhu je nulová. To nastává díky tomu, že plyn má na začátku i na konci každého cyklu stejný stav a že vnitřní energie je stavová veličina (její změna závisí pouze na počátečním a koncovém stavu, nikoli na průběhu děje). Podle prvního termodynamického zákona tedy platí, že práci plynu lze vyjádřit jako rozdíl tepla dodaného a odevzdaného.

  Protože při adiabatických dějích se teplo nepředává, tak plyn přijme teplo pouze při izochorickém zahřátí a odevzdá teplo při izochorickém ochlazení.

  Dodané a odevzdané teplo spočítáme pomocí molární tepelné kapacity při konstantním objemu. Po určení těchto tepel již můžeme vyjádřit účinnost Ottova cyklu. Pro vyjádření účinnosti pomocí kompresního poměru a Poissonovy konstanty využijeme Poissonův zákon upravený pomocí stavové rovnice pro ideální plyn tak, že se v něm vyskytuje termodynamická teplota místo tlaku.

• Řešení

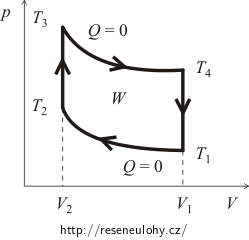
  Na počátku je jako obvykle třeba získat představu o tom, jak uvedený cyklus vypadá v p–V diagramu. K tomu nám poslouží znalosti o průběhu izochor a adiabat. Přibližný nákres Ottova cyklu je patrný z následujícího obrázku.

  

  Účinnost η cyklu je definována jako

  $$\eta = \frac{W}{Q_{dod}},$$

  kde W je práce vykonaná během jednoho cyklu plynem zmenšená o práci vykonanou vnějšími silami (v diagramu je znázorněna jako obsah plochy ohraničené cyklem!) a Q_dod teplo dodané během oběhu do systému.

  Práci W bychom mohli spočítat díky znalosti vztahů mezi tlakem a objemem během adiabatické expanze a komprese (při izochorických dějích je práce samozřejmě nulová). V této úloze však bude výhodnější vyjít z toho, že celková změna vnitřní energie za celý cyklus musí být rovna nule (dostáváme se zase do stejného stavu jako na začátku, tudíž je stejná teplota, a tedy i vnitřní energie!). Z 1. termodynamického zákona pak vyplývá, že práci plynu lze vyjádřit jako rozdíl dodaného tepla Q_dod a odevzdaného tepla Q_od. Vzorec pro účinnost cyklu tak můžeme přepsat do tvaru:

  $$\eta = \frac{W}{Q_{dod}} = \frac{Q_{dod}-Q_{od}}{Q_{dod}}.$$

  Nejprve spočteme dodané teplo Q_dod. Je jasné, že při adiabatických dějích tepelná výměna vůbec neprobíhá, a při izochorickém ochlazení je teplo ze systému naopak odebíráno. Díky tomu bude teplo dodáváno pouze během izochorického zahřátí z teploty T₂ na T₃. Velikost tohoto tepla lze pomocí látkového množství plynu n a jeho molární tepelné kapacity C_V vyjádřit následovně:

  $$Q_{dod} = nC_{V}\left( T_{3}-T_{2} \right)$$

  Velmi podobným způsobem vyjádříme i velikost odevzdaného tepla Q_od. Již víme, že k odevzdávání dochází pouze při izochorickém ochlazení z teploty T₄ zpět na počáteční teplotu T₁. Díky tomu bude platit:

  $$Q_{od} = nC_{V}\left( T_{4}-T_{1} \right)$$

  Dosazením do vzorce pro účinnost cyklu pak okamžitě dostáváme:

  $$\eta = \frac{Q_{dod}-Q_{od}}{Q_{dod}} = \frac{nC_{V}\left( T_{3}-T_{2} \right) - nC_{V}\left( T_{4}-T_{1} \right)}{nC_{V}\left( T_{3}-T_{2} \right)} =$$ $$=1 - \frac{T_{4} - T_{1}}{T_{3} - T_{2}}$$

  Nyní bude potřeba nějakým způsobem vyjádřit rozdíly teplot pomocí zadaného kompresního poměru

  $$r=\frac{V_{1}}{V_{2}}$$

  a Poissonovy konstanty κ.

  K tomu se nám bude hodit Poissonův zákon pV^κ = C = konst., kde jsme konstantu označili C a který upravíme pomocí stavové rovnice pro ideální plyn

  $$\frac{pV}{T} = K \quad\Rightarrow\quad p = \frac{T}{V} K$$

  Vyjádřený tlak dosadíme do Poissonova zákona, rovnici upravíme a konstanty (C a K) dáme na jednu stranu:

  $$pV^{\kappa} = C \quad\Rightarrow\quad\frac{T}{V}V^{\kappa} K = C \quad\Rightarrow \quad TV^{\kappa - 1} = \frac{C}{K} = \mathrm{konst.}$$

  Takto upravený Poissonův zákon postupně uplatníme pro oba adiabatické procesy. Pro adiabatickou expanzi dostáváme vztah

  $$T_{4}V_{1}^{\kappa - 1} = T_{3}V_{2}^{\kappa - 1},$$

  pro adiabatickou kompresi poté

  $$T_{1}V_{1}^{\kappa - 1} = T_{2}V_{2}^{\kappa - 1}.$$

  Nyní odečteme druhou rovnici od první a vytkneme V₁^{κ − 1} na straně jedné a V₂^κ − 1 na straně druhé a získáme:

  $$\left( T_{4}-T_{1}\right) V_{1}^{\kappa -1} = \left( T_{3}-T_{2}\right) V_{2}^{\kappa -1} \Rightarrow \frac{T_{4}-T_{1}}{T_{3}-T_{2}} = \left( \frac{V_{2}}{V_{1}}\right) ^{\kappa - 1} \Rightarrow$$ $$\Rightarrow \frac{T_{4}-T_{1}}{T_{3}-T_{2}} = \left( \frac{1}{r}\right) ^{\kappa - 1}$$

  Vidíme, že se nám rozdíly teplot skutečně podařilo vyjádřit pomocí zadaných veličin. Dosazením do vzorce pro účinnost pak dostáváme konečný vzorec:

  $$\eta = 1-\frac{T_{4}-T_{1}}{T_{3}-T_{2}} = 1-\left( \frac{1}{r}\right) ^{\kappa - 1}$$ $$\eta = 1-r^{1-\kappa}$$

• Odpověď

  Účinnost Ottova cyklu je tedy dána vztahem

  $$\eta = 1-r^{1-\kappa}.$$