Bimetal
Úloha číslo: 366
Měděný a zinkový pásek mají při teplotě 20 °C stejnou délku 20 cm.
a) O kolik se bude lišit jejich délka při teplotě 100 °C?
b) Pásky byly při teplotě 20 °C snýtovány a vytvořily tzv. bimetal. Předpokládejme, že se při zahřívání ohýbá do oblouku. Určete, který kov bude na vnější straně oblouku a jaký bude poloměr tohoto oblouku při teplotě 100 °C, jestliže jsou 1 mm silné.

Zápis
t0 = 20 °C teplota, při které jsou oba pásky stejně dlouhé l0 = 20 cm = 0,20 m délka obou pásků při teplotě t0 t = 100 °C teplota, na kterou pásky ohřejeme Δl = ? rozdíl délek obou pásků při teplotě t d = 1 mm = 1·10−3 m tloušťka obou pásků r = ? poloměr ohnutého bimetalu Z tabulek αZn = 30·10−6K−1 teplotní součinitel délkové roztažnosti zinku αCu = 17·10−6K−1 teplotní součinitel délkové roztažnosti mědi Rozbor
Látky se při zvyšování teploty roztahují. Různé látky se roztahují různě, proto vznikne délkový rozdíl mezi oběma pásky. Jestliže jsou oba pásky pevně snýtovány tak, že se po sobě nemohou posouvat, dojde k jejich ohnutí. Pásek, který se roztahuje méně, bude na vnitřní straně. V našem případě se jedná o měď. Díky tloušťce pásků se oba oblouky liší svoji délkou. Rozdíl délek obou oblouků musí odpovídat rozdílu délek, který způsobila odlišná teplotní roztažnost obou kovů.
Řešení a)
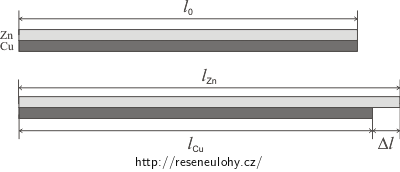
Nejprve vyjádřeme délky obou pásků při teplotě t.
\[l_{Cu}=l_0\,(1+\alpha_{Cu}\Delta t)\] \[l_{Zn}=l_0\,(1+\alpha_{Zn}\Delta t)\]Obě délky odečteme:
\[\Delta l=l_{Zn}-l_{Cu}\] \[\Delta l=l_0\,(1+\alpha_{Zn}\Delta t)-l_0\,(1+\alpha_{Cu}\Delta t)\] \[\Delta l=l_0\,(\alpha_{Zn}-\alpha_{Cu})\Delta t\] \[\Delta l=l_0\,(\alpha_{Zn}-\alpha_{Cu})\,\left(t-t_0\right)\]A dosadíme číselné hodnoty:
\[\Delta l=l_0\,(\alpha_{Zn}-\alpha_{Cu})\,\left(t-t_0\right)\] \[\Delta l=0{,}2\cdot\,(30\cdot{10^{-6}}-17\cdot{10^{-6}})\cdot\,\left(100-20\right)\,\mathrm{m}\] \[\Delta l=2{,}08\cdot{10^{-4}}\,\mathrm{m}=0{,}208\,\mathrm{mm}\]Nápověda b) Jak určit poloměr bimetalu?
Protože jsou pásky pevně snýtovány k sobě, dojde při ohřátí k jejich deformaci. Uvažujme, že délku, která odpovídá zvýšené teplotě, má daný pásek uprostřed.
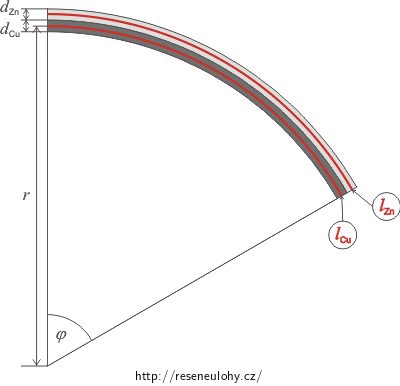
Délku obou pásků jsme jednak vyjádřil v části a), jednak ji můžeme vyjádřit pomocí úhlu φ a poloměru hledaného r. A odtud se nám již podaří určit poloměr r.
Pozn.: Při zvýšení teploty dojde i k zvýšení tloušťky obou pásků. Tento efekt má ale na výsledný velmi malý vliv, proto ho můžete případně zanedbat.
Řešení b)
Při výpočtu poloměru vzniklého oblouku budeme vycházet z obrázku. Protože jsou pásky pevně snýtovány k sobě, dojde k jejich deformaci. Budeme uvažovat, že délku, která odpovídá zvýšené teplotě, má pásek uprostřed.

Poloměr menšího oblouku si označíme r. Větší oblouk má poloměr R
\[R=r+\frac{d_1+d_2}{2}\]kde d1 a d2 jsou „zvětšené“ tloušťky obou pásků. Délka kruhového oblouku je dána součinem poloměru a úhlu φ (vyjádřeného v obloukové míře, tj. v radiánech).
\[l_{Cu}=r\varphi\] \[l_{Zn}=(r+\frac{d_{Zn}}{2}+\frac{d_{Cu}}{2})\varphi\]Obě délky odečteme a uvědomíme si, že jejich rozdíl se musí rovnat rozdílu v délkách obou pásků, který jsme vyjádřili v části a) této úlohy.
\[\Delta l=l_{Zn}-l_{Cu}=(r+\frac{d_{Zn}}{2}+\frac{d_{Cu}}{2})\varphi-r\varphi=\frac{1}{2}(d_{Zn}+d_{Cu})\varphi\]Dosadíme za rozdíl délek a také za vyšší teplotou „zvětšené“ tloušťky pásků
\[l_0\,(\alpha_{Zn}-\alpha_{Cu})\Delta t=\frac{1}{2}[d(1+\alpha_{Cu}\Delta t)+d(1+\alpha_{Zn}\Delta t)]\varphi \] \[l_0\,(\alpha_{Zn}-\alpha_{Cu})\Delta t=\frac{1}{2}d[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t)]\varphi \]Z této rovnice můžeme vyjádřit neznámý úhel:
\[\varphi=\frac{2l_o(\alpha_{Zn}-\alpha_{Cu})\Delta t}{d[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t)]}\]Pro délku zahřátého měděného pásku platí
\[l_o(1+\alpha_{Cu}\Delta t)=r\varphi\]Odsud vyjádříme hledaný poloměr r a dosadíme vyjádření úhlu φ:
\[r=\frac{l_o(1+\alpha_{Cu}\Delta t)}{\varphi}=\frac{l_o(1+\alpha_{Cu}\Delta t)}{\frac{2l_o(\alpha_{Zn}-\alpha_{Cu})\Delta t}{d[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t)]}}\] \[r=\frac{(1+\alpha_{Cu}\Delta t)[2+(\alpha_{Cu}+\alpha_{Zn})\Delta t]}{2(\alpha_{Zn}-\alpha_{Cu})\Delta t}\,d\]Dosadíme zadané hodnoty:
\[r=\frac{(1+17\cdot{10^{-6}}\cdot{80})[2+(30\cdot{10^{-6}}+17\cdot{10^{-6}})\cdot80]}{2\cdot(30\cdot{10^{-6}}-17\cdot{10^{-6}})\cdot80}\cdot{10^{-3}}\,\mathrm{m}\] \[r\dot{=}0{,}9647\,\mathrm{m}\dot{=}96\,\mathrm{cm}\]Poznámka: Pokud se podíváme podrobněji na obě závorky v čitateli výsledného zlomku, je patrné, že v nich můžeme zanedbat členy obsahující teplotní součinitele αZn a αCu. První závorka souvisí se změnou délky jednoho pásku a druhá závorka se změnou tloušťky pásku. Naopak v závorce ve jmenovateli žádné zanedbání udělat nemůžeme, protože oba členy mají podobnou velikost. Tato závorka vyjadřuje rozdíl v délkové roztažnosti obou kovů. Tím dostaneme jednodušší vztah:
\[r\dot{=}\frac{(1+...)[2+...]}{2(\alpha_{Zn}-\alpha_{Cu})\Delta t}\,d=\frac{d}{(\alpha_{Zn}-\alpha_{Cu})\Delta t}\] \[r\dot{=}\frac{10^{-3}}{(30\cdot{10^{-6}}-17\cdot{10^{-6}})\cdot{80}}\,\mathrm{m}\dot{=}0{,}9615\,\mathrm{m}\dot{=}96\,\mathrm{cm}\]Odpověď
Rozdíl v délkách obou pásků bude asi 0,2 mm a bimetal se ohne do oblouku s poloměrem přibližně 96 cm.Odkaz na pokus
Pokus Bimetal ukazuje, jak se chová bimetal při změně teploty.




