Sbírka řešených úloh

Důlní výtah

Úloha číslo: 369

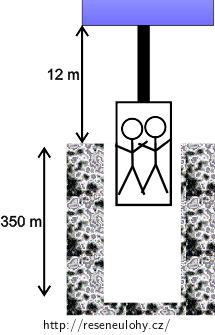
• Obrázek výtahu v důlní šachtě

  

• Zápis

  d = 2,5 cm = 0,025 m	průměr lana
  m = 650 kg	hmotnost kabiny a lidí
  h1 = 12 m	vzdálenost povrchu od motoru výtahu
  h2 = 350 m	hloubka šachty
  Δl1 = ?	prodloužení lana v případě a)
  Δl2 = ?	prodloužení lana v případě b)

  Další potřebné hodnoty:

  g = 9,81 ms−2	tíhové zrychlení
  E = 210 GPa = 2,1×1011 Pa	modul pružnosti oceli v tahu
  σE = 400 MPa = 4×108 Pa	mez pružnosti oceli

• Rozbor

  Jestliže na lano působí kabina svoji tíhou, lano napíná a to se bude pod vlivem této síly prodlužovat. Pokud tato síla nebude příliš velká, tak prodloužení bude úměrné působící síle, a pokud síla přestane působit, tak se lano vrátí na svoji původní délku. Aby toto platilo, nesmí normálové napětí (podíl mezi velikostí působící síly a obsahem průřezu materiálu) překročit mez pružnosti. Jedná se o tzv. pružnou deformaci, která je popsána Hookovým zákonem. V něm vystupuje modul pružnosti daného materiálu, což je konstanta úměrnosti mezi relativním prodloužením a normálovým napětím, které v materiálu vytváří působící síla.

• Řešení

  Na lano působí kabina svojí tíhou, která je stejně velká jako tíhová síla působící na kabinu \(F_G=mg\). Tato síla vytváří v lanu normálové napětí σ:

  \[\sigma = \frac {F_G}{S} = \frac{ mg}{ \pi \frac {d^2}{4}} = \frac{4mg}{\pi d^2} = \frac{4\cdot{650} \cdot{9{,}81}}{\pi \cdot{0{,}025^2}} \,\mathrm {Pa}\, \dot=\, 13\cdot{10^6} \,\mathrm {Pa} = 13 \,\mathrm {MPa}\]

  Vidíme, že působící normálové napětí je menší než mez pružnosti oceli \(\sigma_E=400\,\mathrm{MPa}\), a proto pro výpočet prodloužení lana můžeme použít Hookův zákon:

  \[\sigma = E \varepsilon ,\]

  kde E je modul pružnosti oceli v tahu a ε je relativní prodloužení lana, pro které platí:

  \[ \varepsilon = \frac {\Delta l}{l}.\]

  Dosadíme za normálové napětí σ a relativní prodloužení ε do Hookova zákona a vyjádříme prodloužení lana Δl:

  \[ \frac {4mg}{\pi d^2}=E \frac {\Delta l}{l} \Rightarrow \Delta l = \frac {4mgl}{\pi d^2 E}.\]

  Dosadíme zadané hodnoty. Přičemž za délku lana l dosadíme v případě, že je výtah na povrchu, vzdálenost motoru od povrchu h₁ a dostaneme:

  \[ \Delta l = \frac {4mgl}{\pi d^2 E}= \frac{4 \cdot {650} \cdot{9{,}81} \cdot{12}}{\pi \cdot{0{,}025^2} \cdot 2{,}1 \cdot{10^{11}}} \,\mathrm m \,\dot=\, 7{,}4\cdot{10^{-4}} \,\mathrm m = 0{,}74 \,\mathrm {mm}.\]

  V případě výtahu u dna šachty je délka lana l rovna součtu hloubky šachty h₂ a výšky motoru nad povrchem h₁, takže:

  \[ \Delta l = \frac {4mg(h_1 + h_2)}{\pi d^2 E}= \frac{4 \cdot{650} \cdot{9{,}81} \cdot{(12+350)}}{\pi \cdot{0{,}025^2} \cdot{2{,}1} \cdot{10^{11}}} \,\mathrm m \,\dot=\, 0{,}022 \,\mathrm m =2{,}2 \,\mathrm {cm}.\]

• Odpověď

  Jestliže je výtah na povrchu, tak se lano prodlouží asi o 0,74 mm. Pokud výtah sjede ke dnu šachty, je prodloužení lana rovno přibližně 2,2 cm.