Skleněná trubička a mýdlové bubliny
Úloha číslo: 1864
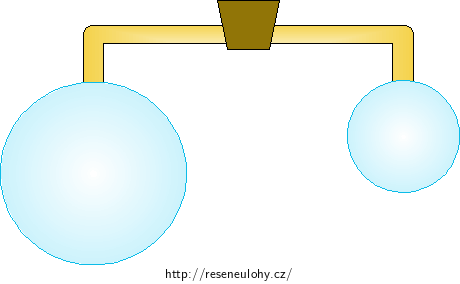
Na koncích skleněné trubičky vyfoukneme dvě mýdlové bubliny o různých poloměrech r < R. Pak otevřeme kohout a obě bubliny propojíme. Předpokládejme, že bubliny neprasknou. Budou se nějak měnit jejich poloměry?
Nápověda - Výpočet kapilárního tlaku
K vyřešení úlohy budete potřebovat vědět, jak závisí kapilární tlak uvnitř bubliny na jejím poloměru. Představte si, že se objem bubliny o maličko zmenší, tím bude menší i její poloměr a plocha povrchu. Vyjádřete si pomocí kapilárního tlaku práci, kterou vykonají povrchové síly při změně objemu bubliny, a také si napište, jak se změní povrchová energie bubliny. Rozmyslete si, v jakém vztahu je vykonaná práce a změna povrchové energie.
Kapilární tlak
V úzkých trubicích, při stěnách nádoby nebo u kapek a mýdlových bublin se setkáváme se zakřiveným povrchem kapaliny. V těchto případech vzniká vlivem povrchového napětí přídavný tlak, který je v každém místě kolmý k povrchu. Tento tlak nazýváme kapilární a značíme ho pk.
Rozbor
To, zda se budou nějak měnit poloměry bublin, bude záležet na tlaku vzduchu, který je uvnitř. Bude-li v jedné bublině tlak vyšší, začne vzduch z ní proudit do druhé bubliny.
Tlak uvnitř bubliny je dán atmosférickým tlakem vzduchu a tlakem syté páry, která se odpařuje z povrchu blány. Tyto tlaky jsou u obou bublin stejné. Dále se přidává tlak, který vzniká působením pružné blány bubliny, která vzduch uvnitř stlačuje. Tomuto tlaku říkáme kapilární tlak a musíme zjistit, jak závisí na poloměru bubliny.
Při odvození vztahu pro kapilární tlak vyjdeme z úvahy, že bublina trochu zmenší svůj poloměr, tím tedy i plochu povrchu a objem. Práci, kterou přitom vykonají síly povrchového napětí, vyjádříme jednak pomocí změny povrchové energie bubliny a také pomocí kapilárního tlaku a změny objemu.
Řešení část 1 - Výpočet kapilárního tlaku
Představme si, že objem bubliny se o maličko zmenší, tím bude menší i její poloměr a plocha povrchu. Změnu objemu označíme ΔV, změnu poloměru Δr a změnu povrchu plochy ΔS.
Povrchové síly při změně objemu bubliny vykonají práci, kterou můžeme vyjádřit pomocí kapilárního tlaku a změny objemu bubliny vztahem:
\[ΔW = {p_{\mathrm{k}}ΔV},\]Změní-li se objem bubliny, změní se také plocha povrchu a tím i její povrchová energie E. Změnu povrchové energie můžeme vyjádřit vztahem:
\[ΔE = {σΔS},\]kde σ je povrchové napětí a ΔS je změna povrchu bubliny.
Práce povrchových sil při změně objemu bubliny je rovna změně povrchové energie a platí tedy:
\[{σΔS} = {p_{\mathrm{k}}ΔV}.\]Z tohoto vztahu už můžeme vyjádřit kapilární tlak
\[{p_{\mathrm{k}}} = \frac{σΔS}{ΔV}.\tag{1}\]Řešení část 2 - Vyjádření ΔS a ΔV
Bublina má tvar koule. Pro objem koule o poloměru r platí vztah:
\[V = \frac{4}{3}πr^{3}\]Zvětší-li se poloměr koule o Δr, zvětší se její objem o ΔV. Změnu objemu vypočítáme jako rozdíl objemů zvětšené bubliny (která má poloměr r+Δr) a původní bubliny o poloměru r:
\[ΔV = \frac{4}{3}π(r+Δr)^{3} - \frac{4}{3}πr^{3}\]Po upravení získáme:
\[ΔV = \frac{4}{3}π(3r^{2}Δr + 3rΔr^{2} + Δr^{3}).\]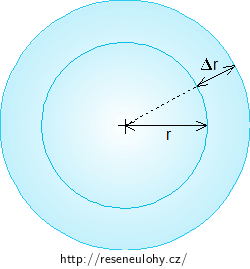
Protože se ale koule zvětšila jen o malý kousek, je změna poloměru Δr velmi malé číslo, jehož umocněním získáme ještě menší číslo. Druhou a třetí mocninu Δr tedy zanedbáme a získáme tak jednodušší vztah pro změnu objemu:
\[ΔV = 4πr^{2}Δr.\tag{2}\]Nyní si určíme změnu plochy povrchu bubliny. Bublinu tvoří velmi tenká kulová plocha mýdlové vody, uvnitř které je vzduch. Bublina má tedy dva povrchy - vnější a vnitřní, které jsou díky tenké vrstvičce mýdlové bubliny přibližně stejně velké.
Plocha povrchu bubliny je rovna dvojnásobku plochy povrchu koule (bublina má vnější a vnitřní povrch), platí tedy vztah:
\[ΔS = 2·4πr^{2}.\]Jestliže se poloměr bubliny zvětšil o Δr, změnu plochy povrchu ΔS vypočítáme jako rozdíl ploch povrchů zvětšené bubliny s poloměrem r+Δr a původní bubliny s poloměrem r:
\[ΔS = 8π(r+Δr)^{2} - 8πr^{2}.\]Po úpravě dostaneme:
\[ΔS = 8π(2rΔr + Δr^{2}).\]Druhou mocninu Δr opět zanedbáme, jelikož jde o velmi malé číslo, a dostaneme vztah pro změnu plochy povrchu bubliny:
\[ΔS = 16πrΔr.\tag{3}\]Komentář - vyjádření ΔS a ΔV s využitím diferenciálního počtu
Změnu objemu a plochy povrchu při malé změně poloměru bubliny můžeme také určit jako diferenciály.
Zderivujeme-li objem koule V podle r, dostaneme změnu objemu při malé změně poloměru
\[\frac{dV}{dr} = \frac{d}{dr}(\frac{4}{3}πr^{3}) = \frac{4}{3}π·3r^{2}\] \[dV = 4πr^{2} dr.\]Stejným způsobem zjistíme, jak se změní plocha povrchu bubliny při změně jejího poloměru. Nesmíme zapomenout, že bublina má dva povrchy
\[\frac{dS}{dr} = \frac{d}{dr}(8πr^{2}) = 8π·2r\] \[dS = 16πr dr.\]Porovnáme-li hodnoty dV a dS se vztahy (2) a (3), vidíme, že se shodují. Pokud bychom tedy příklad počítali s využitím diferenciálů, dostali bychom stejný výsledek.
Řešení část 3 - Výpočet kapilárního tlaku
Co se stane po propojení bublin?
V našem experimentu máme dvě bubliny, velkou a malou. Ze vztahu (4) vyplývá, že kapilární tlak je nepřímo úměrný poloměru bubliny, tedy čím menší je bublina, tím větší je tlak v této bublině. Po propojení obou bublin začne vzduch z menší bubliny vlivem vyššího tlaku proudit do větší bubliny. Bublina s větším poloměrem se tedy začne zvětšovat a menší bublina postupně zanikne.
Poznámka: Pokus k této úloze najdete zde: Mýdlové bubliny propojené trubičkou.




