Reciproká mříž ke kubickým centrovaným mřížím
Úloha číslo: 2278
Ukažte, že reciprokou mříží ke kubické prostorově centrované mříži je kubická plošně centrovaná mříž. Jaký je její mřížový parametr?
Jaká mříž bude reciproká ke kubické plošně centrované mříži a jaký bude její mřížový parametr?
Rozbor
Pokud známe translační vektory přímé mříže \(\overrightarrow{a_1}, \overrightarrow{a_2}, \overrightarrow{a_3}\), můžeme translační vektory reciproké mříže \(\overrightarrow{b_1}, \overrightarrow{b_2}, \overrightarrow{b_3}\) spočítat z následujících vztahů:
\[\overrightarrow{b_1}=\frac{2\pi}{V}(\overrightarrow{a_2} \times \overrightarrow{a_3}),\] \[\overrightarrow{b_2}=\frac{2\pi}{V}(\overrightarrow{a_3} \times \overrightarrow{a_1}),\] \[\overrightarrow{b_3}=\frac{2\pi}{V}(\overrightarrow{a_1} \times \overrightarrow{a_2}),\] kde \(V\) je objem buňky dané translačními vektory \(\overrightarrow{a_1}, \overrightarrow{a_2}, \overrightarrow{a_3}\): \[V=\overrightarrow{a_1} \cdot (\overrightarrow{a_2} \times \overrightarrow{a_3}).\] Je tedy třeba si vhodně zvolit translační vektory kubické prostorově centrované mříže, spočítat translační vektory reciproké mříže podle výše uvedených vztahů a identifikovat tyto vektory s translačními vektory kubické plošně centrované mříže.Nápověda: Translační vektory
Je třeba si vhodně zvolit translační vektory pro oba dva typy mřížek.
Řešení: Reciproká mříž ke kubické prostorově centrované mříži
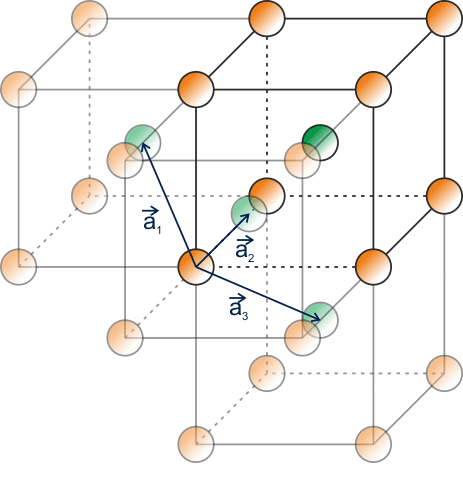
Jak je podrobněji rozebráno výše, pokud má konvenční buňka kubické prostorově centrované mříže mřížový parametr \(a\), můžeme si translační vektory vyjádřit následujícím způsobem:
\[\overrightarrow{a_1} = \frac{a}{2} (-1{,}1,1),\] \[\overrightarrow{a_2} = \frac{a}{2} (1,-1{,}1),\] \[\overrightarrow{a_3} = \frac{a}{2} (1{,}1,-1).\]Vyjádříme si objem buňky dané těmito translačními vektory:
\[V=\overrightarrow{a_1} \cdot (\overrightarrow{a_2} \times \overrightarrow{a_3})= \frac{a}{2} (-1{,}1,1) \cdot \frac{a^2}{2}(0, 2, 2)=0+\frac{a^3}{4}+\frac{a^3}{4}=\frac{a^3}{2}.\]Translační vektory reciproké mříže poté vypočteme ze známých vztahů:
\[\overrightarrow{b_1}=\frac{2\pi}{V}(\overrightarrow{a_2} \times \overrightarrow{a_3})= \frac{a^2}{2} (0{,}1,1) \cdot \frac{4\pi}{a^3}=\frac{2\pi}{a} (0{,}1,1),\] \[\overrightarrow{b_2}=\frac{2\pi}{V}(\overrightarrow{a_3} \times \overrightarrow{a_1})= \frac{a^2}{2} (1{,}0,1) \cdot \frac{4\pi}{a^3}=\frac{2\pi}{a} (1{,}0,1),\] \[\overrightarrow{b_3}=\frac{2\pi}{V}(\overrightarrow{a_1} \times \overrightarrow{a_2})= \frac{a^2}{2} (1{,}1,0) \cdot \frac{4\pi}{a^3}=\frac{2\pi}{a} (1{,}1,0).\] Tyto vektory jsou translačními vektory kubické plošně centrované mříže s mřížovým parametrem \(4\pi/a\).Řešení: Reciproká mříž ke kubické plošně centrované mříži
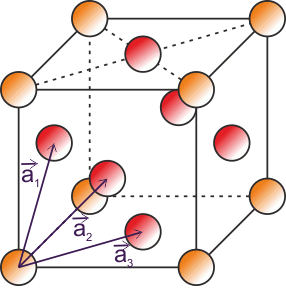
Jak jsme viděli v předchozím bodě, translační vektory kubické plošně centrované mříže můžeme psát ve tvaru
\[\overrightarrow{a_1}=\frac{a}{2} (0{,}1,1),\] \[\overrightarrow{a_2}=\frac{a}{2} (1{,}0,1),\] \[\overrightarrow{a_3}=\frac{a}{2} (1{,}1,0).\]Opět si vyjádříme napřed objem buňky dané těmito translačními vektory:
\[V=\overrightarrow{a_1} \cdot (\overrightarrow{a_2} \times \overrightarrow{a_3})= \frac{a}{2} (0{,}1,1) \cdot ( \frac{a}{2} (1{,}0,1) \times \frac{a}{2} (1{,}1,0) )= \frac{a}{2} (0{,}1,1) \cdot \frac{a^2}{4}(-1, 1, 1)=\frac{a^3}{8}(0+1+1)=\frac{a^3}{4}.\]Translační vektory reciproké mříže poté vypočteme ze známých vztahů:
\[\overrightarrow{b_1}=\frac{2\pi}{V}(\overrightarrow{a_2} \times \overrightarrow{a_3})= 2\pi\cdot \frac{a^2}{4} (-1{,}1,1) \cdot \frac{4}{a^3}=\frac{2\pi}{a} (-1{,}1,1),\] \[\overrightarrow{b_2}=\frac{2\pi}{V}(\overrightarrow{a_3} \times \overrightarrow{a_1})= 2\pi\cdot \frac{a^2}{4} (1,-1{,}1) \cdot \frac{4}{a^3}=\frac{2\pi}{a} (1,-1{,}1),\] \[\overrightarrow{b_3}=\frac{2\pi}{V}(\overrightarrow{a_1} \times \overrightarrow{a_2})= 2\pi\cdot \frac{a^2}{4} (1{,}1,-1) \cdot \frac{4}{a^3}=\frac{2\pi}{a} (1{,}1,-1).\] Tyto vektory jsou translačními vektory kubické prostorově centrované mříže s mřížovým parametrem \(4\pi/a\).Odpověď
Reciprokou mříží ke kubické prostorově centrované mříži o mřížovém parametru \(a\) je kubická plošně centrovaná mříž o mřížovém parametru \(4\pi/a\).
Reciprokou mříží ke kubické plošně centrované mříži o mřížovém parametru \(a\) je kubická prostorově centrovaná mříž o mřížovém parametru \(4\pi/a\).
Poznámka ke značení a definici vektorů reciproké mříže
V této sbírce značíme vektory přímé mříže jako \(\overrightarrow{a_1}, \overrightarrow{a_2}, \overrightarrow{a_3}\) a vektory reciproké mříže \(\overrightarrow{b_1}, \overrightarrow{b_2}, \overrightarrow{b_3}\). Lze se setkat i s jinými konvencemi, například vektory přímé mříže mohou být značeny \(\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}\) a vektory reciproké mříže se mohou označovat \(\overrightarrow{a^*}, \overrightarrow{b^*}, \overrightarrow{c^*}\).
Rovněž definujeme vektory reciproké mříže těmito vztahy:
\[\overrightarrow{b_1}=\frac{2\pi}{V}(\overrightarrow{a_2} \times \overrightarrow{a_3}),\] \[\overrightarrow{b_2}=\frac{2\pi}{V}(\overrightarrow{a_3} \times \overrightarrow{a_1}),\] \[\overrightarrow{b_3}=\frac{2\pi}{V}(\overrightarrow{a_1} \times \overrightarrow{a_2}).\]Jindy se používá odlišná konvence, kdy se vektory reciproké mříže definují takto:
\[\overrightarrow{b_1}=\frac{1}{V}(\overrightarrow{a_2} \times \overrightarrow{a_3}),\] \[\overrightarrow{b_2}=\frac{1}{V}(\overrightarrow{a_3} \times \overrightarrow{a_1}),\] \[\overrightarrow{b_3}=\frac{1}{V}(\overrightarrow{a_1} \times \overrightarrow{a_2}).\]