Vratný kruhový děj
Úloha číslo: 430
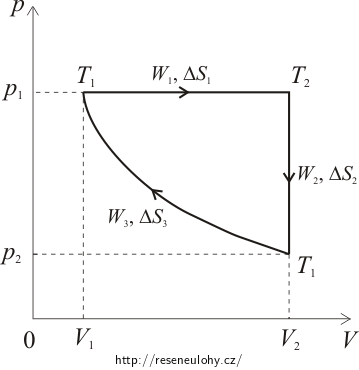
Určete celkovou práci, změnu entropie a účinnost u vratného kruhového děje skládajícího se z izobarické expanze, izochorického ochlazení a izotermické komprese. Srovnejte účinnost tohoto cyklu s účinností ideálního Carnotova cyklu, pracují-li oba mezi teplotami 300 K a 1000 K.
Předpokládejte, že plyn je ideální, dvouatomový a že jeho látkové množství je 1 mol.
Zápis
T1 = 300 K teplota jedné lázně T2 = 1000 K teplota druhé lázně n = 1 mol látkové množství plynu W = ? celková práce ΔS = ? změna entropie η = ? účinnost ηid = ? účinnost ideálního Carnotova cyklu Z tabulek:
R = 8,31 JK−1mol−1 molární plynová konstanta Nápověda 1 – celková práce
Celková práce W je rovna součtu prací vykonaných plynem v jednotlivých částech cyklu.
Rozmyslete si, jak hodnoty těchto prací určit.
Nápověda 2
K vyjádření neznámých objemů V1, V2 a tlaků p1, p2 použijte stavovou rovnici ideálního plynu.
Rozbor – celková práce
Při výpočtu celkové práce musíme uvážit, kdy koná práci samotný plyn a kdy okolí.
Při izobarické expanzi koná plyn práci, kterou určíme jako součin tlaku a změny objemu. V průběhu izochorického děje se objem plynu nemění, systém tedy nekoná práci. Při izotermické kompresi koná práci okolí. Protože během tohoto děje není tlak konstantní, musíme pro výpočet práce použít integrální počet.
Pro vyjádření tlaku jako funkci objemu použijeme tzv. Boyle-Mariottův zákon.
Řešení – celková práce
Při výpočtu celkové práce W musíme uvážit, kdy koná práci samotný plyn a kdy okolí.
Při izobarické expanzi plyn zvětšuje svůj objem a při tom vykoná práci W1. Pro tu platí vztah
\[W_1=p_1\left(V_2-V_1\right),\]kde p1 je tlak plynu a V1 a V2 jeho objem před a po expanzi.
V průběhu izochorického děje se objem plynu nemění, systém tedy nekoná práci a platí
\[W_2=0.\]Při izotermické kompresi je plyn stlačován. Jeho práce W3 je tudíž záporná (práci koná okolí). Protože při izotermickém ději není tlak p plynu konstantní, musíme pro výpočet práce použít integrální počet:
\[W_3 = \int\limits_{V_2}^{V_1}p\, \text{d}V,\]kde V2 je objem plynu před kompresí a V1 jeho objem po kompresi.
Tlak p jako funkci objemu V vyjádříme z tzv. Boyle-Mariottova zákona, podle něhož platí:
\[p_2V_2 = pV. \]Dostaneme
\[p = \frac{p_2V_2}{V}\]a můžeme přejít k samotné integraci
\[W_3 = \int\limits_{V_2}^{V_1}p\, \text{d}V = \int\limits_{V_2}^{V_1}\frac{p_2V_2}{V}\, \text{d}V =\]vytkneme konstanty před integrál
\[=p_2V_2 \int\limits_{V_2}^{V_1}\frac{1}{V}\, \text{d}V = \]zintegrujeme a dosadíme meze
\[=p_2V_2[\ln{V}]_{V_2}^{V_1} = p_2V_2\ln{\frac{V_1}{V_2}}.\]Pro celkovou práci W cyklu potom bude platit vztah
\[W=W_1+W_3=p_1\left(V_2-V_1\right)+p_2V_2\ln{\frac{V_1}{V_2}}.\]Hodnoty příslušných tlaků a objemů však neznáme. K jejich určení použijeme stavovou rovnici ideálního plynu
\[pV=nRT\]a vztah
\[\frac{V_1}{V_2}=\frac{T_1}{T_2}\]plynoucí z faktu, že pro izobarický děj je podíl objemu a teploty konstantní (Gay-Lussacův zákon).
Díky tomu můžeme pro celkovou práci psát
\[W=nR\left(T_2-T_1\right)+nRT_1\ln{\frac{T_1}{T_2}}\]a po úpravě
\[W= nR\left[T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)\right].\]Nápověda 3 – změna entropie
Pro určení změny entropie ΔS musíte nejprve vypočítat teplo, které plyn přijímá, resp. odevzdává v jednotlivých částech cyklu.
Rozmyslete si, co pro tato tepla platí.
Rozbor – změna entropie
Nejprve vypočítáme tepla a s nimi související změny entropie v jednotlivých částech cyklu. Při tom si musíme uvědomit, kdy plyn teplo přijímá (entropie roste) a kdy jej odevzdává (entropie klesá).
Při izobarické expanzi se zvyšuje teplota a plyn navíc koná práci. Z 1. termodynamického zákona tudíž plyne, že teplo je plynem přijímáno. Při výpočtu příslušné změny entropie musíme použít integrální počet, protože teplota se v průběhu tohoto děje mění.
Při izochorickém ochlazení systém nekoná práci a klesá vnitřní energie plynu. To znamená, že při tomto ději odevzdá plyn teplo svému okolí. Protože ani při tomto ději není teplota konstantní, musíme pro výpočet změny entropie opět použít integrální počet.
Při izotermické kompresi koná práci okolí. Vnitřní energie plynu přitom neroste. Podle 1. termodynamického zákona proto musí docházet k tomu, že plyn teplo odevzdává. Entropie tedy klesá. Protože je v průběhu tohoto děje teplota konstantní, můžeme stanovit změnu entropie jako podíl odevzdaného tepla a teploty, při níž děj probíhá.
Řešení – změna entropie
Nyní budeme počítat tepla Qi a s nimi související změny entropie ΔSi v jednotlivých částech cyklu. Při tom si musíme uvědomit, kdy plyn teplo přijímá a kdy jej odevzdává.
Při izobarické expanzi se zvyšuje teplota a plyn navíc koná práci. Z 1. termodynamického zákona tudíž plyne, že teplo Q1 je plynem přijímáno. Platí pro něj vztah
\[Q_1=C_pn\left(T_2-T_1\right),\]kde Cp je molární tepelná kapacita při stálém tlaku, n látkové množství a T1, T2 počáteční a koncová teplota.
Připomeňme si, že pro molární tepelnou kapacitu při stálém objemu CV platí u dvouatomového plynu vztah
\[C_V=\frac{5}{2}R,\]kde R je molární plynová konstanta.
Užitím Meyerova vztahu Cp = CV + R tak okamžitě pro molární tepelnou kapacitu za stálého tlaku dostáváme:
\[C_p=\frac{5}{2}R+R=\frac{7}{2}R.\]Pro teplo Q1 dodané plynu tedy platí
\[Q_1=\frac{7}{2}nR\left(T_2-T_1\right).\]Nyní můžeme určit změnu entropie ΔS1 při tomto ději. Musíme si uvědomit, že teplota T v jeho průběhu není konstantní, a proto nelze spočítat změnu entropie jako podíl celkového tepla Q1 a teploty. Musíme použít integrální počet.
Pro elementární změnu entropie dS1 platí
\[\text{d}S_1=\frac{\text{d}Q_1}{T}=\frac{7nR\,\text{d}T}{2T}. \]Celkovou změnu entropie ΔS1 pak dostaneme integrací tohoto výrazu v mezích od T1 do T2
\[ \Delta S_1= \int\limits_{T_1}^{T_2}\,\text{d}S_1 =\int\limits_{T_1}^{T_2}\frac{7}{2}\frac{nR}{T}\,\text{d}T = \]vytkneme konstanty před integrál
\[=\frac{7}{2}nR\int\limits_{T_1}^{T_2}\frac{\text{d}T}{T}= \]zintegrujeme a dosadíme meze
\[=\frac{7}{2}nR\left[\ln{T}\right]_{T_1}^{T_2} = \frac{7}{2}nR\ln{\frac{T_2}{T_1}}.\]Při izochorickém ochlazení systém nekoná práci a klesá vnitřní energie plynu. To znamená, že při tomto ději odevzdá plyn svému okolí teplo Q2, pro které platí
\[Q_2=C_Vn\left(T_1-T_2\right)=\frac{5}{2}nR\left(T_1-T_2\right).\]Protože ani při tomto ději teplota není konstantní, napíšeme si výraz pro elementární změnu entropie dS2 a následně ho zintegrujeme v mezích od T2 do T1. Pro změnu entropie ΔS2 tedy platí:
\[ \Delta S_2= \int\limits_{T_2}^{T_1}\,\text{d}S_2 =\int\limits_{T_2}^{T_1}\frac{5}{2}\frac{nR}{T}\,\text{d}T = \]vytkneme konstanty před integrál
\[=\frac{5}{2}nR\int\limits_{T_2}^{T_1}\frac{\text{d}T}{T}= \]zintegrujeme a dosadíme meze
\[=\frac{5}{2}nR\left[\ln{T}\right]_{T_2}^{T_1} = \frac{5}{2}nR\ln{\frac{T_1}{T_2}} = -\frac{5}{2}nR\ln{\frac{T_2}{T_1}}.\]Změna entropie vyšla záporná, protože plyn teplo odevzdával.
Nyní určíme změnu entropie ΔS3 při izotermické kompresi. Jak jsme uvedli již v první části příkladu, při tomto ději koná práci okolí. Vnitřní energie plynu přitom neroste. Podle 1. termodynamického zákona proto musí docházet k tomu, že plyn teplo Q3 odevzdává, proto změna entropie vyjde opět záporná. Entropie tedy klesá. Protože je v průběhu tohoto děje teplota konstantně rovna T1, můžeme stanovit změnu entropie ΔS3 užitím vztahu
\[\Delta S_3=\frac{Q_3}{T_1}.\]Pro izotermické procesy podle 1. termodynamického zákona platí, že odevzdané teplo je stejné jako dodaná práce. Pro ΔS3 tak dostaneme:
\[\Delta S_3=\frac{Q_3}{T_1}=\frac{W_3}{T_1} = \frac{nRT_1\ln{\frac{T_1}{T_2}}}{T_1} = nR\ln{\frac{T_1}{T_2}} = -nR\ln{\frac{T_1}{T_2}}.\]Nyní již můžeme určit celkovou změnu entropie ΔS za celý cyklus. Platí
\[\Delta S=\Delta S_1+\Delta S_2+\Delta S_3\] \[\Delta S=\frac{7}{2}nR\ln{\frac{T_2}{T_1}} - \frac{5}{2}nR\ln{\frac{T_2}{T_1}} - nR\ln{\frac{T_2}{T_1}}=0.\]To znamená, že změna entropie za celý cyklus je nulová. Tento závěr jsme ale mohli udělat rovnou bez zdlouhavých výpočtů, protože entropie je stavová veličina. Jestliže se plyn po vykonání jednoho cyklu vrátí do původního stavu, musí mít i stejnou entropii a její změna je tedy nulová. Výpočtem jsme tuto skutečnost ověřili.
Nápověda 4 – účinnost
Připomeňte si, jak je definována účinnost tepelného stroje (obecně) a účinnost Carnotova stroje.
Rozbor – účinnosti η a ηid
Napíšeme si vztah pro účinnost tepelného cyklu (obecně) a pro Carnotův cyklus. Výsledné hodnoty pak porovnáme.
Účinnost Carnotova cyklu by měla vyjít větší. To je v souladu s tím, že Carnotův ideální kruhový děj má pro dané teploty ohřívače a chladiče maximální možnou účinnost.
Řešení – účinnosti η a ηid
Účinnost η je definována jako podíl celkové práce W vykonané během cyklu a tepla Qdod dodaného plynu, tedy
\[\eta=\frac{W}{Q_{dod}}.\]Práci W již máme spočítánu. Protože plyn přijímá teplo jen během izobarické expanze, platí Qdod = Q1.
Pro účinnost tedy dostáváme
\[\eta=\frac{W}{Q_1} = \frac{nR\left[T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)\right]}{\frac{7}{2}nR\left(T_2-T_1\right)} = \frac{T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)}{\frac{7}{2}\left(T_2-T_1\right)}.\]Nyní ještě pro srovnání určíme účinnost ηid ideálního Carnotova cyklu pracujícího mezi stejnými teplotami. Platí pro ni vztah
\[\eta_{id}=\frac{T_2-T_1}{T_2}.\]Číselné dosazení
Celková vykonaná práce:
\[W= nR\left[T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)\right]\] \[W= 1\cdot{ 8{,}31}\cdot \left[1000-300\cdot \left(1-\ln{\frac{300}{1000}}\right)\right]\,\mathrm{J}\dot{=}2815\,\mathrm{J}\dot{=}2{,}8\,\mathrm{kJ}\]Účinnost zadaného kruhového děje:
\[\eta= \frac{T_2-T_1\left(1-\ln{\frac{T_1}{T_2}}\right)}{\frac{7}{2}\left(T_2-T_1\right)}\] \[\eta = \frac{1000-300\cdot \left(1-\ln{\frac{300}{1000}}\right)}{\frac{7}{2}\cdot \left(1000-300\right)}\dot{=}0{,}14\]Účinnost ideálního Carnotova cyklu:
\[\eta_{id}=\frac{T_2-T_1}{T_2}\] \[\eta_{id}=\frac{1000-300}{1000}=0{,}7\]Vidíme, že Carnotův cyklus pracující mezi stejnými teplotami by měl mnohem větší účinnost než námi uvažovaný cyklus. To je v souladu s tím, že Carnotův ideální kruhový děj má pro dané teploty ohřívače a chladiče maximální možnou účinnost.
Odpověď
Celková práce cyklu je přibližně 2,8 kJ.
Celková změna entropie za celý cyklus je rovna nule.
Účinnost cyklu je přibližně 0,14.
Účinnost Carnotova cyklu je 0,7.
pV-diagram