Napětí na okraji válce
Úloha číslo: 2157
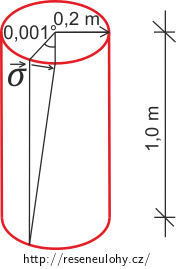
Je dán ocelový kolmý kruhový válec o poloměru 0,2 m a výšce 1 m, jehož spodní podstava je pevně vetknuta v zemi. Modul pružnosti ve smyku je 80 GPa. Jak velké je vodorovné napětí na okraji kolmého kruhového řezu válce, jestliže se horní podstava vzhedem ke spodní pootočí o úhel 0,001°?
Zápis
r = 0,2 m poloměr válce v = 1 m výška válce G = 80 GPa modul pružnosti ve smyku β = 0,001° úhel pootočení σ = ? napětí Rozbor
Průběh napětí je v každém kolmém průřezu stejný. Takže zde můžeme uvažovat napětí, které je tečné k plášti, například na okraji horní podstavy. Zde ze zadání plyne, že deformace můžeme uvažovat malé. Proto můžeme část pláště podél výšky aproximovat rovinným tenkým obdélníkem. Když si úhel smyku tohoto obdélníku vyjádříme vzhledem k napětí a také vzhledem k pootočení podstavy, pak porovnáním můžeme vyjádřit napětí v závislosti na pootočení.
Nápověda
Aproximujte si plochu pláště podél celé výšky dost tenkým rovinným obdélníkem a použijte vztah mezi úhlem smyku a tečným napětím působícím po stranách tohoto obdélníku. Pak už stačí tento úhel smyku vyjádřit pomocí úhlu pootočení podstavy za předpokladu malých deformací. To znamená použít vztah mezi úhlem a dost malou délkou kružnicového oblouku, kterou můžeme aproximovat úsečkou. Pak už jen stanovte vztah mezi napětím a úhlem pootočení a číselně dosaďte.
Řešení
Kvůli malé deformaci můžeme na plášti podél výšky uvažovat dost tenký obdélník (jak je znázorněno na obrázku), po jehož stranách bude působit právě hledané napětí.
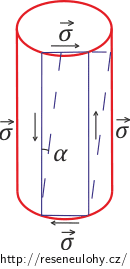
Tento obdélník se deformuje o úhel smyku α, který můžeme pomocí Hookova zákona vyjádřit vztahem:
\[\alpha\,=\,\frac{\sigma}{G}.\tag{1}\]Protože úkolem je určit napětí, tak (1) ještě přepíšeme na:
\[\sigma\,=\,\alpha G.\tag{2}\]V aproximaci můžeme délku l, o kterou se posune levý horní vrchol obdélníku, zapsat jako:
\[l\,=\,\alpha v.\tag{3}\]Ovšem při aproximaci dost malé délky kružnice úsečkou se o l posune i bod na okraji horní podstavy při pootočení o β. To se pokusí znázornit obrázek.
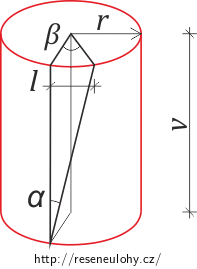
Podle předchozího tedy platí:
\[l\,=\,\beta r.\tag{4}\]Ze (3) a (4) dále vyjádříme úhel smyku:
\[\alpha\,=\,\beta\frac{r}{v}.\tag{5}\](5) dosadíme do (2):
\[\sigma\,=\,\beta G\frac{r}{v}.\tag{6}\]Protože v zadání je úhel pootočení zapsán ve stupňové míře a v řešení jsme používali obloukovou míru, je třeba úhel β ze zadání zapsat do obloukové míry vztahem:
\[\beta\,=\,0{,}001°\,=\,0{,}001\cdot\frac{\pi}{180} \mathrm{rad}\,=\,1{,}745{\cdot}10^{-5} \mathrm{rad}.\]Dále už číselně dosadíme do (6), takže vychází:
\[\sigma\,=\,1{,}745{\cdot}10^{-5}\cdot80{\cdot}10^{9}\frac{0{,}2}{1}\mathrm{Pa}\,=\,0{,}279\mathrm{MPa}.\]Odpověď
Napětí na okraji kolmého průřezu válce je:
\[\sigma\,=\,0{,}279\mathrm{MPa}.\]

