Výška hladiny kapaliny v kapiláře
Úloha číslo: 1910
V nádobě s vodou o teplotě 20° C jsou jedním koncem ponořeny dvě kapiláry s průměry 0,1 mm a 0,3 mm. Jak se změní vzdálenost hladin v kapilárách, ohřejeme-li vodu na 70° C?
Zápis
Zadané hodnoty:
r1 = 0,05 mm = 5·10−5 m poloměr první kapiláry r2 = 0,15 mm = 1,5·10−4 m poloměr druhé kapiláry Tabulkové hodnoty:
σ20 = 73·10−3 N m−1 povrchové napětí vody při 20 °C σ70 = 64·10−3 N m−1 povrchové napětí vody při 70 °C ρ20 = 998,2 kg m−3 hustota vody při 20 °C ρ70 = 977,8 kg m−3 hustota vody při 70 °C Rozbor
Nejprve je třeba zamyslet se nad tím, na čem závisí, do jaké výšky vystoupí voda v kapiláře. Ovlivní to jednak průměr kapiláry - v užší kapiláře vystoupí voda výše. Výška vystoupení vody závisí také na povrchovém napětí. Povrchové napětí vody se ale mění s teplotou - se vzrůstající teplotou klesá. Na teplotě závisí i hustota vody, která od cca 4 °C s rostoucí teplotou též klesá. Při zahřátí vody se tedy výška vody v kapilárách změní. Změnu průměru kapiláry při změně teploty vody nebudeme uvažovat.
Nejdříve určíme výšku hladiny vody v obou kapilárách při teplotě 20 °C. Poté určíme vzdálenost hladin v těchto kapilárách.
Obdobným způsobem pak určíme vzdálenost hladin vody v obou kapilárách při teplotě 70 °C.
Nakonec vypočítáme, jak se změní vzdálenost hladin v kapilárách při uvedené změně teploty .
Nápověda
Abyste mohli vypočítat změnu vzdálenosti hladin v kapilárách, potřebujete vědět, jaký vztah platí pro výpočet výšky hladiny kapaliny v kapiláře.
Hodnoty povrchového napětí vody při různých teplotách najdete v Tabulkách nebo na internetu.
Řešení
Nejdříve určíme vzdálenost hladin v kapilárách při teplotě vody 20° C.
Výšku hladiny vypočítáme podle vztahu (1). Povrchové napětí σ a hustota kapaliny ρ závisí na teplotě, proto budou mít tyto veličiny ve spodním indexu zapsanou teplotu kapaliny.
Označme si výšku hladiny vody v kapiláře o průměru 0,1 mm při teplotě 20° C jako h(1)20. Tuto výšku určíme ze vztahu
\[h^{(1)}_{20} = \frac{2σ_{20}}{r_{1}ρ_{20}g}.\tag{2}\]Pro výšku hladiny v kapiláře o průměru 0,3 mm při teplotě 20° C, kterou jsme označili jako h(2)20, platí
\[h^{(2)}_{20} = \frac{2σ_{20}}{r_{2}ρ_{20}g}.\tag{3}\]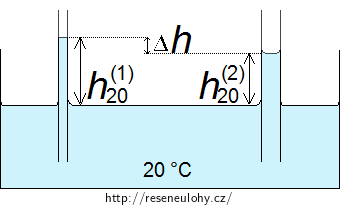
Vzdálenost hladin v obou kapilárách určíme jako rozdíl výšek hladin v užší (2) a širší (3) kapiláře
\[Δh_{20} = h^{(1)}_{20} − h^{(2)}_{20} = \frac{2σ_{20}}{ρ_{20}g}\left(\frac{1}{r_1} − \frac{1}{r_2}\right).\tag{4}\]Pro vzdálenost hladin v kapilárách při 70° C platí obdobný vztah, jako při 20° C
\[Δh_{70} = \frac{2σ_{70}}{ρ_{70}g}\left(\frac{1}{r_1} − \frac{1}{r_2}\right).\tag{5}\]Nyní můžeme určit změnu vzdáleností hladin v apilárách při změně teploty vody z 20° C (4) na 70° C (5)
\[Δh = Δh_{20} − Δh_{70} = \frac{2}{g}\left(\frac{σ_{20}}{ρ_{20}} − \frac{σ_{70}}{ρ_{70}}\right)\left(\frac{1}{r_1} − \frac{1}{r_2}\right).\tag{6}\]Číselné dosazení
Nyní dosadíme do vztahu (6) známé hodnoty a vypočítáme rozdíl vzdáleností hladin
\[Δh \dot{=}\, \frac{2}{9{,}8}\left(\frac{73·10^{−3}}{998{,}2} − \frac{64·10^{−3}}{977{,}8}\right)\left(\frac{1}{5·10^{−5}} − \frac{1}{1{,}5·10^{−4}}\right) m\] \[Δh \dot{=}\, 2{,}1·10^{−2} m. \]Odpověď
Vypočítali jsme, že vzdálenost hladin v kapilárách se při změně teploty z 20° C na 70° C změní přibližně o 2,1 cm.
Pokus k této úloze najdete zde: Výška hladiny kapaliny v kapiláře.




