Sbírka řešených úloh

Energetické ztráty parovodního potrubí

Úloha číslo: 500

• Nápověda

  Energetickými ztrátami se rozumí teplo, které unikne přes stěny potrubí ven.

• Rozbor

  Teplo, které projde stěnou za jednotku času je přímo úměrné rozdílu teplot a ploše, přes kterou prochází. To je v našem případě plášť válce o průměru potrubí a délce rovné délce potrubí. Dále je prošlé teplo nepřímo úměrné tloušťce materiálu, tj. tloušťce potrubí. Konstantou úměrnosti v tomto vztahu je zadaný součinitel tepelné vodivosti materiálu, ze kterého je potrubí vyrobeno.

  Vztah popisující prostup tepla materiálem se jmenuje rovnice vedení tepla.

• Zápis

  d = 60 cm = 0,6 m	průměr potrubí
  l = 1 km = 103 m	délka potrubí
  b = 1 cm = 0,01 m	tloušťka potrubí
  λ = 50 W m−1K−1	součinitel tepelné vodivosti užitého materiálu
  τ = 30 dní = 30·24·3600 s = 2,59·106 s	doba, za kterou se počítáme ztráty
  t1 = 17,8 °C → T1 = 290,95 °C	ustálená venkovní teplota
  T2 = 373 K	teplota páry
  Q = ?	tepelné ztráty

• Řešení

  

  Teplo, které prostoupí stěnou potrubí za jednotku času, je přímo úměrné ploše a rozdílu teplot, který je v našem případě konstantní, a nepřímo úměrné tloušťce stěny. Hlavním úkolem je tedy výpočet plochy, jíž teplo uniká.

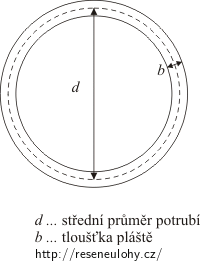
  Všimněme si, že průměr potrubí je podstatně větší než tloušťka pláště válce, a proto zadanou hodnotu 60 cm budeme považovat za střední průměr (správně bychom museli, jak je patrné z obrázku, rozlišit vnitřní a vnější průměr potrubí, pro výpočet by pak však bylo potřeba užít integrálního počtu). Proto můžeme plochu, jíž teplo uniká, pokládat za plášť válce, jehož výškou odpovídá délce potrubí l, a průměr válce je roven poté zadané hodnotě d.

  Pro plochu tedy pak můžeme psát:

  \[ S=2\pi rl = \pi dl \] kde r je polovina průměru d, tedy poloměr potrubí. Pro celkové energetické ztráty, když označíme tloušťku potrubí jako b, pak platí: \[Q=\frac{\lambda S\tau\mathrm{\Delta}t}{b}=\frac{\lambda\pi dl\tau\left(t_2-t_1\right)}{b}\,\mathrm{.}\]

  Číselné dosazení:

  \[Q=\frac{50\pi 0{,}6\cdot{10^3}\cdot{2{,}59}\cdot{10^6}\cdot\left(373-290{,}95\right)}{0{,}01}\,\mathrm{J}=\] \[Q\dot{=}2{,}0\cdot{10^{15}}\,\mathrm{J}=2\,000\,\mathrm{TJ}\]

• Odpověď

  Energetické ztráty potrubí za 30 dní jsou okolo 2 000 TJ.

• Pro zajímavost

  Parovodní potrubí mají ve skutečnosti ještě silnou izolační vrstvu, která brání rychlému ochlazování páry v potrubí.

  Pára v potrubí se pohybuje díky svému tlaku, který je další důležitou charakteristikou parovodů. Při přenosu páry potrubím je výhodné, aby byla pára nasycená, tj. nebyl v ní kondenzát. Nasycená párá má totiž při daném tlaku přesně definovanou teplotu, což je výhodné pro spotřebiče, kterým je pára dodávaná. Vzniklý kondenzát také ničí potrubí a snižuje jeho životnost.

  Během přenosu však pára ztrácí tlak i teplotu a na dně potrubí vzniká kondenzát, který je nutno odvádět. Proto má potrubí ještě po nějakých úsecích odvody tohoto kondenzátu.

  Pro co nejefektivnější přenos tepla je tedy potřeba, aby byly sníženy nejen tepelné ztráty dobrou tepelnou izolací, ale i ztráty tlaku vodní páry.