Změna vnitřní energie ideálního plynu
Úloha číslo: 407
Izochorickým dějem se původní tlak 100 kPa ideálního plynu o objemu 10 l zvětšil na čtyřnásobnou hodnotu. Následně tento plyn izobaricky ochladíme, přičemž se jeho objem sníží na polovinu.
Uvažujeme, že jde o jednoatomový ideální plyn s Poissonovou konstantou:
\[\kappa = \frac{5}{3}\]Určete práci vnějších sil, celkové teplo a změnu vnitřní energie plynu během popsaného procesu.
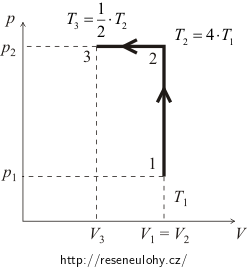
Obrázek
Nápověda
Rozmyslete si, jak lze z p-V diagramu určit práci.
Promyslete si, jak se mění teplota ideálního plynu při izochorickém zvýšení tlaku a při izobarickém snížení objemu.
Rozbor
Celková práce vykonaná vnějšími silami je rovna práci vykonané při izobarickém ději, protože při izochorickém ději se práce nekoná. Protože je tlak při izobarickém ději konstantní, bude vykonaná práce rovna součinu tlaku a rozdílu objemů.
Pro výpočet celkového tepla, se podíváme, jak to s ním vypadá při obou dějích.
Při izochorickém ději se zvyšuje tlak plynu a podle stavové rovnice i jeho teplota. Protože plyn ani vnější síly nekonají práci, musí se zvyšovat jeho vnitřní energie díky dodávanému teplu. Toto teplo můžeme spočítat pomocí molární tepelné kapacity při stálém objemu. Její hodnotu zjistíme pomocí zadané Poissonovy konstanty a Meyerova vztahu.
Při izobarickém ochlazení klesá teplota plynu, a tedy i jeho vnitřní energie. Zároveň dochází ke stlačování plynu, tj. okolí koná práci. Z toho plyne, že plyn musí odevzdávat do okolí teplo. Při výpočtu ještě uvážíme, že při izobarickém snížení objemu na polovinu, musí klesnout i teplota plynu na polovinu, což plyne ze stavové rovnice.
Výsledné teplo dostaneme jako rozdíl tepla odevzdaného a dodaného.
Nyní ještě zbývá určit změnu vnitřní energie plynu během procesu.
Při izochorickém ději se nekoná práce a podle 1. termodynamického zákona je změna vnitřní energie rovna dodanému, respektive odevzdanému teplu. Výpočet tohoto tepla byl komentován výše. Změnu vnitřní energie při izobarickém ději můžeme spočítat opět pomocí teplotního rozdílu a molární tepelné kapacity při stálém objemu (změna vnitřní energie nezávisí na typu děje, ale pouze na změně teploty).
Zápis
p1 = 100 kPa = 105 Pa původní tlak plynu V1 = 10 l = 10 dm3 = 0,01 m3 původní objem plynu \(\kappa = \frac{5}{3}\) Poissonova konstanta W = ? práce vnějších sil Q = ? celkové teplo ΔU = ? změna vnitřní energie plynu během procesu Řešení – výpočet práce
Nejprve stanovíme práci W vnějších sil během celého procesu. Stačí si uvědomit, že při izochorickém ději se žádná práce nekoná. Díky tomu nám stačí spočítat práci vykonanou při ději izobarickém probíhajícím za stálého tlaku p2
\[p_{2}=4p_{1}.\]Pro práci Wp vykonanou plynem platí vztah (jde o děj za stálého tlaku, a proto se můžeme vyhnout integrování)
\[W_p=p\mathrm{\Delta} V,\]do kterého dosadíme zadané hodnoty tlaku a objemu
\[W_p=p_{2}\left( V_{3}-V_{2}\right)=p_{2}\left(\frac{1}{2} V_{1}- V_{1}\right)=-\frac{1}{2} p_{2}V_{1}.\]Pomocí vztahu mezi p1 a p2 dostaneme výsledný vztah pro celkovou práci.
\[W_p = - 2p_{1}V_{1},\]kde p1 je počáteční tlak a V1 je počáteční objem.
Záporné znaménko znamená, že práci nekoná plyn, ale vnější síly, což odpovídá izobarickému stlačování. Vnější síly tedy vykonají práci
\[W = 2p_{1}V_{1}.\]Řešení – výpočet tepla
Při výpočtu tepla si musíme uvědomit, že při izochorickém zvýšení tlaku na čtyřnásobnou hodnotu se nekoná práce a zároveň dochází ke zvýšení teploty na hodnotu T2 = 4T1 (plyne to z faktu, že pro izochorický děj V = konst. je podle stavové rovnice ideálního plynu podíl \(\frac{p}{T}\) konstantní).
Díky tomu roste vnitřní energie plynu a teplo tedy musí být systému dodáváno. Pro velikost takto dodaného tepla Q1 (a zároveň zvýšení vnitřní energie ΔU1) pak platí:
\[Q_{1} = \mathrm{\Delta} U_{1} = C_{V}n\left( T_{2}-T_{1}\right) = \frac{3}{2} nR\left( 4 T_{1}-T_{1}\right) = \frac{9}{2} nRT_{1}.\]Pro výpočet Q1 ještě využijeme stavovou rovnici ideálního plynu ve tvaru
\[nRT_{1} = p_{1}V_{1},\]a dostáváme
\[Q_{1} = \frac{9}{2} p_{1}V_{1}\]Hodnotu CV lze spočítat ze zadané Poissonovy konstanty pomocí vzorce
\[\kappa = \frac{C_{p}}{C_{V}}\]a Meyerova vztahu \(C_{p} = C_{V} + R.\)
Dosazením získáme:
\[\kappa = \frac{C_{p}}{C_{V}} = \frac{C_{V}+R}{C_{V}} = 1+\frac{R}{C_{V}}\, \Rightarrow\] \[\Rightarrow \, C_{V} = \frac{R}{\kappa - 1} = \frac{R}{\frac{5}{3} - 1} = \frac{3}{2}R\]A pro Cp platí
\[C_{p} = \kappa C_{V} = \frac{5}{3}\, \cdot \, \frac{3}{2}R = \frac{5}{2}R.\]Při izobarickém ochlazování klesá teplota plynu, což znamená, že se snižuje i jeho vnitřní energie, a to o hodnotu ΔU2. Navíc vnější síly vykonají práci W. Díky tomu musí plyn v souladu s 1. termodynamickým zákonem odevzdat do okolí teplo Q2 (teplo Q2 vyjde se záporným znaménkem, protože se jedná o teplo odevzdané soustavou):
\[Q_{2} = C_{p}n\left( T_{3}-T_{2}\right) = \frac{5}{2} Rn\left( \frac{1}{2}T_{2}- T_{2}\right) = -\frac{5}{4} RnT_{2} \] \[Q_{2} = -\frac{5}{4} p_{2}V_{2} = -5 p_{1}V_{1}\]Při výpočtu jsme uvážili fakt, že při izobarickém snížení objemu na polovinu, musí dojít rovněž k ochlazení na polovinu původní termodynamické teploty (to plyne ze skutečnost, že pro stálý tlak platí \(\frac{V}{T} = konst.\)). Následně jsme užili opět stavovou rovnici pro ideální plyn ve tvaru \(nRT_{2} = p_{2}V_{2}\).
Celkové teplo odevzdané plynem během procesu je dáno součtem tepla Q1 dodaného při izochorickém ději a tepla Q2 odevzdaného plynem během izobarického ochlazení.
Bude platit:
\[Q = Q_{1}+Q_{2} =\frac{9}{2} p_{1}V_{1} - 5 p_{1}V_{1}\] \[Q = - \frac{1}{2} p_{1}V_{1}\]Řešení – určení změny vnitřní energie
Mezi stavy 1 a 2 (viz obrázek) roste vnitřní energie plynu. Protože jde o izochorický děj, rovná se změna vnitřní energie dodanému teplu.
\[\mathrm{\Delta} U_{1} = Q_{1} = \frac{9}{2} nRT_{1}.\]Při izobarickém ochlazování (děj mezi stavy 2 a 3) klesá teplota plynu, což znamená, že se snižuje i jeho vnitřní energie. Její změnu označíme ΔU2, a spočítáme následujícím způsobem (záporná hodnota odpovídá poklesu vnitřní energie):
\[\mathrm{\Delta} U_{2} = C_{V}n\left( T_{3}-T_{2}\right) = \frac{3}{2} Rn\left( \frac{1}{2}T_{2}- T_{2}\right) = -\frac{3}{4} RnT_{2} \]Pozn.: Změna vnitřní energie nezávisí na typu děje, který s plynem probíhá, ale závisí u ideálního plynu pouze na změně teploty. Konstantou úměrnosti mezi změnou vnitřní energie a změnou teploty je právě CV. Naopak dodané či odevzdané teplo závisí na typu děje, proto při výpočtu tepla musíme použít vždy tepelnou kapazitu odpovídající danému ději.
Opět jsme využili stavovou rovnici a vztahy platné pro izobarický děj a vztah upravíme.
\[\mathrm{\Delta} U_{2}= -\frac{3}{4} p_{2}V_{2} = -3 p_{1}V_{1}\]Nyní již známe vše potřebné proto, abychom mohli určit požadované hodnoty. Celkový přírůstek vnitřní energie ΔU je dán vzorcem
\[\mathrm{\Delta} U = \mathrm{\Delta} U_{1} + \mathrm{\Delta} U_{2} = \frac{9}{2} p_{1}V_{1} - 3 p_{1}V_{1}.\] \[\mathrm{\Delta} U = \frac{3}{2} p_{1}V_{1}\]Při výpočtu jsme uvážili fakt, že při prvním ději vnitřní energie roste a tedy ji bereme s kladným znaménkem, při druhém klesá a tedy ji bereme se záporným znaménkem.
Kladné znaménko u celkové změny vnitřní energie znamená, že vnitřní energie plynu vzrostla.
Protože vnitřní energie je stavová veličina, a tedy její změna závisí jen na počátečním a koncovém stavu, lze ji vypočítat pouze pomocí rozdílu teplot T3 − T1:
\[\mathrm{\Delta}U = nC_{V}\left( T_{3} - T_{1} \right)\]Pro teplotu T3 platí:
\[T_3 = \frac{1}{2}T_2=\frac{1}{2} 4 T_1 = 2T_1\]a po dosazení dostáváme:
\[\mathrm{\Delta}U = nC_{V}\left( 2T_{1} - T_{1} \right) = nC_{V}T_{} = n \left(\frac{3}{2}R\right) T_1 = \frac{3}{2}p_1V_1, \]tj. stejný výsledek jako předchozím postupem.
Číselné dosazení
\[W = 2 p_{1}V_{1} = 2\cdot{10^{5}}\cdot{0{,}01}\, \mathrm{J} = 2000\, \mathrm{J}\] \[W = 2\, \mathrm{kJ}\] \[Q = - \frac{1}{2} p_{1}V_{1} = - \frac{1}{2}\cdot 10^{5}\cdot 0{,}01\, \mathrm{J} = - 500\, \mathrm{J}\] \[Q = - 0{,}5\, \mathrm{kJ}\] \[\mathrm{\Delta} U = \frac{3}{2} p_{1}V_{1}= \frac{3}{2}\cdot 10^{5}\cdot 0{,}01\, \mathrm{J} = 1500\, \mathrm{J}\] \[\mathrm{\Delta} U = 1{,}5\, \mathrm{kJ}\]Odpověď
Vnější síly vykonaly práci 2 kJ, plyn odevzdal teplo 0,5 kJ a vnitřní energie plynu vzrostla o hodnotu 1,5 kJ.
Komentář
Všimněte si platnosti vztahu ΔU = W + Q. Tento vztah neudává nic jiného než splnění 1. termodynamického zákona pro daný proces. W je kladné, protože to je práce konaná vnějšími silami a teplo Q je záporné, protože plyn během daného děje teplo odevzdal.