Sbírka řešených úloh

Diagramy cyklického děje

Úloha číslo: 341

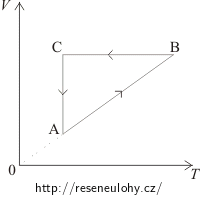
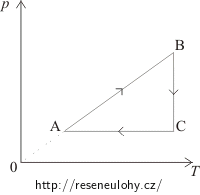
Ideální plyn stálé hmotnosti vykonává kruhové děje ABCA (dle obrázků). Překreslete tyto děje do pV–diagramu.

a)	b)

Určete dále, ve kterých fázích plyn přijímá teplo od okolí a kdy je odevzdává, kdy koná práci plyn a kdy okolí.

• Nápověda – jak překreslit diagramy

  Pro každou část diagramu si nejprve rozmyslete, která ze stavových veličin popisujících plyn (p, V, T) je konstantní a které jsou si sobě úměrné. Potom rozhodněte, jak daný děj zakreslit do pV–diagramu.

• Nápověda – kdy se koná práce a předává teplo

  Jestliže objem plynu

  • roste, potom plyn koná práci (rozpíná se),
  • je konstantní, potom nekoná práci ani plyn, ani okolí,
  • klesá, potom koná práci okolí (plyn je stlačován), tj. uvažujeme „práci plynu zápornou“.

  Vnitřní energie ideálního plynu je úměrná teplotě, tj. pokud se teplota mění, tak se stejným způsobem mění i vnitřní energie.

  Dodané či odevzdané teplo potom již lze určit pomocí zákona zachování energie, kterému se v tomto případě obvykle říká první termodynamický zákon.

• Řešení – překreslení diagramu a)

  Z VT–diagramu vidíme:

  

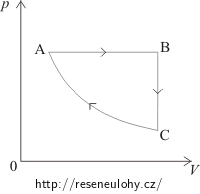
  V části AB je objem plynu úměrný teplotě. To znamená, že v této části je tlak konstantní, jedná se o izobarický děj. Ten je v pV–diagramu znázorněn vodorovnou úsečkou. Protože od A k B roste objem, bude i v pV–diagramu stav A vlevo a stav B vpravo.

  V části BC je konstantní objem, jedná se izochorický děj v pV–diagramu znázorněný svislou úsečkou. Protože od B k C klesá teplota, bude klesat i tlak a stav C bude pod stavem B.

  Při přechodu od stavu C ke stavu A je konstantní teplota = izotermický děj, v pV–diagramu znázorněný částí hyperboly.

• Řešení – energetická bilance a)

  část cyklu	energetická bilance
  AB izobarický děj	zvětšuje se objem ⇒ plyn koná práci roste teplota ⇒ roste vnitřní energie ⇒ musíme dodávat teplo dodané teplo = přírůstek vnitřní energie + práce vykonaná plynem
  BC izochorický děj	nemění se objem ⇒ práce není konána ani plynem ani okolím klesá tlak ⇒ klesá i teplota ⇒ klesá vnitřní energie ⇒ odebíráme teplo odevzdané teplo = úbytek vnitřní energie
  CA izotermický děj	konstantní teplota ⇒ nemění se vnitřní energie klesá objem plynu ⇒ plyn je stlačován ⇒ okolí koná práci aby zůstala konstantní teplota při stlačování, musíme plyn chladit ⇒ plyn odevzdává teplo práce vykonaná okolím = teplo odevzdané plynem

• Řešení – překreslení diagramu b)

  Z pT–diagramu vidíme:

  

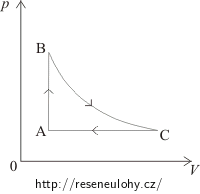
  V části AB je tlak úměrný teplotě, to znamená, že objem zůstává konstantní a jedná se izochorický děj. V pV–diagramu půjde o svislou úsečku. Tlak od A k B roste, proto i v pV–diagramu bude stav A pod stavem B.

  Mezi stavy B a C je konstantní teplota, jedná se o izotermický děj v pV–diagramu zakreslený pomocí hyperboly tak, aby objem rostl.

  Při přechodu od C k A je konstantní tlak = izobarický děj. Do pV–diagramu ho zakreslíme jako vodorovnou úsečku směrem doleva, protože objem klesá.

• Řešení – energetická bilance b)

  část cyklu	energetická bilance
  AB izochorický děj	nemění se objem ⇒ práce není konána ani plynem ani okolím roste tlak ⇒ roste i teplota ⇒ roste vnitřní energie ⇒ dodáváme teplo dodané teplo = přírůstek vnitřní energie
  BC izotermický děj	konstantní teplota ⇒ nemění se vnitřní energie roste objem plynu ⇒ plyn se rozpíná ⇒ plyn koná práci aby zůstala konstantní teplota při rozpínání, musíme plyn ohřívat ⇒ plyn přijímá teplo práce vykonaná plynem = teplo dodané plynu
  CA izobarický děj	zmenšuje se objem plynu ⇒ okolí koná práci (stlačuje plyn) klesá teplota ⇒ klesá vnitřní energie ⇒ musíme odebírat teplo odebrané teplo = úbytek vnitřní energie + práce vykonaná okolím