Kapilára se zataveným koncem
Úloha číslo: 2031
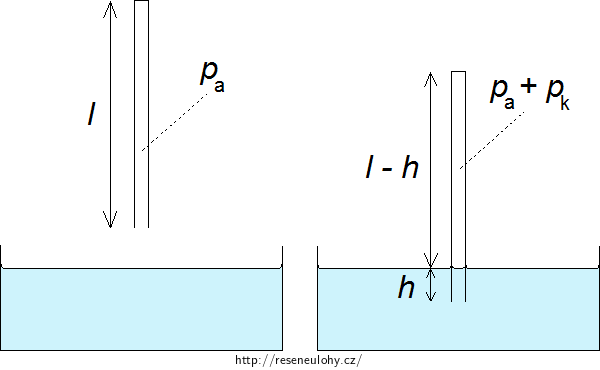
Skleněná kapilára o vnitřním průměru d = 0,2 mm a délce l = 20 cm je na jednom konci zatavena. Druhým koncem je ponořena do vody tak, že její podélná osa je svislá a povrchy vody vně i uvnitř kapiláry jsou ve stejné výši. Přitom je pod vodou část kapiláry o délce h = 2,9 mm. Jak velké je povrchové napětí vody vůči vzduchu?
Zápis
r = 0,1 mm = 10−4 m vnitřní poloměr kapiláry l = 20 cm = 2·10−1 m délka celé kapiláry h = 2,9 mm = 2,9·10−3 m délka ponořené části kapiláry pa = 105 Pa atmosferický tlak σ = ? povrchové napětí vody Rozbor
Nejprve si rozmyslíme, co se stane se vzduchem v kapiláře, když ji ponoříme do vody. Vzduch na začátku vyplňuje celou kapiláru a má atmosférický tlak. Po ponoření kapiláry vnikne dovnitř voda, objem vzduchu se zmenší a jeho tlak vzroste právě o kapilární tlak.
Vzduch můžeme považovat za běžných podmínek za ideální plyn. Při ponořování do vody se navíc nebude měnit teplota vzduchu. Pro vzduch v kapiláře před a po ponoření můžeme napsat stavovou rovnici pro izotermický děj. Z ní pak vyjádříme kapilární tlak. Ten můžeme vyjádřit také pomocí poloměru kapiláry a hledaného povrchového napětí vody.
Nápověda 1 - tlak a objem vzduchu uvnitř kapiláry
Promyslete si, jaký je tlak a objem vzduchu v kapiláře před ponořením a po ponoření kapiláry do vody.
Nápověda 2 - stavová rovnice
Vzduch můžeme považovat za běžných podmínek za ideální plyn. Napište stavovou rovnici pro vzduch v kapiláře před jejím ponořením a po ponoření do vody. Uvědomte si, za jaký děj můžeme stlačení vzduchu při vniknutí vody do kapiláry považovat.
Nápověda 3 - vztah pro výpočet kapilárního tlaku
Připomeňte si vztah pro výpočet kapilárního tlaku. Kapilární tlak si můžeme vyjádřit také ze stavové rovnice. Z rovnosti obou vztahů pak určíme povrchové napětí vody.
Řešení nápovědy 3 - vztah pro výpočet kapilárního tlaku
Pro kapilární tlak pk platí vztah
\[p_\mathrm{k} = \frac{2σ}{r},\tag{6}\]kde σ je povrchové napětí kapaliny a r je poloměr kapiláry.
Celkové řešení
Před ponořením kapiláry do vody je uvnitř kapiláry atmosférický tlak vzduchu pa.
Objem kapiláry V1 vypočítáme jako
\[V_\mathrm{1} = πr^{2}l,\tag{1}\]kde r je poloměr kapiláry a l je délka vnitřní stěny kapiláry.
Součin tlaku a objemu vzduchu v kapiláře je před ponořením
\[p_\mathrm{1}V_\mathrm{1} = p_\mathrm{a}πr^{2}l.\]Po ponoření do vody se v kapiláře zmenší objem vzduchu na V2
\[V_\mathrm{2} = πr^{2}(l−h),\tag{2}\]kde h je výška hladiny vody uvnitř kapiláry.
Zároveň se tlak vzduchu uvnitř zvýší o kapilární tlak vody pk. V kapiláře tak bude tlak p2 o velikosti
\[p_\mathrm{2} = p_\mathrm{a} + p_\mathrm{k}.\tag{3}\]Součin tlaku a objemu vzduchu v kapiláře tak bude po ponoření roven
\[p_\mathrm{2}V_\mathrm{2} = πr^{2}(p_\mathrm{a} + p_\mathrm{k})(l−h).\]Podle stavové rovnice pro izotermický děj platí
\[p_\mathrm{1}V_\mathrm{1} = p_\mathrm{2}V_\mathrm{2}\tag{4}\]po dosazení ze vztahů (1), (2) a (3) do stavové rovnice dostáváme
\[p_\mathrm{a}πr^{2}l = πr^{2}(p_\mathrm{a} + p_\mathrm{k})(l−h).\tag{5}\]Vztah upravíme a vyjádříme z něho kapilární tlak
\[p_\mathrm{k} = \frac{p_\mathrm{a}h}{l−h}\]Chceme zjistit velikost povrchového napětí vody. Známe-li velikost kapilárního tlaku, můžeme z něho dopočítat velikost povrchového napětí σ s využitím vztahu
\[p_\mathrm{k} = \frac{2σ}{r}.\tag{6}\]Dosazením vztahu (6) do upraveného vztahu (5) dostáváme vztah pro výpočet povrchového napětí vody
\[σ = \frac{p_\mathrm{a}rh}{2(l−h)}.\tag{7}\]Číselné dosazení
Velikost povrchového napětí vody vypočítáme ze vztahu (7)
\[σ = \frac{p_\mathrm{a}rh}{2(l−h)}.\]Po dosazení hodnot ze zadání dostaneme rovnici
\[σ = \frac{10^{5}·10^{−4}·2{,}9·10^{−3}}{2·(2·10^{−1}−2{,}9·10^{−3})} N·m^{−1}\] \[σ \dot{=}\, 74·10^{−3} N·m^{−1}.\]Odpověď
Povrchové napětí vody je přibližně 74·10−3 N·m−1.
Poznámka
Povrchové napětí vody závisí na její teplotě. S rostoucí teplotou povrchové napětí klesá. Vypočítali jsme, že voda má povrchové napětí σ = 74·10−3 N·m−1, tomuto povrchovému napětí přibližně odpovídá teplota 11 °C.
Tabulku závislosti povrchového napětí na teplotě jsme našli na webu Converter.