Debyeův-Scherrerův difraktogram
Úloha číslo: 2282
Naměřili jsme Debye-Scherrerův difraktogram pro hliníkový prášek a získali hodnoty Braggových úhlů \(\theta\) uvedené v tabulce. Měření bylo prováděno se zářením \(\mathrm{Cu}\:K\alpha\) o vlnové délce \(1{,}5406\,Å\).
| 19,48° | 41,83° |
| 22,64° | 50,35° |
| 33,00° | 57,05° |
| 39,68° | 59,42° |
Určete mřížový parametr hliníku, ze kterého se prášek skládal.
Debye-Scherrerova metoda
Debyeova-Scherrerova metoda využívá rentgenovou difrakci na velmi jemných prášcích uzavřených ve skleněné kapiláře. V prášku je velmi mnoho krystalků, z nichž každý je orientován určitým způsobem. V celém vzorku jsou potom přibližně stejně zastoupeny všechny možné orientace. Pokud použijeme monochromatické rentgenové záření, budou difraktovat všechny roviny \({hkl}\) splňující Braggovu podmínku
\[2d_{hkl}\sin\theta_{hkl}=n\lambda,\]kde \(d_{hkl}\) je mezirovinná vzdálenost, \(\theta_{hkl}\) je difrakční úhel a \(\lambda\) je vlnová délka použitého záření. Ze vzorku nám tedy budou vycházet kužele difragovaných paprsků s vrcholovým úhlem \(4\theta_{hkl}\).
Situaci pro dvě různé množiny rovin ukazuje obrázek.
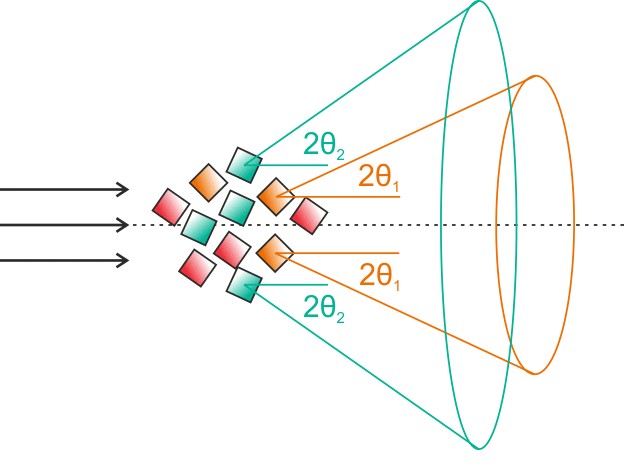
Pro nějakou mezirovinnou vzdálenost \(d_1\) najdeme krystalky vhodně orientované tak, že množina rovin s mezirovinnými vzdálenostmi \(d_1\) v nich bude s přicházejícím zářením svírat úhel \(\theta_1\), pro který bude platit Braggova podmínka \(2d_{1}\sin\theta_{1}=\lambda\). V našem případě jsou to ty oranžové. Tato množina rovin je poté zodpovědná za kužel difragovaného záření s vrcholovým úhlem \(4\theta_{1}\).
Podobně si můžeme vzít jinou mezirovinnou vzdálenosti \(d_2\), ke které najdeme jinak vhodně orientované krystalky, v obrázku zelené. Opět pro množinu rovin s mezirovinnou vzdáleností \(d_2\) v těchto vhodně orientovaných krystalcích bude platit Braggova podmínka ve tvaru \(2d_{2}\sin\theta_{2}=\lambda\), kde \(\theta_{2}\) je úhel mezi přicházejícím zářením a množinou rovin. Ze vzorku bude vycházet další kužel o vrcholovém úhlu \(4\theta_{2}\).
Tyto kužely budou tvořit na detektoru soustředné kružnice. Z jejich polohy určíme Braggovy úhly \(\theta\). Poté můžeme z Braggovy podmínky pro první difrakční řád \(n=1\) zapsat
\[\sin^2 \theta=\frac{\lambda^2}{4 d^2_{hkl}}.\]Pro látky s kubickou mřížkou platí
\[d_{hkl}=\frac{a}{\sqrt{h^2+k^2+l^2}},\]a proto
\[\sin^2 \theta=\frac{(h^2+k^2+l^2)\lambda^2}{4 a^2}.\]Změříme-li Braggovy úhly \(\theta\) příslušející různým množinám rovin \({hkl}\) a odhadneme-li, jakému součtu \(h^2+k^2+l^2\) tyto reflexe přísluší, můžeme mřížový parametr \(a\) určit lineární regresí z předchozího vztahu.
Nápověda: Indexování difrakčního záznamu
Nejprve musíme difrakční záznam oindexovat, to znamená rozhodnout se, kterému Braggovu úhlu \(\theta\) přísluší jaké hodnoty \(h,k,l\) a tudíž i součet \(h^2+k^2+l^2\). To se obvykle dělá metodou „poučený pokus-omyl“.
Nápověda: Určení mřížového parametru regresí
Pokud máme celý difrakční záznam oindexovaný, můžeme přikročit k určení mřížového parametru. To můžeme udělat lineární regresí na základě vztahu
\[\sin^2 \theta=\frac{(h^2+k^2+l^2)\lambda^2}{4 a^2}.\]Celé řešení: Určení mřížového parametru
Difrakční záznam po oindexování vypadá takto:
\(\theta\) \(\sin^2\theta\) \(h\) \(k\) \(l\) \(h^2+k^2+l^2\) \(a\) \(19{,}48°\) \(0{,}11121\) \(1\) \(0\) \(0\) \(1\) \(2{,}3099\) \(22{,}64°\) \(0{,}14818\) \(1\) \(1\) \(0\) \(2\) \(2{,}8300\) \(33{,}00°\) \(0{,}29663\) \(1\) \(1\) \(1\) \(3\) \(2{,}4497\) \(39{,}68°\) \(0{,}40768\) \(2\) \(0\) \(0\) \(4\) \(2{,}4128\) \(41{,}83°\) \(0{,}44479\) \(2\) \(1\) \(0\) \(5\) \(2{,}5827\) \(50{,}35°\) \(0{,}59283\) \(2\) \(1\) \(1\) \(6\) \(2{,}4506\) \(57{,}05°\) \(0{,}7042\) \(2\) \(2\) \(0\) \(8\) \(2{,}5964\) \(59{,}42°\) \(0{,}74118\) \(2\) \(2\) \(1\) \(9\) \(2{,}6842\) Použitím lineární regrese dospějeme k hodnotě mřížového parametru
\[a=2{,}673\,Å.\]


