Sbírka řešených úloh

Účinnost Dieselova cyklu

Úloha číslo: 411

• Nápověda

  Nakreslete si cyklus do p-V diagramu.

  Rozmyslete si, jak je v p-V diagramu cyklického děje znázorněna práce, kterou plyn vykoná během jednoho cyklu, a při kterých dějích Dieselova cyklu je plynu dodáváno teplo.

• Rozbor

  Abychom mohli vyjádřit účinnost Dieselova cyklu, musíme znát práci vykonanou plynem během jednoho oběhu a teplo, které plyn během jednoho cyklu přijal. Účinnost je pak podíl práce a dodaného tepla.

  Celková práce vykonaná plynem je v p–V diagramu udána jako obsah plochy ohraničené cyklem. Tuto práci spočítáme sečtením práce vykonané plynem při izobarické expanzi a adiabatické expanzi. Pak ještě musíme odečíst práci vykonanou okolím při adiabatické kompresi. Při izochorickém ochlazení se žádná práce nekoná.

  Dále spočítáme dodané teplo. Při adiabatických změnách nedochází k tepelným výměnám, tedy je při nich dodané teplo nulové. Při izochorickém ději je teplo plynu odebíráno. Takže jediným dějem, při kterém dodáváme plynu teplo, je izobarická expanze. Hledané teplo vyjádříme pomocí molární tepelné kapacity při stálém tlaku. Samotnou molární tepelnou kapacitu vyjádříme z definice Poissonovy konstanty a Meyerova vztahu.

  Nakonec oba výsledky dosadíme do vztahu pro účinnost a upravíme pomocí definic kompresního a plnícího poměru.

• Řešení

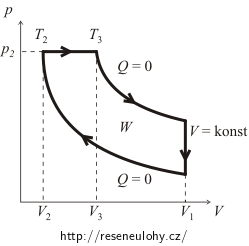
  Předně si musíme uvědomit, jak vůbec Dieselův cyklus vypadá v p–V diagramu. Základní představu (získanou ze stavové rovnice ideálního plynu pV/T = konst. a z Poissonova zákona pro adiabatický děj pV^κ = konst., kde p je tlak plynu, V jeho objem, T teplota a κ je Poissonova konstanta) je uvedena na následujícím obrázku.

  

  Víme, že účinnost cyklu η je dána vztahem

  \[\eta = \frac{W}{Q_{dod}},\]

  kde W je práce vykonaná plynem za jeden cyklus (je dána rozdílem práce plynu W_pl a práce vnějších sil W_ok, v diagramu je znázorněna jako obsah plochy ohraničené cyklem) a Q_dod teplo, které plyn během jednoho cyklu přijal.

   

  Vykonaná práce

  Je potřeba zjistit, kdy vlastně plyn koná práci. Určitě to nebude při izochorickém ochlazení (nemění se objem) ani při adiabatické kompresi (tehdy konají práci W_ok vnější síly). Při izobarické expanzi vykoná plyn práci W_pl1 a při adiabatické expanzi pak práci W_pl2.

  Práci W_pl1 stačí spočítat jako součin tlaku a rozdílu konečného a počátečního objemu, protože děj probíhá za stálého tlaku.

  \[W_{pl1} = p_{2}\mathrm{\Delta} V = p_{2}\left( V_{3}-V_{2} \right) = p_{2}\left( \varphi V_{2}-V_{2} \right) =\] \[= p_{2}V_{2}\left( \varphi - 1\right) = nRT_{2}\left( \varphi - 1\right).\]

   

  Práci W_pl2 budeme muset spočítat pomocí integrálního počtu, protože při adiabatickém ději se mění tlak. Pro vyjádření tlaku použijeme Poissonův zákon:

  \[pV^{\kappa}=p_{2}V_{3}^{\kappa}\] \[p=p_{2}\frac{V_{3}^{\kappa}}{V^{\kappa}},\]

  kde p₂, V₃ určují počáteční stav zkoumaného děje. Plyn se pak rozepne na objem V₁. Počáteční a koncový objem použijeme jako meze integrálu pro výpočet práce.

  \[W_{pl2} = \int_{V_{3}}^{V_{1}}p\, \mathrm{d}V = \int_{V_{3}}^{V_{1}}p_{2}\frac{V_{3}^{\kappa}}{V^{\kappa}}\, \mathrm{d}V = p_{2}V_{3}^{\kappa}\int_{V_{3}}^{V_{1}}V^{-\kappa}\, \mathrm{d}V = \] \[= p_{2}V_{3}^{\kappa}\left[ \frac{V^{-\kappa + 1}}{-\kappa + 1} \right]_{V_{3}}^{V_{1}}\, = p_{2}V_{3}^{\kappa}\frac{(V_{1})^{1-\kappa} - (V_{3})^{1-\kappa}}{1-\kappa} \] \[= p_{2}V_{3}\frac{\left( \frac{V_{3}}{V_{1}}\right) ^{\kappa - 1} - 1}{1 - \kappa}\]

  Nyní do získaného vztahu dosadíme kompresní a plnící poměr za objemy V₁ a V₃:

  \[V_{1} = \varepsilon V_{2}\] \[V_{3}=\varphi V_{2}\]

  Dosazením dostaneme rovnici:

  \[W_{pl2} = p_{2}V_{2}\varphi\frac{\left( \frac{\varphi V_{2}}{\varepsilon V_{2}}\right) ^{\kappa - 1} - 1}{1 - \kappa} = p_{2}V_{2}\frac{\varphi ^{\kappa}\,\varepsilon^{1-\kappa} - \varphi}{1-\kappa}\]

  Objemu V₂ v posledním vztahu se „zbavíme“ díky stavové rovnici pro ideální plyn p₂V₂ = nRT₂. Tím dostaneme konečný vztah pro práci W_pl2:

  \[W_{pl2} = nRT_{2}\frac{\varphi ^{\kappa}\,\varepsilon^{1-\kappa} - \varphi}{1-\kappa}\]

   

  Nyní musíme podobným způsobem spočítat práci okolních sil vykonanou při adiabatické kompresi. Pro vyjádření tlaku opět použijeme Poissonův zákon, vyjdeme však z konečného stavu zkoumané části cyklu popsané tlakem p₂ a objemem V₃. Před kompresí měl plyn objem V₁.

  \[pV^{\kappa}=p_{2}V_{2}^{\kappa}\] \[p=p_{2}\frac{V_{2}^{\kappa}}{V^{\kappa}},\]

  Získaný tlak opět dosadíme do integrálu pro výpočet práce.

  \[W_{ok} = \int_{V_{1}}^{V_{2}}p\, \mathrm{d}V = \int_{V_{1}}^{V_{2}}p_{2}\frac{V_{2}^{\kappa}}{V^{\kappa}}\, \mathrm{d}V = p_{2}V_{2}^{\kappa}\int_{V_{1}}^{V_{2}}V^{-\kappa}\, \mathrm{d}V = \] \[= p_{2}V_{2}^{\kappa}\left[ \frac{V^{-\kappa + 1}}{-\kappa + 1} \right]_{V_{1}}^{V_{2}}\, = p_{2}V_{2}^{\kappa}\frac{(V_{2})^{1-\kappa} - (V_{1})^{1-\kappa}}{1-\kappa} \] \[= p_{2}V_{2}\frac{1 - \left( \frac{V_{2}}{V_{1}}\right) ^{\kappa - 1}}{1 - \kappa}\]

  Nyní do získaného vztahu dosadíme kompresní poměr:

  \[\varepsilon = \frac{V_{1}}{V_{2}}\]

  Dosazením dostaneme rovnici:

  \[W_{ok} = p_{2}V_{2}\frac{1 - \,\varepsilon ^{1 - \kappa}}{1 - \kappa}\]

  Objemu V₂ v posledním vztahu se „zbavíme“ díky stavové rovnici pro ideální plyn p₂V₂ = nRT₂. Tím dostaneme konečný vztah pro práci W_ok:

  \[W_{ok} = nRT_{2}\frac{1 - \,\varepsilon ^{1 - \kappa}}{1 - \kappa}\]

   

  Pro celkovou vykonanou práci W potom můžeme psát

  \[W = W_{pl1} + W_{pl2} - W_{ok} = \] \[nRT_{2}\left( \varphi - 1\right) + nRT_{2}\left( \frac{\varphi ^{\kappa}\varepsilon ^{1-\kappa} - \varphi}{ \left( 1 - \kappa \right) }\right) - nRT_{2}\left( \frac{\varepsilon ^{-\kappa +1}- 1}{ \left( 1 - \kappa \right) }\right) =\] \[= nRT_{2}\left( \varphi - 1 + \frac {\varphi ^{\kappa}\varepsilon ^{1-\kappa} - \varphi - \varepsilon ^{-\kappa +1}+1}{1-\kappa}\right) .\]

  V tuto chvíli je samozřejmě možné namítnout, že uvedený výsledek nám není nic platný, protože obsahuje dvě proměnné, které neznáme (látkové množství n, teplotu T₂). Brzy však uvidíme, že se tyto proměnné v dalším výpočtu zkrátí.

   

  Dodané teplo

  Přistupme proto k určení tepla Q_dod dodaného do systému. Je třeba si uvědomit, že při adiabatických změnách k žádným tepelným výměnám nedochází, a proto je při nich teplo dodané plynu rovno nule. Při izochorickém ochlazení je teplo ze systému naopak odebíráno, což vede při nulové vykonané práci ke snížení vnitřní energie. Jediným dějem, kdy je tedy teplo plynu během cyklu dodáváno, je tedy izobarická expanze. Tehdy je plynu dodáno teplo

  \[Q_{dod} = nC_{p}\left( T_{3}-T_{2}\right),\]

  přičemž část tohoto tepla se zužitkuje jako práce vykonaná plynem, zbytek poslouží ke zvýšení vnitřní energie. Využitím známého vztahu pro izobarický děj

  \[\frac{V}{T} = konst\]

  pak dostáváme:

  \[Q_{dod} = nC_{p}\left( T_{3}-T_{2}\right) = nC_{p}\left( \varphi T_{2}-T_{2}\right) = nC_{p}T_{2}\left( \varphi - 1\right).\]

  Nyní je třeba stanovit molární tepelnou kapacitu plynu C_p. Užitím definičního vztahu pro Poissonovu konstantu

  \[\kappa = \frac{C_{p}}{C_{V}}\]

  a Meyerova vztahu

  \[C_{p} = C_{V} + R\]

  postupně dostáváme:

  \[\kappa = \frac{C_{p}}{C_{V}} = \frac{C_{V} + R}{C_{V}} = 1+\frac{R}{C_{V}}\Rightarrow \frac{R}{C_{V}} = \kappa -1 \Rightarrow C_{V} = \frac{R}{\kappa - 1}\] \[C_{p} = \frac{R}{\kappa - 1} + R = R\left( 1+\frac{1}{\kappa -1}\right).\]

   

  Účinnost

  Nyní konečně dosadíme do vzorce pro účinnost cyklu. Bude platit:

  \[\eta = \frac{W}{Q_{dod}} = \frac {nRT_{2}\left( \varphi - 1 + \frac {\varphi ^{\kappa}\varepsilon ^{1-\kappa} - \varphi - \varepsilon ^{-\kappa +1}+1}{1-\kappa}\right)}{nC_{p}T_{2}\left( \varphi - 1\right)} = \] \[= \frac{nRT_{2}\left( \varphi - 1 + \frac {\varphi ^{\kappa}\varepsilon ^{1-\kappa} - \varphi - \varepsilon ^{-\kappa +1}+1}{1-\kappa}\right)}{nR\left( 1+\frac{1}{\kappa -1}\right)T_{2}\left( \varphi - 1\right)} \]

  Zkrátíme, rozdělíme na dva zlomky a upravíme složené zlomky:

  \[\eta =\frac{\varphi -1}{\kappa \frac{\varphi -1}{\kappa -1}} +\frac{\frac {\varphi ^{\kappa}\varepsilon ^{1-\kappa} - \varphi - \varepsilon ^{-\kappa +1}+1}{1-\kappa}}{\kappa \frac{\varphi -1}{\kappa -1}} = 1-\frac{1}{\kappa}-\frac{\varphi ^{\kappa}\varepsilon ^{1-\kappa} - \varphi - \varepsilon ^{-\kappa +1}+1}{\kappa \left( \varphi -1\right)} = \] \[=1-\frac{1}{\kappa}-\frac{\varepsilon ^{1-\kappa}\left( \varphi ^{\kappa}-1\right) -\left( \varphi -1\right)}{\kappa \left( \varphi -1\right)} = 1-\frac{1}{\kappa}-\frac{\varepsilon ^{1-\kappa}\left( \varphi ^{\kappa}-1\right)}{\kappa \left( \varphi -1\right)}+ \frac{1}{\kappa}\]

  Pro účinnost tedy dostáváme vztah:

  \[\eta = 1 - \frac{\varepsilon ^{1-\kappa}\left( \varphi ^{\kappa}-1\right)}{\kappa \left( \varphi -1\right)}\]

• Odpověď

  Účinnost Dieselova cyklu je skutečně dána pouze oběma zadanými poměry a Poissonovou konstantou plynu.

  Příslušná funkce má tvar

  \[\eta = 1 - \frac{\varepsilon ^{1-\kappa}\left( \varphi ^{\kappa}-1\right)}{\kappa \left( \varphi -1\right)}.\]