Hustota železa
Úloha číslo: 2274
Železo (Ar = 55,85) při normální teplotě krystalizuje v kubické prostorově centrované mřížce s mřížkovou konstantou 2,87 Å. Při zahřátí na teplotu vyšší než 910 °C (při normálním tlaku) přechází ale v kubickou plošně centrovanou mřížku o mřížkové konstantě rovné 3,55 Å. Má železo v obou modifikacích stejnou hustotu? Určete ji.
Zápis
\[A_r=55{,}85\] \[a_{1}=2{,}87\,\mathrm{Å}=2{,}87{\cdot} 10^{-10}\,\mathrm{m}\] \[a_{2}=3{,}55\,\mathrm{Å}=3{,}55{\cdot} 10^{-10}\,\mathrm{m}\] \[m_{u}=1{,}661{\cdot} 10^{-27}\,\mathrm{kg}\] \[\rho_{1}=?\] \[\rho_{2}=?\]Rozbor
Hustota vyjadřuje hmotnost jednotkového objemu. Určíme ji jako podíl hmotnosti atomů v elementární buňce a jejího objemu. Známe mřížkovou konstantu, takže objem určíme snadno. Při určování hmotnosti atomů v elementární buňce musíme dát pozor na to, že sousední buňky se o některé atomy dělí, a nesmíme je tedy započítat vícekrát.Nápověda 1: Tvary mřížek
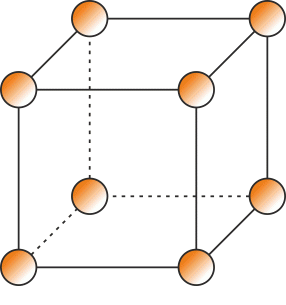
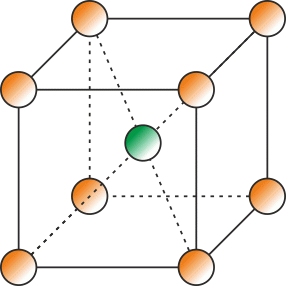
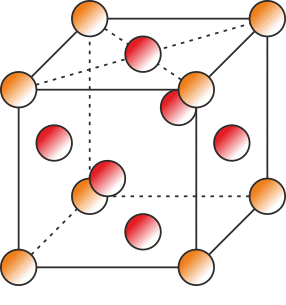
Nejprve si načrtněte, jak vypadá kubická prostorově centrovaná a kubická plošně centrovaná mřížka a jak jsou v nich uspořádány jednotlivé atomy.
Nápověda 2: Výpočet hustoty
Dále zapište vztah pro výpočet hustoty pomocí zadaných veličin: mřížkové konstanty, relativní atomové hmotnosti železa a atomové hmotnostní konstanty. Uvědomte si ale, že v pevné látce je mnoho elementárních buněk naskládáno vedle sebe a na sebe, a tak jsou některé atomy (ty v hranách a stěnách elementární buňky) součástí více přilehlých elementárních buněk. Pokud je nějaký atom součástí dvou sousedních buněk, musíme ho započítat jenom půlkrát, protože jen jeho polovina připadá na jednu z nich. Podobně atom nacházející se v šesti buňkách započítáme jen \(\frac{1}{6}\) krát, a tak dále. Vidíme tedy, že do vzorce pro hustotu je třeba včlenit veličinu n vyjadřující počet atomů připadajících na jednu elementární buňku.
Nápověda 3: Počet atomů na jednu buňku
Vypočtěte počet atomů připadajících na jednu elementární buňku pro oba typy buněk. U každého z atomů si promyslete, jestli je součástí dalších přilehlých elementárních buněk, a pokud ano, tak kolika. Atom poté započtěte odpovídajícím způsobem.
Celkové řešení
Hustotu vypočteme jako
\[\rho = \frac{m}{V},\]kde \(m\) je hmotnost atomů připadajících na jednu elementární buňku a \(V\) je objem elementární buňky. Hmotnost atomů připadajících na jednu buňku vypočteme jako \[m=nm_a,\] kde \(n\) je počet atomů připadajících na jednu buňku a \(m_a\) je hmotnost jednoho atomu železa. Objem kubické elementární buňky je \[V=a^3,\] kde \(a\) je mřížková konstanta. Po dosazení dostáváme
\[\rho = \frac{n m_a}{a^3}.\] Využitím vztahu pro hmotnost atomu \[m_a=A_rm_u,\] kde \(A_r\) je relativní atomová hmotnost železa a \(m_u\) atomová hmotnostní konstanta, získáme konečně \[\rho = \frac{n A_r m_u}{a^3}.\]Pro kubickou prostorově centrovanou mřížku je \(n=2\), a proto
\[\rho_{1} = \frac{2 A_r m_u}{a_{1}^3}.\]Pro kubickou plošně centrovanou mřížku je \(n=4\), a proto
\[\rho_{2} = \frac{4 A_r m_u}{a_{2}^3}.\]Číselný výpočet
\[\rho_{1}=\frac{2 A_r m_u}{a_{1}^3}=\frac{2 {\cdot} 55{,}85 {\cdot} 1{,}661{\cdot} 10^{-27}}{\left( 2{,}87{\cdot} 10^{-10} \right)^3}\,\mathrm{kg\cdot m^{-3}}=7850\,\mathrm{kg\cdot m^{-3}}\] \[\rho_{2}=\frac{4 A_r m_u}{a_{2}^3}=\frac{2 {\cdot} 55{,}85 {\cdot} 1{,}661{\cdot} 10^{-27}}{\left( 3{,}55{\cdot} 10^{-10} \right)^3}\,\mathrm{kg\cdot m^{-3}}=8290\,\mathrm{kg\cdot m^{-3}}\]Odpověď
Hustota železa se v obou modifikacích liší, v případě prostorově centrované mřížky činí
\[\rho_{1}=7850\,\mathrm{kg\cdot m^{-3}}\]a v případě plošně centrované mřížky
\[\rho_{2}=8290\,\mathrm{kg\cdot m^{-3}}.\]Poznámka ke správné terminologii
Krystalovou mřížkou rozumíme množinu bodů (je to geometrický model struktury). Těmto mřížkovým (resp. uzlovým) bodům přiřazujeme atomy, nebo skupiny atomů (tzv. báze) a potom mluvíme o struktuře. Tedy: krystalová mřížka + báze = struktura.
Na úrovni střední školy se často pojem mřížka užívá ve smyslu struktury.