Účinnost skutečného kruhového děje
Úloha číslo: 406
Určete účinnost skutečného kruhového děje skládajícího se z izotermické expanze při teplotě 700 K, izochorického ochlazení, izotermické komprese při teplotě 400 K a následného izochorického ohřátí na počáteční teplotu 700 K. Při izotermické kompresi se plyn stlačil na polovinu svého předchozího objemu.
Měrná tepelná kapacita pracovního plynu při stálém objemu je CV = 6,5R, látkové množství tohoto plynu je 1 mol.
Celý cyklus znázorněte graficky a spočtenou skutečnou účinnost srovnejte s účinností, kterou by měl při práci mezi danými teplotami ideální Carnotův cyklus.
Nápověda
Rozmyslete si, jak je v p–V diagramu znázorněna práce vykonaná plynem. Dále si uvědomte, jak je definovaná účinnost kruhového děje a při kterých dějích plyn přijímá teplo a při kterých ho odevzdává.
Rozbor
Účinnost kruhového děje je podíl práce vykonané plynem během jednoho cyklu a tepla, které bylo plynu během jednoho cyklu dodáno.
Velikost práce vykonané plynem je v p–V diagramu totožná s plochou ohraničenou grafem kruhového děje. Tuto práci můžeme tedy spočítat jako rozdíl práce vykonané plynem při izotermické expanzi a práce vykonané okolím při izotermické kompresi (pro výpočet musíme použít integrální počet, protože tlak je funkcí objemu). Při izochorických dějích se práce nekoná, protože je při nich nulová změna objemu.
Dále si uvědomíme, ve kterých fázích plyn odevzdává teplo a kdy ho přijímá. Plyn odevzdává teplo při izochorickém ochlazení a izotermické kompresi. Plynu teplo dodáváme při izochorickém ohřátí a při izotermické expanzi. První z těchto dvou tepel spočítáme pomocí molární tepelné kapacity a druhé se rovná práci vykonané plynem při jeho expanzi. Nyní již stačí obě tepla sečíst a spolu s celkovou prací vykonanou plynem dosadit do vztahu pro účinnost.
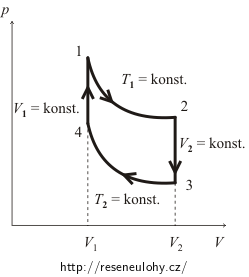
Znázornění děje do p–V diagramu
Především musíme získat představu o tom, jak vypadá celý cyklus v p–V diagramu.
Oba izochorické děje jsou charakterizovány tím, že V = konst, což znamená, že v diagramu jim odpovídají úsečky rovnoběžné se svislou osou. Pro izotermické děje je pak konstantní teplota, což s využitím stavové rovnice ideálního plynu pV = nRT zaručuje konstantnost součinu pV (látkové množství ani univerzální plynová konstanta se pochopitelně během cyklu nemění!). Proto je izoterma v p–V diagramu částí rovnoosé hyperboly.
Celkový průběh cyklu včetně stavů v jednotlivých bodech je patrný z obrázku.
Zápis
T1 = 700 K teplota plynu při izotermické expanzi T2 = 400 K teplota plynu při izotermické kompresi CV = 6,5R měrná tepelná kapacita plynu při stálém objemu n = 1 mol látkové množství plynu V2 = 2V1 plyn byl stlačen na polovinu původního objemu η = ? účinnost tohoto cyklu ηid = ? ideální účinnost Carnotova cyklu pracujícího mezi danými teplotami Řešení
Nyní si uvědomíme, že účinnost cyklu je definována jako podíl práce vykonané plynem za jeden oběh (tj. rozdíl práce vykonané plynem Wpl a práce vykonané okolím Wok, tedy W = Wpl − Wok; v diagramu je výsledek udán jako obsah plochy ohraničené cyklem) a tepla Qdod, které bylo plynu během oběhu dodáno.
Pro požadovanou účinnost tedy platí
\[\eta = \frac{W}{Q_{dod}}.\]Vykonaná práce
Při izochorickém ději se žádná práce nekoná (platí totiž dW = pdV a dV = 0).
U izotermické komprese pak koná práci okolí (když stlačujeme plyn, je to námaha pro nás, ne pro ten plyn). Z toho plyne, že jediný děj, kdy koná práci plyn Wpl, je izotermická expanze (při ní zvětšuje plyn svůj objem, to ho stojí určitou námahu).
Můžeme proto psát:
\[\mathrm{d}W=p\mathrm{d}V\] \[W_{pl}=\int_{V_{1}}^{V_{2}}{p}\, \mathrm{d}V = \int_{V_{1}}^{V_{2}}{\frac{p_{1}V_{1}}{V}}\, \mathrm{d}V = p_{1}V_{1}\ln\frac{V_{2}}{V_{1}} = nRT_{1}\ln\frac{2V_{1}}{V_{1}}\]Pro práci plynu tedy dostáváme:
\[W_{pl}=nRT_{1}\ln2\]Při výpočtu jsme využili vztah pV = p1V1 platící pro izotermický děj (expanze probíhala za stálé teploty T1), výsledek upravili pomocí stavové rovnice a vztahu mezi počátečním a koncovým objemem V2 = 2V1.
Analogicky spočítáme práci vykonanou vnějšími silami při izotermické kompresi. Opět jde o izotermický děj tentokrát však při teplotě T2), a tak bude platit:
\[\mathrm{d}W=p\mathrm{d}V\] \[W_{ok}=-\int_{V_{2}}^{V_{1}}{p}\, \mathrm{d}V = -\int_{V_{2}}^{V_{1}}{\frac{p_{2}V_{2}}{V}}\, \mathrm{d}V = -p_{2}V_{2}\ln\frac{V_{1}}{V_{2}} = \] \[= p_{2}V_{2}\ln\frac{V_{2}}{V_{1}} = nRT_{2}\ln\frac{2V_{1}}{V_{1}}\]Pro práci okolí tedy dostáváme:
\[W_{ok}=nRT_{2}\ln2\]Celková práce vykonaná plynem za jeden cyklus je pak dána vztahem:
\[W=W_{pl}-W_{ok}=nRT_{1}\ln2 - nRT_{2}\ln2\] \[W=nR \left( T_{1}-T_{2}\right)\,\ln2\]Dodané teplo
Nyní je třeba spočítat teplo, které plyn během cyklu přijal. Při izochorickém ochlazení a izotermické kompresi plyn teplo odevzdává (v prvním případě to jde na úkor jeho vnitřní energie, v druhém případě koná okolí práci, vnitřní energie plynu se však díky konstantnosti teploty nezvyšuje, což znamená, že se veškerá práce musí projevit jako teplo předané plynem do okolí).
Teplo Q1dod je dodáno při izochorickém ohřátí (rovná se změně vnitřní energie plynu) a při izotermické expanzi je dodáno teplo Q2dod (to není nic jiného než práce, kterou plyn vykoná při expanzi; jeho vnitřní energie se nemění). Nyní musíme obě dodaná tepla spočítat.
V prvním případě nám pomůže znalost molární tepelné kapacity při stálém objemu CV = 6,5R (jde o izochorický děj).
Proto bude platit:
\[Q_{1dod} = nC_{V}\left( T_{1} - T_{2}\right) = 6{,}5\, \cdot \, Rn\left( T_{1} - T_{2}\right)\]U izotermické expanze si stačí uvědomit, že jsme dodané teplo vlastně již spočítali! Je totiž rovno práci, kterou plyn vykonal při expanzi.
Platí tedy:
\[Q_{2dod} = W_{pl} = nRT_{1}\ln2\]Pro celkové dodané teplo tedy platí:
\[Q_{dod} = Q_{1dod}+Q_{2dod} = 6{,}5Rn\left( T_{1} - T_{2}\right) + nRT_{1}\,\ln2\]Účinnost
Dosazením do vzorce pro účinnost a jednoduchou úpravou pak získáváme konečný výsledek:
\[\eta = \frac{W}{Q_{dod}} = \frac{nR\ln2 \left( T_{1} - T_{2}\right)}{Rn\left( T_{1} - T_{2}\right) + nRT_{1}\ln2} = \frac{\left( T_{1} - T_{2}\right)\ln2}{6{,}5\left( T_{1} - T_{2}\right) + T_{1}\ln2}\]Nyní ještě určíme účinnost ideálního Carnotova cyklu pracujícího mezi stejnými teplotami. Pro něj platí známý vzorec:
\[\eta _{id}= \frac{T_{1}-T_{2}}{T_{1}}\]Číselné dosazení
Účinnost zadaného cyklu:
\[\eta = \frac{\left( T_{1} - T_{2}\right)\,\ln2}{6{,}5 \left( T_{1} - T_{2}\right) + T_{1}\,\ln2} = \frac{\left( 700 - 400\right)\cdot \ln2}{6{,}5\cdot \left( 700 - 400\right) + 700\cdot \ln2}\] \[\eta = 0{,}085\]Účinnost Carnotova cyklu:
\[\eta _{id}= \frac{T_{1}-T_{2}}{T_{1}} = \frac{700-400}{700}\] \[\eta _{id}=0{,}43\]Ve shodě s teorií nám vyšlo, že Carnotův cyklus má pro danou teplotu chladiče a ohřívače vyšší účinnost než má děj uvedený v této úloze.
Odpověď
Účinnost daného cyklu je 8,5 %, zatímco Carnotův cyklus pracující mezi stejnými teplotami by dosáhl účinnosti 43 %.