Sbírka řešených úloh

Kosinova věta

Úloha číslo: 1440

Dokažte následující větu.

Kosinova věta

Nechť \(V\) je reálný vektorový prostor se skalárním součinem \(f\).

Pro každé dva vektory \(x,y\in V\), jejichž úhel je \(\varphi\) platí

\[ \lVert x-y \rVert^2 = \lVert x \rVert^2 + \lVert y \rVert^2 - 2\lVert x \rVert \lVert y \rVert \cos \varphi.\]

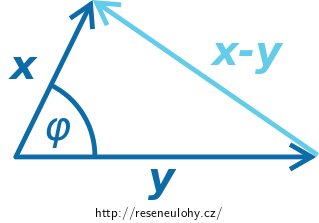
• Strategie

  Normu na levé straně rozepište dle definice normy. Užijte linearity a symetrie skalárního součinu.

  Vzniklý skalární součin vektorů vyjádřete pomocí vztahu pro úhel vektorů.

• Důkaz

  Normu na levé straně rovnosti rozepíšeme dle definice \[ \lVert x-y \rVert^2 = f(x-y,x-y).\] Užijeme linearity \[ \lVert x-y \rVert^2 = f(x,x) - f(y,x) - f(x,y) + f(y,y)\] a symetrie skalárního součinu \(f\) \[ \lVert x-y \rVert^2 = f(x,x) - 2f(x,y) + f(y,y).\] „Identifikujeme“ druhé mocniny norem vektorů \(x,y\) \[ \lVert x-y \rVert^2 = \lVert x \rVert^2 - 2f(x,y) + \lVert y \rVert^2.\] Za skalární součin \(f(x,y)\) dosadíme z definičního vztahu (ii) úhlu vektorů \[ \lVert x-y \rVert^2 = \lVert x \rVert^2 - 2\lVert x \rVert \lVert y \rVert \cos\varphi + \lVert y \rVert^2.\] A v obvyklé formě dostáváme \[ \lVert x-y \rVert^2 = \lVert x \rVert^2 + \, \lVert y \rVert^2 - 2\lVert x \rVert \lVert y \rVert \cos\varphi .\] \[\square\]