Tato úloha neprošla kontrolou správnosti.
Trojúhelníková nerovnost
Úloha číslo: 1438
Má-li se průměrný člověk dostat z bodu \(\mathrm{A}\) do bodu \(\mathrm{B}\), nepoužije k tomu šedý chodník daný vektory \(x,y\), ale zvolí cestu po trávníku, kde je již od pravěku vyšlapaná cesta daná vektorem \(x+y\).
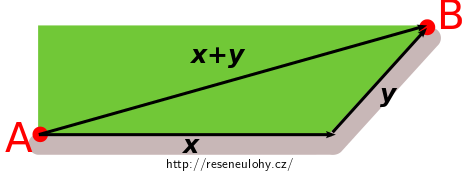Člověk si může být jistý, že si takto cestu nikdy neprodlouží. Dokažte.
Při důkazu věty se bude hodit Cauchy-Schwarzova nerovnost.
Strategie
Vezměte druhou mocninu normy na levé straně nerovnosti a přepište ji dle definice pomocí skalárního součinu. Výraz zjednodušte díky linearitě a symetrii skalárního součinu. Dále užijte nerovnosti \[\forall a\in\mathbb{R}: \qquad a \le |a|\] a následně platnost Cauchy-Schwarzovy nerovnosti.Důkaz
Rozepišme dle definice normy druhou mocninu levé strany nerovnosti. \[\lVert x+y \rVert^2 = f(x+y,x+y) \] Užitím linearity \[\lVert x+y \rVert^2 = f(x,x) + f(y,x) + f(x,y)+ f(y,y) \] a symetrie skalárního součinu dostáváme \[\lVert x+y \rVert^2 = f(x,x) + 2f(x,y)+ f(y,y). \] Ve vzniklém výrazu „identifikujeme“ druhé mocniny norem vektorů \(x,y\). \[\lVert x+y \rVert^2 = \lVert x \rVert^2 + 2f(x,y)+ \lVert y \rVert^2. \] Přidáním absolutní hodnoty získáme nerovnost \[\lVert x+y \rVert^2 \le \lVert x \rVert^2 + 2|f(x,y)|+ \lVert y \rVert^2.\] Užijeme Cauchy-Schwarzovu nerovnost \[\lVert x+y \rVert^2\ \le\ \lVert x \rVert^2 + 2\color{blue}{|f(x,y)|}+ \lVert y \rVert^2\ \color{blue}{\le}\ \lVert x \rVert^2 + 2\color{blue}{\lVert x \rVert\lVert y \rVert}+ \lVert y \rVert^2.\] Vypuštěním střední části nerovnosti máme \[\lVert x+y \rVert^2\ \le\ \lVert x \rVert^2 + 2\lVert x \rVert\lVert y \rVert+ \lVert y \rVert^2.\] Upravíme pravou stranu nerovnosti \[\lVert x+y \rVert^2\ \le\ \big[\lVert x \rVert + \lVert y \rVert\big]^2.\] Odmocněním získáme \[\bigg|\lVert x+y \rVert\bigg|\ \le\ \bigg| \lVert x \rVert + \lVert y \rVert \bigg|.\] Absolutní hodnoty jsou samozřejmě nadbytečné, norma je vždy nezáporná. Tedy \[\lVert x+y \rVert\ \le\ \lVert x \rVert + \lVert y \rVert.\] \[\square\]
