Ověření relace neurčitosti pro základní stav částice v nekonečně hluboké pravoúhlé potenciálové jámě
Úloha číslo: 738
Jednorozměrná nekonečně hluboká pravoúhlá potenciálová jáma je charakterizována potenciální energií
kde L je šířka jámy. Mimo tuto jámu nabývá potenciální energie nekonečné hodnoty V → ∞. Vlnová funkce je rovna nule mimo uvedenou oblast a na hranicích této oblasti. Stav částice nacházející se v této jámě je v čase t = 0 popsán vlnovou funkcí (částice se nachází v základním stavu)
\[\psi(x,0)= \sqrt{{2 \over L}}\, \sin {\,\pi x \over L}\,.\]Spočtěte střední hodnoty a neurčitosti polohy a hybnosti této částice a ověřte, že splňují Heisenbergovu relaci neurčitosti
\[\Delta x \,\Delta p \geq {\hbar \over 2}\,.\]Nápověda – definice
Střední hodnota veličiny A, které přísluší operátor \(\hat A\), ve stavu ψ je dána vztahem
\[\langle A \rangle = \langle \psi| \hat A \psi \rangle =\int_0^L \psi^*(x) \hat A \psi(x) \mathrm{d} x\,.\]Neurčitost A je pak dána vztahem
\[\Delta A = \sqrt{\langle A^2 \rangle - \langle A \rangle^2}\,.\]Operátor souřadnice má v tomto případě tvar
\[\hat x = x\,.\]Operátor hybnosti má v tomto případě tvar
\[\hat p = -i \hbar {\mathrm{d} \over \mathrm{d} x}\,.\]Nápověda – Heisenbergova relace neurčitosti
Heisenbergova relace neurčitosti pro polohu a hybnost má (pro 1D případ) tvar
\[\Delta x \,\cdot\, \Delta p \ge \frac{\hbar}{2}\,.\]Nápověda – užitečné matematické vzorce
Pro urychlení výpočtu využijte znalost integrálů (které si jinak můžete sami lehce odvodit metodou per partes)
\[\int x \,\cos(ax)\, \mathrm{d} x = {x \over a}\, \sin(ax) + {1 \over a^2}\, \cos(ax)\,,\] \[\int x^2 \,\cos(ax) \mathrm{d} x = {x^2 \over a}\, \sin(ax) + {2x \over a^2}\,\cos(ax) - {2 \over a^3}\,\sin(ax)\,.\]Dále také pro úpravu výrazu před integrací užijeme vzorce
\[|\sin\frac{x}{2}|=\sqrt{\frac{1-\cos{x}}{2}}\,,\]neboli jinak zapsaný
\[\sin^2{x}=\frac{1-\cos{2x}}{2}\,.\]Řešení
Nejprve si spočítáme potřebné střední hodnoty. Pro střední hodnotu souřadnice \(\langle x \rangle\) v zadaném stavu platí
\[\langle x \rangle = \int_0^L \psi^*(x) x \psi(x) \mathrm{d} x = {2 \over L} \int_0^L x \sin^2\left({\pi x \over L}\right) \mathrm{d} x = \]přepíšeme druhou mocninu sinu (viz nápověda)
\[={1 \over L} \int_0^L \left( x - x \cos\,{2\pi x \over L} \right) \mathrm{d} x =\]a zintegrujeme, druhý člen pomocí metody per-partes nebo vzorce z nápovědy:
\[={1 \over L} \,\left[ {x^2 \over 2} \,- \,{Lx \over 2\pi}\,\sin\,{2\pi x \over L}\, - \,{L^2 \over 4\pi^2}\,\cos\,{2\pi x \over L} \right]_0^L = {L \over 2}\,.\]Pro střední hodnotu kvadrátu souřadnice \(\langle x^2 \rangle\) platí (postup je stejný jako výše)
\[\langle x^2 \rangle = \int_0^L \psi^*(x) x^2 \psi(x) \mathrm{d} x = {2 \over L} \int_0^L x^2 \,\sin^2\,\left({\pi x \over L}\right) \mathrm{d} x ={1 \over L} \int_0^L \left( x^2 - x^2 \,\cos\,{2\pi x \over L} \right) \mathrm{d} x =\] \[={1 \over L} \,\left[ {x^3 \over 3}\, -\, {Lx^2 \over 2\pi}\,\sin\,{2\pi x \over L} \,-\, {L^2 x \over 2\pi^2}\,\cos\,{2\pi x \over L} + {L^3 \over 4\pi^3}\,\sin\,{2\pi x \over L} \right]_0^L = {L^2 \over 3}\, -\, {L^2 \over 2\pi^2}\,.\]Pro střední hodnotu hybnosti \(\langle p \rangle\) platí
\[\langle p \rangle = \int_0^L \psi^*(x) \left(-i\hbar \right) {\mathrm{d} \psi(x) \over \mathrm{d} x} \mathrm{d} x = -i\hbar {2 \over L}\int_0^L {\pi \over L}\,\sin\,{\pi x \over L}\,\cos\,{\pi x \over L} \mathrm{d} x =\]a zintegrujeme substituční metodou
\[= -i{\hbar \over L} \,\Big[ \sin^2\,\left({\pi x \over L}\right) \Big]_0^L = 0\,.\]Pro střední hodnotu kvadrátu hybnosti \(\langle p^2 \rangle\) platí
\[\langle p^2 \rangle = \int_0^L \psi^*(x) \left(-\hbar^2 \right) \,{\mathrm{d}^2 \psi(x) \over \mathrm{d} x^2} \mathrm{d} x = \hbar^2\, {2\pi^2 \over L^3}\int_0^L \sin^2\,\left({\pi x \over L}\right) \mathrm{d} x = {\pi^2 \,\hbar^2 \over L^3} \int_0^L \left( 1\, -\, \cos{2\pi x \over L} \right) \mathrm{d} x =\] \[= {\pi^2 \hbar^2 \over L^3} \,\left[ x \,-\, {L \over 2\pi}\,\sin\,{2\pi x \over L}\right]_0^L = {\pi^2 \hbar^2 \over L^2}\,.\]Neurčitost polohy částice je rovna
\[\Delta x = \sqrt{\langle x^2 \rangle - \langle x \rangle^2} = \sqrt{{L^2 \over 3} - {L^2 \over 2\pi^2} - {L^2 \over 4}} = {L \over 2\pi}\sqrt{{\pi^2 -6 \over 3}} \approx 0{,}18~L\,.\]Neurčitost hybnosti částice je rovna
\[\Delta p = \sqrt{\langle p^2 \rangle - \langle p \rangle^2} = \sqrt{{\pi^2 \hbar^2 \over L^2}-0} = {\pi \hbar \over L}\,.\]Spočítané hodnoty dosadíme do Heisenbergovy relace neurčitosti
\[\Delta x \,\Delta p = {L \over 2\pi}\sqrt{{\pi^2 -6 \over 3}}\,{\pi \hbar \over L} = \sqrt{{\pi^2 -6 \over 3}} \,{\hbar \over 2} \approx 1{,}14\,~\,{\hbar \over 2}\, > \,{\hbar \over 2}\]a vidíme, že je to v pořádku.
Poznámka
V této úloze stojí za povšimnutí několik věcí. Nejdříve si uvědomme, že neurčitost hybnosti částice \[\mathrm{\Delta} p = {\pi \hbar \over L}\] je nepřímo úměrná šířce jámy, a pro velmi širokou jámu tedy umíme střední hodnotu hybnosti určit velmi přesně. Interval odpovídající střední hodnotě polohy plus/mínus neurčitost polohy, tj. interval x = 0,50 L ± 0,18 L, ve kterém se částice nachází s velkou pravděpodobností, zabírá 36 % celé jámy, což je poměrně dost.
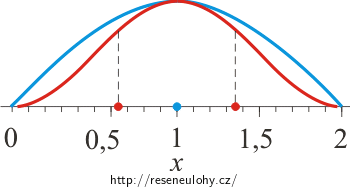
Na obrázku je pro jámu šířky L = 2 AU (viz poznámka níže) modrou čarou vyznačen průběh vlnové funkce základního stavu částice a červenou čarou hustota pravděpodobnosti výskytu částice v daném místě. Bod vyznačený modrým kolečkem odpovídá střední hodnotě souřadnice \(\left< x \right>\), body vyznačené červenými kolečky pak odpovídají této střední hodnotě zmenšené, resp. zvětšené o neurčitost \(\Delta x\).
Poznámka
AU je zkratkou anglických slov arbitrary unit. Pojem arbitrární jednotka zavedli fyzikové pro ilustrativní příklady, jako je tento, v nichž nám jde o poměr mezi veličinami, popis trendu apod. U rozměrů znamená AU libovolnou délkovou jednotku.


