Sbírka řešených úloh

Kreslení vlnové funkce

Úloha číslo: 698

V obecném řešení úlohy Diskrétní spektrum této sbírky jsme zjistili, že vlnová funkce základního stavu částice o hmotnosti m v potenciálové jámě hloubky V₀ umístěné mezi body x = −L/2 a x = L/2

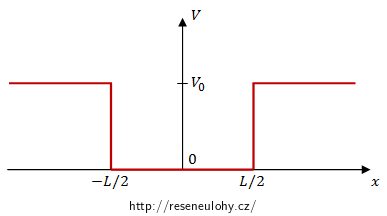
má tvar

\(\psi(x)=Ae^{\alpha x}\) pro x ≤ −L/2,

\(\psi(x)=D\cos(kx)\) pro |x| ≤ L/2,

\(\psi(x)=Ae^{-\alpha x}\) pro x ≥ L/2,

kde k je řešením transcendentní rovnice

\[kL=2\,\mbox{arctg}\sqrt{\frac{2mV_0}{\hbar^2 k^2}\,-\,1} ,\] kde \[\alpha=\sqrt{\frac{2m(V_0-E)}{\hbar^2}}\]

a A, D jsou vhodné normovací konstanty.

Číslo α nazýváme koeficient útlumu (attenuation coefficient). Jeho převrácenou hodnotou je vzdálenost, na níž hodnota exponenciální části vlnové funkce poklesne na jednu e-tinu (decrease length).

 

1) V aplikaci Wave Function Sketcher dostupné na http://phys.educ.ksu.edu/vqm/html/wfsketcher.html „nakreslete” vlnovou funkci základního stavu elektronu v jámě šířky 0,5 nm a hloubky 4 eV. K numerickému řešení využijte Numerical Solution for Ground State dostupné na http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/pfbox.html.

2) Pomocí počitadla pravděpodobnosti výskytu částice v jistých mezích, které je také součástí výše zmíněné aplikace Wave Function Sketcher, zjistěte, s jakou pravděpodobností se elektron v základním stavu v jámě šířky 0,5 nm a hloubky 4 eV nachází v klasicky nedostupné oblasti.

Důležitá poznámka: Wave Function Sketcher pracuje s jámou, jejíž okraj odpovídá nulové potenciální energii a dno záporné potenciální energii. Numerical Solution for Ground State pracuje s jámou, jejíž dno odpovídá nulové potenciální energii tak, jak ukazuje ilustrace v úvodu této úlohy. Jelikož však nulovou hladinu potenciálu můžeme volit libovolně, tyto spíše vizuální rozdíly nemají vliv na stav diskutované částice. Pouze si musíme při přechodu od jednoho případu k druhému dávat pozor, kde dosazovat potenciální energii nulovou, kdy +4 eV a kdy −4 eV.

• Nápověda k 1

  Jako vstupní hodnoty dosaďte do numerického výpočtu dostupného na http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/pfbox.html

  šířku jámy (well width) „L = 0.5 nm”,

  hmotnost (mass) „m = 1 m_e”,

  hloubku jámy (potential U0) „U0 = 4 eV”.

  Z vypočtených údajů můžete vyčíst koeficient útlumu (attenuation coefficient) α, jehož převrácenou hodnotou je vzdálenost, na níž hodnota exponenciální části vlnové funkce poklesne na jednu e-tinu (tj. decrease length, kterou je třeba zadat při „kreslení” vlnové funkce na http://phys.educ.ksu.edu/vqm/html/wfsketcher.html).

• Řešení 1

  „Kreslení” vlnové funkce na http://phys.educ.ksu.edu/vqm/html/wfsketcher.html:

  Parametry jámy nastavíme dle zadání potential width 0.500 nm, height −4.000 eV, right level 0.000 eV.

  Po čtvrté iteraci vychází v Numerical Solution for Ground State efektivní kinetická energie částice asi 0.733 eV. Nastavíme tedy total energy −3.280 eV, což je kinetická energie zmenšená o potenciální energii 4 eV (resp. k ní nejbližší hodnota, kterou diskrétní nastavování hodnot energie umožňuje).

   

  Dále nastavíme parametry vlnové funkce v Regionu II.

  Amplitudu (amplitude) nastavíme rovnou 1.000, aby byla funkce pěkně vidět.

  Po čtvrté iteraci vychází v Numerical Solution for Ground State efektivní šířka jámy rovna 0.716 nm. Vlnovou délku (wavelength) nastavíme rovnou dvojnásobku této šířky, tj. 1.432 nm (uvnitř leží jen „jeden kopeček kosinusoidy”). Tlačítkem check můžeme zkontrolovat, že jsme vlnovou délku určili správně.

  Fázový posun (phase) nastavíme tak, aby nejvyšší bod kosinusoidy ležel ve středu jámy. Vzhledem k diskrétnímu nastavování možných hodnot se nejlepší zdá být hodnota 0.168π (nebo případně 0.176π, přesné by bylo asi něco mezi).

   

  Dále nastavíme parametry vlnové funkce v Regionu I.

  Výběr tvaru křivky (shape) je zřejmý – patří sem rostoucí kladná exponenciála.

  Teď budeme muset trochu počítat. V zadání jsme připomněli, že koeficient útlumu

  \[\alpha=\sqrt{\frac{2m(V_0-E)}{\hbar^2}} .\]

  Jeho převrácenou hodnotou je vzdálenost, na níž hodnota exponenciální části vlnové funkce poklesne na jednu e-tinu (decrease length). Označme ji x_d. Platí

  \[x_d=\frac{1}{\alpha}=\frac{\hbar}{\sqrt{2m(V_0-E)}} .\]

  Dosadíme-li sem hmotnost elektronu, potenciál 4 eV a výše zmíněnou efektivní hodnotu energie (v základních jednotkách, tj. joulech), dostáváme

  \[x_d=\frac{1{,}055\,\cdot\,10^{-34}}{\sqrt{2\,\cdot\,9{,}11\,\cdot\,10^{-31}\,\cdot\,3{,}280\,\cdot\,1{,}602\,\cdot\,10^{-19}}}\ \mbox{m}\,\dot{=}\,0{,}108\ \mbox{nm}.\]

  Tlačítkem check můžeme ověřit, že decrease length rovná 0.108 nm je správně.

  Amplitudu (amplitude) nastavíme tak, aby exponenciála na hranici potenciálové jámy hladce navazovala na část kosinusoidy. Jde přibližně o hodnotu 0.484 nm.

   

  V Regionu III nastavíme parametry vlnové funkce stejně jako v Regionu I, pouze tvar křivky zvolíme jako klesající kladnou exponenciálu.

• Řešení 2

  Hranice oblasti, pro niž je vypočítávána pravděpodobnost výskytu částice, posuneme na hranice jámy. Vidíme, že uvnitř jámy se částice vyskytuje s pravděpodobností 87 %. Úhrnná pravděpodobnost výskytu částice na ose x musí být rovna 100 %, částice se proto mimo jámu (tj. v klasicky nedostupné oblasti) nachází s pravděpodobností 13 %.

• Vizuální řešení

  

    Kliknutím na ikonku vlevo se vám v novém panelu otevře obrázek dvou grafů vytvořených pomocí Wave Function Sketcheru v úkolu 1 této úlohy.