Sbírka řešených úloh

Polovina oscilátoru

Úloha číslo: 2017

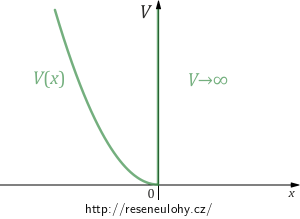
Řešte stacionární Schrödingerovu rovnici pro potenciál \[V(x)\ \ \begin{cases} =\frac{1}{2}m\omega^2x^2 & \quad \text{pro } x<0, \\ \to\infty & \quad \text{pro } x>0.\\ \end{cases}\]

• Nápověda 1

  Zamyslete se, zda zadaný potenciál připomíná nějaký potenciál, jehož řešení již známe.

• Řešení nápovědy 1

  Zadaný potenciál pro \(x<0\) \[{V}=\frac{1}{2}m\omega^2x^2\] je stejný jako potenciál pro lineární harmonický oscilátor, jehož řešení známe.

   

  Řešením stacionární Schrödingerovy rovnice pro lineární harmonický oscilátor \[\left(-\frac{\hbar^2}{2m}\frac{\,\mathrm{d}^2}{\,\mathrm{d}x^2}+\frac{1}{2}m\omega^2x^2\right)\psi(x)=E\psi(x)\] jsou vlastní funkce \[\psi_k=H_k\!\left(\frac{x}{x_0}\right)\mathrm{e}^{-\frac{1}{2}\left(\frac{x}{x_0}\right)^2}\] a energie \[E_k=\hbar\omega\left(k+\frac{1}{2}\right),\] kde \(k\) je přirozené číslo nebo nula, \(H_k\!\left(\frac{x}{x_0}\right)\) jsou tzv. Hermitovy polynomy a konstanta \(x_0=\sqrt{\frac{\hbar}{m\omega}}\).

  Uveďme si několik prvních Hermitových polynomů

  \[H_0\!\left(\frac{x}{x_0}\right)=1,\] \[H_1\!\left(\frac{x}{x_0}\right)=2\frac{x}{x_0},\] \[H_2\!\left(\frac{x}{x_0}\right)=-2+4\left(\frac{x}{x_0}\right)^2,\] \[H_3\!\left(\frac{x}{x_0}\right)=-12\frac{x}{x_0}+8\left(\frac{x}{x_0}\right)^3,\] \[H_4\!\left(\frac{x}{x_0}\right)=12-48\left(\frac{x}{x_0}\right)^2+16\left(\frac{x}{x_0}\right)^4.\]

  Z napsaných Hermitových polynomů je vidět, že Hermitovy polynomy obsahují pro \(k\) sudé jen sudé členy rozvoje (koeficienty u lichých členů jsou nulové) a pro \(k\) liché jen liché členy. Tedy pouze Hermitovy polynomy pro sudá \(k\) obsahují absolutní člen \(c_0\left(\frac{x}{x_0}\right)^0.\)

• Nápověda 2

  Promyslete, jak bychom mohli využít toho, že známe řešení pro lineární harmonický oscilátor.

• Řešení nápovědy 2

  Uvědomme si, že stacionární Schrödingerova rovnice je diferenciální rovnice, kterou budeme řešit na jednotlivých intervalech hodnot souřadnice \(x\). Pokud na některém intervalu je potenciál stejný jako potenciál lineárního harmonického oscilátoru, tak i řešení na tomto intervalu musí mít stejný tvar. Rovnici tedy řešit nemusíme, protože řešení již známe.

• Nápověda 3

  Známe již řešení Schrödingerovy rovnice pro zadaný potenciál na otevřených intervalech. Zvažte, zda toto řešení můžeme považovat za konečný výsledek. Uvědomte si, jaké jsou požadavky na vlnovou funkci.

• Řešení nápovědy 3

  Známe-li řešení Schrödingerovy rovnice pro daný potenciál na dvou intervalech, je potřeba obě řešení napojit v hraničním bodě, protože vlnová funkce musí být spojitá. Z důvodu nekonečně velkého skoku potenciální energie v hraničním bodě (tj. v bodě \(x=0\)) netrváme zde na spojitosti derivace vlnové funkce.

• Řešení

  Nejprve si všimneme, že potenciál je zadaný různě na dvou intervalech \[ V(x) \begin{cases} =\frac{1}{2}m\omega^2x^2 & \quad \text{pro } x<0,\\ \to\infty & \quad \text{pro } x>0.\\ \end{cases}\] Pro \(x<0\) je potenicál stejný jako potenciál pro lineární harmonický oscilátor, pro \(x>0\) je potenciál nekonečný.

  Stacionární Schrödingerovu rovnici budeme řešit na každém intervalu zvlášť. V místech, kde se potenciál blíží k nekonečnu, se částice nemůže vyskytovat. Vlnová funkce je zde tedy nulová. Řešení stacionární Schrödingerovy rovnice pro \(x<0\) je stejné jako řešení pro lineární harmonický oscilátor. Souhrnně tedy můžeme psát

  \[ \psi_k(x)= \begin{cases} H_k\!\left(\frac{x}{x_0}\right)\mathrm{e}^{-\frac{1}{2}\left(\frac{x}{x_0}\right)^2} & \quad \text{pro } x<0,\\ 0 & \quad \text{pro } x>0.\\ \end{cases}\]

  Funkce \(\psi_k(x)\) musí být spojitá ve všech bodech, speciálně musíme zajistit spojitost v bodě \(x=0\), z čehož vyplývá požadavek \[\psi_k(0)=0.\]

  Zamysleme se nad tím, jaké hodnoty dostaneme, pokud se \(x\) blíží k nule zleva. Do řešení pro lineární harmonický oscilátor lze přímo dosadit \(x=0\). Hodnota výrazu \(\mathrm{e}^{-\frac{1}{2}\left(\frac{x}{x_0}\right)^2}\) je rovna jedné. Hodnota Hermitova polynomu \(H_k\!\left(\frac{x}{x_0}\right)\) je rovna pro sudá \(k\) jeho absolutnímu členu, jež je nenulový. Tedy pouze Hermitovy polynomy pro lichá \(k\) jsou pro \(x=0\) nulové (viz Řešení nápovědy 1). Abychom se nemuseli při číslování řešení omezovat pouze na lichá čísla, ale mohli použít všechna přirozená čísla, zvolíme index \(n\), pro který bude platit \(k=2n+1\).

  Řešením stacionární Schrödingerovy rovnice pro zadaný potenciál \(V\) jsou vlnové funkce \[\varphi_n(x)= \begin{cases} H_{2n+1}\!\left(\frac{x}{x_0}\right)\mathrm{e}^{-\frac{1}{2}\left(\frac{x}{x_0}\right)^2} & \quad \text{pro } x<0,\\ 0 & \quad \text{pro } x\geq 0,\\ \end{cases}\] kde \(n\) je libovolné přirozené číslo nebo nula, \(H_{2n+1}\!\left(\frac{x}{x_0}\right)\) jsou Hermitovy polynomy a konstanta \(x_0=\sqrt{\frac{\hbar}{m\omega}}\). Energie tohoto stavu je rovna \[ E_n(x) = \hbar\omega\left(2n+1+\frac{1}{2}\right) = \hbar \omega \left(2n+\frac{3}{2}\right). \]

• Odpověď

  Řešení stacionární Schrödingerovy rovnice pro potenciál \[V(x) \begin{cases} =\frac{1}{2}m\omega^2x^2 & \quad \text{pro } x<0, \\ \to\infty & \quad \text{pro } x>0\\ \end{cases}\] jsou vlnové funkce \[\varphi_n(x)= \begin{cases} H_{2n+1}\!\left(\frac{x}{x_0}\right)\mathrm{e}^{-\frac{1}{2}\left(\frac{x}{x_0}\right)^2} & \quad \text{pro } x<0, \\ 0 & \quad \text{pro } x\geq 0,\\ \end{cases}\] a energie \[ E_n(x) =\hbar\omega\left(2n+\frac{3}{2}\right)\] kde \(n\) je přirozené číslo, \(H_{2n+1}\!\left(\frac{x}{x_0}\right)\) jsou Hermitovy polynomy a konstanta \(x_0=\sqrt{\frac{\hbar}{m\omega}}\).