Určení Planckovy konstanty a výstupní práce z experimentálních dat pro fotoelektrický jev
Úloha číslo: 626
Z následujících hodnot naměřených při vnějším fotoelektrickém pokusu na lithiu určete Planckovu konstantu a výstupní práci pro lithium. Získané hodnoty porovnejte s hodnotami uvedenými v tabulkách.
| vlnová délka záření λ [nm] | 433,9 | 404,7 | 365,0 | 312,5 | 253,5 |
| brzdné napětí U [V] | 0,55 | 0,73 | 1,09 | 1,67 | 2,57 |
Nápověda
Pro řešení úlohy je třeba znát Einsteinovu rovnici fotoelektrického jevu, která určuje maximální kinetickou energii Ek uvolněných elektronů:
\[E_k=hf-W_v ,\]kde součin Planckovy konstanty h a frekvence záření f je roven energii jednoho dopadajícího fotonu a Wv je tzv. výstupní práce (konstanta charakterizující daný kov).
Tato rovnice nám říká, že mezi frekvencí záření a maximální kinetickou energií vyletujících elektronů je lineární vztah. Nejjednoduší proto bude přepočítat zadané vlnové délky na frekvence a z brzdného napětí určit kinetickou energií elektronů. tyto hodnoty vynést do grafu, proložit přímkou a z její rovnice určit hledané konstanty.
Prokládání přímky – lineární regresi – můžete udělat jak s papírem a kalkulačkou, tak to můžete svěřit vhodnému programu, např. MS Excel.
Rozbor
Při fotoelektrickém jevu pozorujeme, že pokud dopadá na kov světlo (či obecněji elektromagnetické záření) může za určitých podmínek uvolňovat z kovu elektrony, které tvoří tzv. fotoelektrický proud. Tento jev vysvětlil A. Einstein a sestavil tzv. Einsteinovu rovnici fotoelektrického jevu, která určuje maximální kinetickou energii Ek uvolněných elektronů.
Maximální kinetickou energii elektronů měříme pomocí brzdného napětí, tj. měřením napětí, které již žádný uvolněný elektron není schopen překonat. Práce, kterou vykonají elektrické síly, když elektron překonává toto napětí, se rovná kinetické energii, se kterou byl z kovu uvolněn.
Výstupní práce a Planckova konstanta v tomto zákonu vystupují a určíme je porovnáním naměřených hodnot a teoretického vztahu.
Řešení
Einsteinova rovnice fotoelektrického jevu, která určuje maximální kinetickou energii Ek uvolněných elektronů, zní:
\[E_k=hf-W_v ,\]kde součin Planckovy konstanty h a frekvence záření f je roven energii jednoho dopadajícího fotonu a Wv je tzv. výstupní práce (konstanta charakterizující daný kov).
Maximální kinetická energie elektronu Ek se rovná práci, kterou vykonají elektrické síly, když elektron překonává tzv. brzdné napětí. Elektrická práce je dána součinem náboje elektronu e a napětí U, tj. platí
\[E_k=eU ,\]kde e = 1,6·10−19 C je elementární náboj.
Z naměřených dat si vypočteme kinetické energie elektronů a frekvence záření, tj. veličiny, které vystupují v Einsteinově rovnici:
vlnová délka záření λ [nm] 433,9 404,7 365,0 312,5 253,5 frekvence zářeni f [Hz] 6,914·1014 7,413·1014 8,219·1014 9,600·1014 11,834·1014 brzdné napětí U [V] 0,55 0,73 1,09 1,67 2,57 max. kin. energie elektronu Ek [J] 0,880·10−19 1,168·10−19 1,744·10−19 2,672·10−19 4,112·10−19 Dopočítané hodnoty si vyneseme do grafu:
Zdrojový soubor (MS Excel)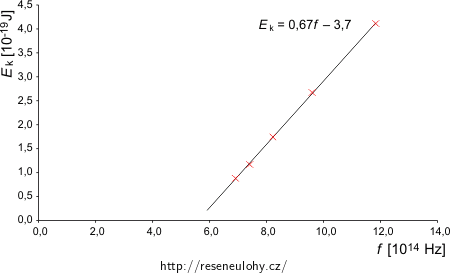
Z grafu vidíme, že naměřené hodnoty opravdu leží na přímce, jak předpovídá Einsteinova rovnice (tvoří lineární funkci). Proložíme jimi přímku a necháme si zobrazit její rovnici (např. v programu MS Excel vložíme lineární spojnici trendu).
Na vodorovné ose je frekvence f, tj. místo x budeme psát f a místo y kinetickou energii Ek, která je na svislé ose. Dosadíme také násobky jednotek, které jsme při sestrojování grafu použili. Dostáváme tedy rovnici:
\[\frac{E_{\mathrm{k}}}{10^{-19}\,\mathrm{J}}=0{,}6616\frac{f}{10^{14}\,\mathrm{Hz}}-3{,}7039,\]tuto rovnici upravíme a dosadíme vztah 1 Hz = 1 s−1
\[E_{\mathrm{k}}=\frac{0{,}6616{\cdot}10^{-19}\,\mathrm{J}}{10^{14}\,\mathrm{Hz}}f-3{,}7039{\cdot}10^{-19}\,\mathrm{J}\] \[E_{\mathrm{k}}=6{,}6{\cdot}10^{-34}\,\mathrm{Js}\,f-3{,}7{\cdot}10^{-19}\,\mathrm{J}.\]Když porovnáme získaný vztah s obecnou Einsteinovou rovnicí, vidíme, že jsme získali:
h = 6,6·10−34 JsWv = 3,7·10−19 J.Získaná Planckova konstanta h dobře odpovídá tabulkové hodnotě.
Dále v tabulkách nalezneme, že výstupní práce Wv pro litium je 2,36 eV. Použijeme-li převodní vztah mezi jednotkami energie 1 eV = 1,6·10−19 J, dostáváme, že
Wv = 2,36 eV = 2,36·1,6·10−19 J = 3,8·10−19 J,což také celkem dobře odpovídá nalezené hodnotě.
Odpověď
Z naměřených dat jsme získali Planckovu konstantu h = 6,6·10−34 Js a výstupní práci pro lithium Wv = 3,7·10−19 J. Oba údaje dobře odpovídají tabulkovým hodnotám.




