Sbírka řešených úloh

Diskrétní spektrum

Úloha číslo: 709

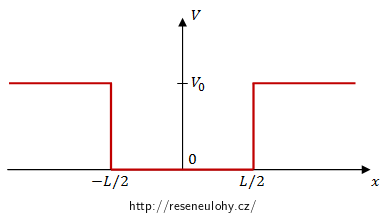
Uvažujte elektron v potenciálové jámě hloubky V₀ = 1,25 eV a šířky L = 14,5 nm.

a) Určete počet diskrétních energetických hladin pro tento případ.

b) Určete přibližně dvě nejnižší hladiny energie.

• Nápověda

  Stacionární Schrödingerova rovnice pro vlnovou funkci ψ popisující stav částice o hmotnosti m a energii E má tvar

  \[\frac{\mbox{d}^2 \psi}{\mbox{d}x^2}\,+\,\frac{2m(E-V(x))}{\hbar^2}\,\psi=0\,.\]

  Vzhledem k průběhu potenciálu je v tomto případě vhodné přepsat si tuto rovnici zvlášť pro tři oblasti tak, jak je znázorněno v následujícím obrázku.

  

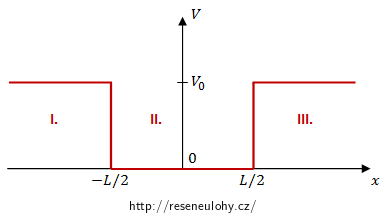
  Vlnová funkce musí být v bodech x = ± L/2 (tj. v místech s konečnou nespojitostí potenciálu) spojitá a mít v nich spojitou první derivaci. Je nutno splnit tzv. sešívací podmínky:

  \[\psi_I\left(-L/2\right)=\psi_{II}\left(-L/2\right)\,,\] \[\psi_{II}\left(L/2\right)=\psi_{III}\left(L/2\right)\,,\] \[\frac{\mbox{d}\psi_I}{\mbox{d}x}\left(-L/2\right)=\frac{\mbox{d}\psi_{II}}{\mbox{d}x}\left(-L/2\right)\,,\] \[\frac{\mbox{d}\psi_{II}}{\mbox{d}x}\left(L/2\right)=\frac{\mbox{d}\psi_{III}}{\mbox{d}x}\left(L/2\right)\,.\]

  Splněny musí být také okrajové podmínky:

  \[\lim_{x \rightarrow -\infty}\psi_I(x)=0\ \ \mbox{a}\ \ \lim_{x \rightarrow \infty}\psi_{III}(x)=0\,.\]

• Obecné řešení

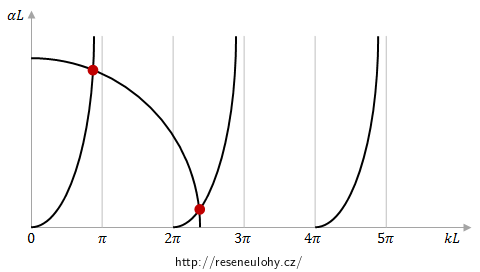
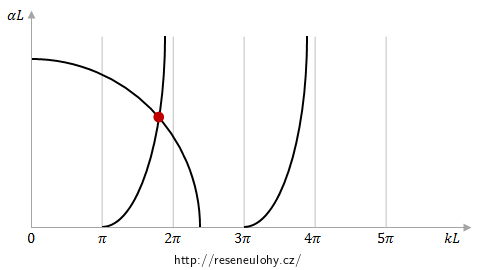
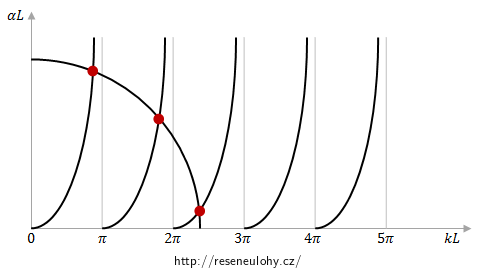
  Obecné řešení provedeme ve čtyřech krocích. Nejprve vyřešíme Schrödingerovu rovnici pro danou situaci postupně v oblastech I, II a III. Ze symetrie problému vzhledem k bodu x = 0 vyplývá i určitá symetrie vlastních funkcí hamiltoniánu. Postupně tedy budeme diskutovat sudé a následně liché vlastní funkce. V závěru obecného řešení shrneme vlastní čísla příslušná sudým i lichým vlastním funkcím a provedeme krátkou diskusi o diskrétním energetickém spektru pro danou situaci.

• Řešení Schrödingerovy rovnice

  Vzhledem k průběhu potenciálu je v tomto případě vhodné řešit Schrödingerovu rovnici zvlášť pro tři oblasti tak, jak je znázorněno v následujícím obrázku.

  

  Pro energii E < V₀ má nečasová Schrödingerova rovnice v oblasti I tvar

  \[\frac{\mbox{d}^2 \psi_I}{\mbox{d}x^2}\,+\,\frac{2m(E-V_0)}{\hbar^2}\,\psi_I=0\] \[\frac{\mbox{d}^2 \psi_I}{\mbox{d}x^2}\,-\,\alpha^2\,\psi_I=0\,,\]

  kde

  \[\alpha=\sqrt{\frac{2m(V_0-E)}{\hbar^2}}\,>\,0\,.\]

  Obecné řešení této diferenciální rovnice má tvar

  \[\psi_I=Ae^{\alpha x}\,+\,Be^{-\alpha x}\,,\]

  kde A, B jsou libovolná komplexní čísla. Vzhledem k okrajové podmínce pro x → −∞ má však fyzikální smysl pouze \(\psi_I=Ae^{\alpha x}\).

   

  Analogicky dostaneme v oblasti III obecné řešení

  \[\psi_{III}=Fe^{\alpha x}\,+\,Ge^{-\alpha x}\,,\]

  kde F, G jsou libovolná komplexní čísla. Vzhledem k okrajové podmínce pro x → ∞ má však fyzikální smysl pouze \(\psi_{III}=Ge^{-\alpha x}\).

   

  V oblasti II má Schrödingerova rovnice tvar

  \[\frac{\mbox{d}^2 \psi_{II}}{\mbox{d}x^2}\,+\,\frac{2mE}{\hbar^2}\,\psi_{II}=0\] \[\frac{\mbox{d}^2 \psi_{II}}{\mbox{d}x^2}\,+\,k^2\,\psi_I=0\,,\]

  kde

  \[k=\sqrt{\frac{2mE}{\hbar^2}}\,>\,0\,.\]

  Obecné řešení této diferenciální rovnice má tvar

  \[\psi_{II}=C\,\sin(kx)\,+\,D\,\cos(kx)\,,\]

  kde C, D jsou libovolná komplexní čísla.

  Ze symetrie potenciálu vzhledem k bodu x = 0 lze odvodit, že vlastní funkce hamiltoniánu musí být buď sudé, nebo liché. (Detailně viz např. SKÁLA, L. Úvod do kvantové mechaniky. Praha: Academia, 2005, s. 98. ISBN 80-200-1316-4.)

  Sudé jsou funkce \(\psi_{II}=D\,\cos(kx)\) a liché funkce \(\psi_{II}=C\,\sin(kx)\).

• Sudá řešení

  Mějme neprve vlnovou funkci sestávájící z

  \(\psi_{I}(x)=Ae^{\alpha x}\) pro x ≤ −L/2,

  \(\psi_{II}(x)=D\cos(kx)\) pro |x| < L/2,

  \(\psi_{III}(x)=Ge^{-\alpha x}\) pro x ≥ L/2.

  Vzhledem k symetrii problému musí být G = A a stačí, když budeme situaci dále řešit pouze pro x ≥ 0. Vzhledem ke spojitosti vlnové funkce (viz nápověda) musí platit

  \[\ \psi_{II}\left(\frac{L}{2}\right)= \psi_{III}\left(\frac{L}{2}\right)\] \[\frac{\mbox{d}\psi_{II}}{\mbox{d}x}\left(\frac{L}{2}\right)=\frac{\mbox{d}\psi_{III}}{\mbox{d}x}\left(\frac{L}{2}\right)\,,\]

  tj. po dosazení

  \[D\,\cos\left(\frac{kL}{2}\right)=Ae^{-\frac{\alpha L}{2}}\] \[-kD\,\sin\left(\frac{kL}{2}\right)=-\alpha Ae^{-\frac{\alpha L}{2}}\]

  neboli

  \[e^{-\frac{\alpha L}{2}}A\,-\,\cos\left(\frac{kL}{2}\right)D=0\] \[\alpha e^{-\frac{\alpha L}{2}}A\,-\,k\,\sin\left(\frac{kL}{2}\right)D=0\,.\]

  Aby měla tato homogenní soustava dvou lineárních rovnic o dvou neznámých A, D netriviální řešení, musí být její determinant roven nule:

  \[-e^{-\frac{\alpha L}{2}}k\,\sin\left(\frac{kL}{2}\right)\,+\,\alpha e^{-\frac{\alpha L}{2}}\cos\left(\frac{kL}{2}\right)=0\,.\]

  Hledáme tedy taková k, pro která se výraz na levé straně vynuluje. Po jednoduché úpravě dostáváme podmínku

  \[\mbox{tg}\left(\frac{kL}{2}\right)=\frac{\alpha}{k}=\sqrt{\frac{V_0}{E}\,-\,1}=\sqrt{\frac{2mV_0}{\hbar^2 k^2}\,-\,1}\]

  nebo ekvivalentně

  \[kL=2\,\mbox{arctg}\sqrt{\frac{2mV_0}{\hbar^2 k^2}\,-\,1}\,+\,2n\pi\,,\]

  kde n je celé číslo. Vzhledem k úvodní substituci \(k=\sqrt{\frac{2mE}{\hbar^2}}\,>\,0\) ekvivalentní s \(E=\frac{\hbar^2 k^2}{2m}\) nám už v této chvíli vyvstává před očima nutné kvantování energie.

  Z definice konstant k a α dále vidíme, že platí

  \[k^2\,+\,\alpha^2=\frac{2mV_0}{\hbar^2}\] \[(kL)^2\,+\,(\alpha L)^2=\frac{2mV_0 L^2}{\hbar^2}\,.\]

  Problém teď můžeme řešit graficky, vyneseme-li do soustavy souřadnic s osami kL a αL „kladnou” čtvrtkružnici

  \[(kL)^2\,+\,(\alpha L)^2=\frac{2mV_0 L^2}{\hbar^2}\]

  a křivky

  \[kL=2\,\mathrm{arctg}\,\sqrt{\frac{2mV_0}{\hbar^2 k^2}\,-\,1}\,+\,2n\pi=2\,\mathrm{arctg}\,\left( \frac{\alpha \hbar}{\sqrt{2mE}}\right)\,+\,2n\pi\,.\]

  Obrázek bude vypadat nějak takto:

  

  Počet červeně zvýrazněných průsečíků závisí na poloměru kružnice, který se odvíjí od šířky jámy a dalších parametrů, které vystupují v rovnici této kružnice. Zároveň platí rovnost

  \[\textrm{počet průsečíků} = \textrm{počet}\,k = \textrm{počet diskrétních energetických hladin v dané jámě}.\]

• Lichá řešení

  Mějme nyní vlnovou funkci sestávájící z

  \(\psi_{I}(x)=Ae^{\alpha x}\) pro x ≤ −L/2,

  \(\psi_{II}(x)=C\sin(kx)\) pro |x| < L/2,

  \(\psi_{III}(x)=Ge^{-\alpha x}\) pro x ≥ L/2.

  Vzhledem k symetrii problému musí být G = A a stačí, když budeme situaci dále řešit pouze pro x ≥ 0. Vzhledem ke spojitosti vlnové funkce (viz nápověda) musí platit

  \[\psi_{II}\left(\frac{L}{2}\right)= \psi_{III}\left(\frac{L}{2}\right)\] \[\frac{\mbox{d}\psi_{II}}{\mbox{d}x}\left(\frac{L}{2}\right)=\frac{\mbox{d}\psi_{III}}{\mbox{d}x}\left(\frac{L}{2}\right)\,,\]

  tj. po dosazení

  \[C\,\sin\left(\frac{kL}{2}\right)=Ae^{-\frac{\alpha L}{2}}\] \[kC\,\cos\left(\frac{kL}{2}\right)=-\alpha Ae^{-\frac{\alpha L}{2}}\]

  neboli

  \[\ \ \ e^{-\frac{\alpha L}{2}}A\,-\,\sin\left(\frac{kL}{2}\right)C=0\] \[\alpha e^{-\frac{\alpha L}{2}} A\,+\,k\,\cos\left(\frac{kL}{2}\right)C=0\,.\]

  Aby měla tato homogenní soustava dvou lineárních rovnic o dvou neznámých A, C netriviální řešení, musí být její determinant roven nule:

  \[e^{-\frac{\alpha L}{2}}k\,\cos\left(\frac{kL}{2}\right)\,+\,\alpha e^{-\frac{\alpha L}{2}}\sin\left(\frac{kL}{2}\right)=0\,.\]

  Hledáme tedy taková k, pro která se výraz na levé straně vynuluje. Po jednoduché úpravě dostáváme podmínku

  \[-\mathrm{cotg}\,\left(\frac{kL}{2}\right)=\frac{\alpha}{k}=\sqrt{\frac{V_0}{E}\,-\,1}=\sqrt{\frac{2mV_0}{\hbar^2 k^2}\,-\,1}\]

  nebo ekvivalentně

  \[kL=-2\,\mathrm{arccotg}\,\sqrt{\frac{2mV_0}{\hbar^2 k^2}\,-\,1}\,+\,2n\pi\,,\]

  kde n je celé číslo. Vzhledem k úvodní substituci \(k=\sqrt{\frac{2mE}{\hbar^2}}\,>\,0\) ekvivalentní s \(E=\frac{\hbar^2 k^2}{2m}\) nám už v této chvíli vyvstává před očima nutné kvantování energie.

  Z definice konstant k a α dále vidíme, že platí

  \[k^2\,+\,\alpha^2=\frac{2mV_0}{\hbar^2}\] \[(kL)^2\,+\,(\alpha L)^2=\frac{2mV_0 L^2}{\hbar^2}\,.\]

  Problém teď můžeme řešit graficky, vyneseme-li do soustavy souřadnic s osami kL a αL „kladnou” čtvrtkružnici

  \[(kL)^2\,+\,(\alpha L)^2=\frac{2mV_0 L^2}{\hbar^2}\]

  a křivky

  \[kL=-2\,\mathrm{arccotg}\,\sqrt{\frac{2mV_0}{\hbar^2 k^2}\,-\,1}\,+\,2n\pi=-2\,\mathrm{arccotg}\,\left( \frac{\alpha \hbar}{\sqrt{2mE}}\right)\,+\,2n\pi\,.\]

  Obrázek bude vypadat nějak takto:

  

  Počet červeně zvýrazněných průsečíků závisí na poloměru kružnice, který se odvíjí od šířky jámy a dalších parametrů, které vystupují v rovnici této kružnice. Zároveň platí rovnost

  \[\textrm{počet průsečíků} = \textrm{počet}\,k = \textrm{počet diskrétních energetických hladin v dané jámě}.\]

• Diskrétní hladiny energie

  Teď můžeme grafická řešení obou případů spojit do jednoho obrázku, čímž dostaneme

  

  Počet průsečíků N (a tedy i počet diskrétních hladin energie) závisí na poloměru čtvrtkružnice

  \[r=\sqrt{\frac{2mV_0 L^2}{\hbar^2}}\,.\]

  Zřejmě platí

  \[(N-1)\pi\,<\,r=\sqrt{\frac{2mV_0 L^2}{\hbar^2}}\,<\,N\pi\,.\]

• Řešení a)

  Počet diskrétních energetických hladin N je dán vztahem (viz obecné řešení výše)

  \[(N-1)\pi\,<\,\sqrt{\frac{2mV_0 L^2}{\hbar^2}}\,<\,N\pi\,,\]

  neboli

  \[N-1\,<\,\frac{L\sqrt{2mV_0} }{\pi\hbar}\,<\,N\,.\]

  Po dosazení konkrétních hodnot dostáváme

  \[\frac{L\sqrt{2mV_0} }{\pi\hbar}=\frac{14{,}5\,\cdot\,10^{-9}\,\sqrt{2\,\cdot\,9{,}11\,\cdot\,20^{-31}\,\cdot\,1{,}25\,\cdot\,1{,}602\,\cdot\,10^{-19}}}{\pi\,\cdot\,1{,}055\,\cdot\,10^{-34}}\,\dot{=}\, 26{,}4\,.\]

  Bude tedy N = 27.

• Řešení b)

  Pro přesné určení dvou nejnižších hladin diskrétního energetického spektra bychom museli vyřešit transcendentní rovnice, tj. využít pomoci některého výpočetního matematického programu. Zjistili jsme ale, že v daném případě se v jámě nachází 27 vázaných stavů, což je relativně hodně, a proto první dva průsečíky (viz grafy uvedené v předcházejících sekcích řešení) se zleva dosti blíží bodům, pro které platí kL = π, resp. kL = 2π.

  Hledané hladiny se proto budou blížit energiím

  \[E_1 = \frac{\hbar^2}{2m}\left(\frac{\pi}{L}\right)^2=\frac{\hbar^2 \pi^2}{2mL^2}\]

  a

  \[E_2 = \frac{\hbar^2}{2m}\left(\frac{2\pi}{L}\right)^2=\frac{2\hbar^2 \pi^2}{mL^2}\,,\]

  v nichž poznáváme hladiny energie pro částici o hmotnosti m v nekonečně hluboké potenciálové jámě šířky L (viz úloha Symetrická nekonečná pravoúhlá jáma této sbírky).

• Odpovědi

  a) Pro elektron v potenciálové jámě hloubky V₀ = 1,25 eV a šířky L = 14,5 nm existuje 27 diskrétních energetických hladin.

  b) Hladiny energie prvních dvou vázaných stavů se zdola blíží energiím

      \(E_1 =\frac{\hbar^2 \pi^2}{2mL^2}\,\dot{=}\, 1{,}8\ \mbox{meV}\) a \(E_2 =\frac{2\hbar^2 \pi^2}{mL^2}\,\dot{=}\, 7{,}2\ \mbox{meV}.\)