Sbírka řešených úloh

Změna rozměru nekonečně hluboké potenciálové jámy

Úloha číslo: 2300

• Nápověda 1

  Vyhledejte tvar vlnové funkce n-tého stavu částice s hmotností \(m\) v nekonečně hluboké potenciálové jámě délky \(L\). Vyhledejte i příslušné energie.

• Řešení nápovědy 1

  Vlastní vlnové funkce n-tého stavu částice o hmotnosti \(m\) v nekonečně hluboké potenciálové jámě délky \(L\) a příslušné energie jsou

  \[\psi_n(x)=\sqrt{\frac{2}{L}}\mathrm{sin}\frac{n\pi x}{L},\,\,\,0\leq x\leq L,\] \[E_n=\frac{n^2\pi^2\hbar^2}{2mL^2}, \,\,\,n\in \mathbb{N}.\]

• Nápověda 2

  Vyhledejte, jak se vypočítá pravděpodobnost naměření vlastního čísla příslušného operátoru \(\hat{F}\) ve stavu popsaném vlnovou funkcí \(\psi\).

• Řešení nápovědy 2

  Je-li stav popsán normovanou vlnovou funkcí \(\psi\), kterou rozložíme na lineární kombinaci navzájem kolmých a normovaných vlastních vlnových funkcí \(\psi_i\) operátoru \(\hat{F}\), tj.

  \[\psi=\sum_{i}c_i\psi_i,\]

  tak pravděpodobnost \(P_{\lambda_i}\) naměření vlastního čísla \(\lambda_i\) (příslušný vlastní stav je popsán vlnovou funkcí \(\psi_i\)) je roven

  \[P_{\lambda_i}=|c_i|^2.\]

  Koeficienty \(c_i\) můžeme vypočítat pomocí skalárního součinu

  \[c_i=\left\langle\psi_i|\psi\right\rangle=\int_{−\infty}^{\infty}\psi_i^{*}(x)\psi(x)\,\mathrm{d}x.\]

• Řešení

  Uvažujeme-li nekonečně rychlou změnu rozměru jámy z \(L\) na \(2L\), pak předpokádáme, že částice a tedy i její vlnová funkce „nestihne“ zareagovat na tyto změny. Tedy po této změně zůstane částice ve stavu \(\psi_n\)

  \[\psi_n(x)=\left\{\begin{matrix} \sqrt{\frac{2}{L}}\mathrm{sin}\frac{n\pi x}{L},\,\,\,0\leq x\leq L,\\ 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,L\leq x\lor x\leq 0. \end{matrix}\right.\]

  Graf této funkce je znázorněn v následujícím obrázku.

  

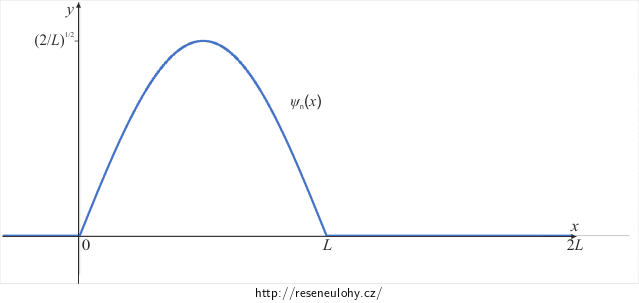
  Tento stav již není vlastním stavem nové jámy, dokonce není ani přípustným stavem, protože je popsán vlnovou funkcí, která uvnitř jámy obsahuje bod, kde funkce není hladká, a to není přípustné. Chápejme tedy tuto úlohu jako modelový příklad a i přes zmíněnou námitku úlohu dopočítejme.

  Vlastní stavy \(\phi_{n'}\) a povolené energie \(E_{n'}\) nové jámy mají tvar

  \[\phi_{n'}(x)=\sqrt{\frac{1}{L}}\mathrm{sin}\frac{{n'}\pi x}{2L},\,\,\,0\leq x\leq 2L, \] \[E_{n'}=\frac{{n'}^2\pi^2\hbar^2}{2m{(2L)}^2}, \,\,\,{n'}\in \mathbb{N}.\]

  Položíme-li rovnu energie částice v původní jámě \(E_n\) a energii částice v nové jámě \(E_{n'}\), dostaneme

  \[\frac{{n}^2\pi^2\hbar^2}{2m{L}^2}=\frac{{n'}^2\pi^2\hbar^2}{2m{(2L)}^2}\quad\Rightarrow \quad n'=2n.\]

  Tedy stejnou energii mají v nové jámě stavy s dvojnásobným kvantovým číslem. Těmto energiím příluší vlastní stavy \(\phi_{2n}\). Tedy hledaný koeficient z lineární kombinace rozkladu původního stavu do báze nových vlastních stavů s energií \(E_n\) je roven

  \[c=\left\langle\phi_{2n}(x)\Big|\psi_n(x)\right\rangle=\int_{−\infty}^{\infty}\phi_{2n}^{*}(x)\psi_n(x)\,\mathrm{d}x=\frac{\sqrt{2}}{L}\int_{0}^{L}\mathrm{sin}^2\frac{n\pi x}{L}\,\mathrm{d}x=\frac{\sqrt{2}}{L}\int_{0}^{L}\frac{1−\mathrm{cos}\frac{2n\pi x}{L}}{2}\,\mathrm{d}x=\] \[=\frac{\sqrt{2}}{L}\left[\frac{x}{2}−\frac{L}{4n\pi}\mathrm{sin}\frac{2n\pi x}{L}\right]_{0}^{L}=\frac{\sqrt{2}}{2}.\]

  A tedy pravděpodobnost nalezení částice ve vlastním stavu \(\phi_{2n}\), tedy se stejnou energií \(E_n\) jako měla před změnou je

  \[P=|c|^2=\frac{1}{2}.\]

• Odpověď

  Uvažujeme-li částici s hmotností \(m\) v nekonečně hluboké pravoúhlé potenciálové jámě délky \(L\) ve vlastním stavu \(\psi_n\) a změnu rozměru jámy na \(2L\), poté pravděpodobnost, že se systém po této změně bude nacházet ve stavu se stejnou energií je rovna

  \[P=\frac{1}{2}.\]