Sbírka řešených úloh

Nestacionární stav, měření energie a časový vývoj stavu

Úloha číslo: 2013

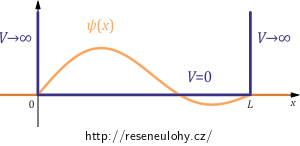
Částice v jednorozměrné pravoúhlé nekonečně hluboké potenciálové jámě v intervalu \((0, L)\) se v čase \(t=0 \mathrm s\) nachází ve stavu popsaném vlnovou funkcí \[\psi(x, t=0 \mathrm s)=N\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right].\]

a) Vlnovou funkci normujte.

b) Rozložte tento stav na stacionární stavy.

c) Určete, jaké hodnoty energie je možné v tomto stavu naměřit a s jakou pravděpodobností.

d) Určete střední hodnotu energie v tomto stavu.

e) Napište tuto vlnovou funkci v obecném čase \(t\) a v čase \(t=\frac{\pi \hbar}{E_1},\) kde \(E_1\) je energie základního stavu.

• Nápověda a)

  Uvědomte si, že normovaná vlnová funkce musí splňovat normovací podmínku.

• Řešení nápovědy a)

  Normovanou vlnovou funkci \(\psi\) zapíšeme ve tvaru \[\psi=N\varphi,\] kde \(N\) je normalizační konstanta a \(\varphi\) je nenormovaná vlnová funkce.

  Normovaná vlnová funkce \(\psi\) musí splňovat normovací podmínku \[<\psi| \psi>=1.\] Hledáme tedy obecně komplexní normalizační konstantu \(N\) splňující normovací podmínku \[1=<\psi| \psi>=\int_{-\infty}^\infty{\psi^\ast\psi}\,\mathrm{d}x=\int_{-\infty}^\infty{N^\ast\varphi^\ast N\varphi}\,\mathrm{d}x=N^\ast N\int_{-\infty}^\infty{\varphi^\ast \varphi}\,\mathrm{d}x=|N|^2\int_{-\infty}^\infty{\varphi^\ast\varphi}\,\mathrm{d}x.\] Odtud vyjádříme velikost normalizační konstanty \[|N|=\sqrt{\frac{1}{\int_{-\infty}^\infty{\varphi^\ast\varphi}\,\mathrm{d}x}}.\] Normalizační konstanta \(N\) však není určena jednoznačně, zjistili jsme pouze její velikost. Z důvodu zjednodušení výpočtů se obvykle normalizační konstanta \(N\) volí reálná kladná.

• Nápověda b), c)

  Při řešení úlohy rozložíme zadaný obecný stav částice \(\psi\) v jednorozměrné pravoúhlé potenciálové jámě na lineární kombinaci stacionárních stavů. Připomeňte si, jaké má řešení stacionární Schrödingerova rovnice pro jednorozměrnou pravoúhlou nekonečně hlubokou potenciálovou jámu, tedy v jakém tvaru napíšeme stacionární stavy a energie.

  Promyslete si, jak souvisí rozklad obecného stavu na stacionární stavy s pravděpodobností naměření energie.

• Řešení nápovědy b), c)

  Řešením stacionární Schrödingerovy rovnice \[\hat{H}\varphi_n(x)=E_n\varphi_n(x)\] pro částici v jednorozměrné pravoúhlé nekonečně hluboké potenciálové jámě o šířce \(L\) jsou stacionární stavy \[ \varphi_n= \begin{cases} \sqrt{\frac{2}{L}}\sin{\left(\frac{\pi nx}{L}\right)} & \quad \text{pro } x\in (0,L),\\ 0 & \quad \text{jinak,}\\ \end{cases}\] a energie \[E_n=\frac{\pi^2 \hbar^2}{2mL^2}n^2,\] kde \(n = 1{,}2,3,\dots\)

  Libovolnou vlnovou funkci \(\psi\) popisující přípustný stav částice, lze zapsat jako lineární kombinaci stacionárních stavů \(\varphi_n\) \[\psi=\sum_{n}{c_n\varphi_n},\] kde koeficienty \(c_n\) spočítáme jako „průmět“ obecné funkce na stacionární funkci, tj. pomocí skalárního součinu \(c_n=<\varphi_n| \psi>\).

  Pravděpodobnost \(p_n\) naměření konkrétní energie \(E_n\) ve stavu popsaném vlnovou funkcí \(\psi\) získáme pomocí koeficientů \(c_n\) jako

  \[p_n=|c_n|^2.\]

• Nápověda d)

  Střední hodnota operátoru \(\hat O\) ve stavu popsaném normovanou vlnovou funkcí \(\psi\) se vypočítá pomocí skalárního součinu

  \[\langle \hat O\rangle _\psi=<\psi| \hat O\psi>.\]

  Zamyslete se, jaký operátor je přiřazen celkové energii.

  Pokuste se napsat, jak bychom mohli vypočítat střední hodnotu energie pomocí naměřitelných energií a jejich pravděpodobností.

• Řešení nápovědy d)

  Operátor celkové energie obvykle nazýváme hamiltonián. Střední hodnotu energie ve stavu popsaném normovanou vlnovou funkcí \(\psi\) tedy vypočítáme

  \[\langle E_n\rangle_\psi =<\psi| \hat H\psi>.\]

  Střední hodnotu energie lze také vyjádřit jako vážený průměr naměřitelných energií \(E_n\), kde váhami jsou pravděpodobnosti naměření těchto energií

  \[\langle E_n\rangle_\psi =\sum_n p_nE_n=\sum_n |c_n|^2E_n.\]

  Uvědomte si, že pro normovanou vlnovou funkci platí \(\sum_n|c_n|^2=1\), a proto má vážený průměr tento zjednodušený tvar.

• Nápověda e)

  Vyhledejte, v jakém tvaru se zapisuje vlnová funkce včetně časové části.

• Řešení nápovědy e)

  Z řešení Schrödingerovy rovnice plyne, že stacionární vlnová funkce má separovaný tvar, tj. lze ji napsat jako součin prostorové části \(\varphi_n(x)\) a časové části \(T_n(t)\) \[\varphi_n(x,t)=\varphi_n(x)T_n(t)\] a časová část má tvar \[T_n(t)=\,\mathrm{e}^{-i\frac{E_n}{\hbar}t},\] kde \(E_n\) jsou hodnoty energie systému.

  Pokud máme zadanou prostorovou část nějaké obecné vlnové funkce \(\psi(x)\), tak ji můžeme chápat jako vlnovou funkci v čase \(t=0\). Tuto vlnovou funkci napíšeme jako lineární kombinaci stacionárních vlnových funkcí \[\psi(x,t=0)=\sum_{n} c_n\varphi_n(x, t=0).\] Potom nahradíme stacionární vlnové funkce \(\varphi_n(x, t=0)=\varphi_n(x)\) funkcemi v obecném čase \(\varphi_n(x, t)\), tj. přidáme uvedený časový člen \[\psi(x,t)=\sum_{n}{c_n\varphi_n(x)\,\mathrm{e}^{-i\frac{E_n}{\hbar}t}}.\]

• Řešení

  Zkoumáme částici v jednorozměrné pravoúhlé nekonečně hluboké potenciálové jámě o šířce \(L\), která se v čase \(t=0 \mathrm{s}\) nachází ve stavu popsaném vlnovou funkcí

  \[ \psi(x,t=0 \mathrm{s})= \begin{cases} N\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right] & \quad \text{pro } x\in (0,L),\\ 0 & \quad \text{jinak.}\\ \end{cases}\]

   

  a) Normovat vlnovou funkci \(\psi\) znamená určit hodnotu normalizační konstanty \(N\). Do normovací podmínky

  \[1=<\psi| \psi>=\int_{-\infty}^\infty{\psi^\ast\psi}\,\mathrm{d}x=\]

  dosadíme zadanou funkci \(\psi\) na intervalu \((0, L)\), neboť jinde je \(\psi\) nulová.

  \[=\int_0^L{N^\ast\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]N\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x=\]

  Vytkneme normalizační konstantu před integrál a dosadíme hodnotu integrálu (viz oddíl Výpočet integrálů níže).

  \[=|N|^2\int_0^L{\sin^2{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]^2}\,\mathrm{d}x=|N|^2L\]

  Z rovnice \(1=|N|^2L\) vyjádříme velikost normalizační konstanty \[\left |N\right\vert=\frac{1}{\sqrt{L}}.\]

  Normovaná vlnová funkce má tvar \[ \psi(x, t=0 \mathrm{s})= \begin{cases} \frac{1}{\sqrt{L}}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right] & \quad \text{pro } x\in (0,L),\\ 0 & \quad \text{jinak.}\\ \end{cases}\]

   

  b) Stacionární stavy jsou stavy kvantového systému popsané vlnovými funkcemi \(\varphi_n(x)\), které jsou řešením stacionární Schrödingerovy rovnice \[\hat{H}\varphi_n(x)=E_n\varphi_n(x)\] a mají pro jednorozměrnou pravoúhlou nekonečně hlubokou potenciálovou jámu o šířce \(L\) normovaný tvar \[ \varphi_n= \begin{cases} \sqrt{\frac{2}{L}}\sin{\left(\frac{\pi nx}{L}\right)} & \quad \text{pro } x\in (0,L),\\ 0 & \quad \text{jinak.}\\ \end{cases}\] Zadaný stav částice, popsaný vlnovou funkcí \(\psi(x)\), musí být lineární kombinací stacionárních stavů \(\varphi_n(x)\) \[\psi(x)=\sum_n{c_n\varphi_n(x)},\] kde \(c_n\) jsou koeficienty, pro které platí \[c_n=<\varphi_n| \psi>.\]

  Vypočítáme koeficienty \(c_n\) pro zadaný stav \(\psi(x)\) na intervalu \((0, L)\), protože mimo tento interval je \(\psi(x)\) nulová. Dosadíme normované funkce \(\varphi_n(x), \psi(x)\) a upravíme.

  \[c_n=<\varphi_n| \psi>=\int_{0}^L{\varphi_n^\ast\psi}\,\mathrm{d}x=\int_{0}^L{\sqrt{\frac{2}{L}}\sin{\left(\frac{\pi nx}{L}\right)}\frac{1}{\sqrt{L}}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x=\] \[=\frac{\sqrt{2}}{L}\int_{0}^L{\sin{\left(\frac{\pi nx}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x\]

  Po dosazení hodnoty integrálu (viz Výpočet integrálů) získáme koeficienty

  \[c_n=\frac{\sqrt{2}}{L}\cdot 0=0\quad \text{pro }n\geq 3,\] \[c_1=c_2=\frac{\sqrt{2}}{L}\frac{L}{2}=\frac{\sqrt{2}}{2}.\]

  Zadaný stav \(\psi(x)\) rozložíme na stacionární stavy \(\varphi_n(x)\)

  \[\psi(x)=\sum_n{c_n\varphi_n(x)}=c_1\varphi_1(x)+c_2\varphi_2(x)=\frac{\sqrt{2}}{2}\varphi_1(x)+\frac{\sqrt{2}}{2}\varphi_2(x)=\] \[=\frac{\sqrt{2}}{2}\left[\sqrt{\frac{2}{L}}\sin{\left(\frac{\pi x}{L}\right)}+\sqrt{\frac{2}{L}}\sin{\left(\frac{2\pi x}{L}\right)}\right].\]

  Poznámka: Zadaný stav \(\psi(x)\) můžeme velmi jednoduše rozložit na stacionární stavy \(\varphi_n(x)=\sqrt{\frac{2}{L}}\sin{\left(\frac{\pi nx}{L}\right)}\), aniž bychom počítali integrály. Stačí upravit normovaný stav \(\psi(x)\) pomocí vztahu \(\sin 2\alpha=2\sin\alpha\cos\alpha\).

  \[\psi(x)=\frac{1}{\sqrt{L}}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]=\frac{1}{\sqrt{L}}\left[\sin{\left(\frac{\pi x}{L}\right)}+2\sin{\left(\frac{\pi x}{L}\right)}\cos{\left(\frac{\pi x}{L}\right)}\right]=\] \[=\frac{1}{\sqrt{L}}\left[\sin{\left(\frac{\pi x}{L}\right)}+\sin{\left(\frac{2\pi x}{L}\right)}\right]=\frac{\sqrt{2}}{2}\left[\sqrt{\frac{2}{L}}\sin{\left(\frac{\pi x}{L}\right)}+\sqrt{\frac{2}{L}}\sin{\left(\frac{2\pi x}{L}\right)}\right]=\frac{\sqrt{2}}{2}\left[\varphi_1(x)+\varphi_2(x)\right]\]

  Odtud hned určíme koeficienty \(c_1=c_2=\frac{\sqrt{2}}{2}\).

   

  c) Řešením stacionární Schrödingerovy rovnice \[\hat{H}\varphi_n(x)=E_n\varphi_n(x)\] pro jednorozměrnou pravoúhlou nekonečně hlubokou potenciálovou jámu o šířce \(L\) jsou stacionární stavy \[ \varphi_n= \begin{cases} \sqrt{\frac{2}{L}}\sin{\left(\frac{\pi nx}{L}\right)} & \quad \text{pro } x\in (0,L),\\ 0 & \quad \text{jinak}\\ \end{cases}\] a energie \[E_n=\frac{\pi^2 \hbar^2}{2mL^2}n^2.\]

  V libovolném stavu můžeme naměřit jen energie odpovídající vlastním číslům \(E_n\) operátoru \(\hat H\), pro které má Schrödingerova rovnice netriviální řešení \(\varphi_n(x)\).

  Zadaný stav popsaný vlnovou funkcí \(\psi(x)\) je složen ze stacionárních stavů \(\varphi_1(x)\) a \(\varphi_2(x)\), můžeme v něm tedy naměřit jen energie \[E_1=\frac{\pi^2 \hbar^2}{2mL^2},\] \[E_2=\frac{2\pi^2 \hbar^2}{mL^2}=4E_1.\]

  Pravděpodobnost \(p_n\), že ve stavu popsaném vlnovou funkcí \(\psi(x)=\sum_n{c_n\varphi_n(x)}\) naměříme energii \(E_n\) je dána vztahem \[p_n=|c_n|^2.\]

  Po dosazení koeficientů \(c_1=c_2=\frac{\sqrt{2}}{2}\) vypočítáme pravděpodobnost naměření energie \(E_1\) a energie \(E_2\) v zadaném stavu \(\psi(x)\) \[p_1=p_2=|c_1|^2=|c_2|^2=\left(\frac{\sqrt{2}}{2}\right)^2=\frac{1}{2}.\] Naměření energie \(E_1=\frac{\pi^2 \hbar^2}{2mL^2}\) a energie \(E_2=4E_1=\frac{2\pi^2 \hbar^2}{mL^2}\) je stejně pravděpodobné, a to \(\frac{1}{2}\).

   

  d) Střední hodnota energie ve stavu popsaném normovanou vlnovou funkcí \(\psi(x)\) se vypočítá pomocí skalárního součinu, což lze upravit na vážený průměr naměřitelných energií \(E_n\), kde váhami jsou pravděpodobnosti \(p_n\) naměření jednotlivých hodnot

  \[\left\langle E\right\rangle_\psi=<\psi|\hat{H}\psi>=\sum_{n}{p_n E_n}=\sum_{n}{\left |c_n\right\vert^2 E_n}.\]

  Po dosazení koeficientů \(c_1=c_2=\frac{\sqrt{2}}{2}\) a energií \(E_1=\frac{\pi^2 \hbar^2}{2mL^2},\: E_2=4E_1=\frac{2\pi^2 \hbar^2}{mL^2}\) dostáváme střední hodnotu energie pro zadaný stav popsaný vlnovou funkcí \(\psi(x)\) \[\left\langle E\right\rangle_\psi=\sum_n{\left |c_n\right\vert^2 E_n}=|c_1|^2E_1+|c_2|^2E_2=\frac{1}{2}\left(E_1+4E_1\right)=\frac{1}{2}\cdot\frac{5\pi^2 \hbar^2}{2mL^2}=\frac{5\pi^2 \hbar^2}{4mL^2}.\]

   

  e) Časový vývoj obecného stavu \(\psi(x)\) popisuje vlnová funkce ve tvaru \[\psi(x, t)=\sum_{n}{c_n\varphi_n(x)\,\mathrm{e}^{-i\frac{E_n}{\hbar}t}},\] kde členy \(\,\mathrm{e}^{-i\frac{E_n}{\hbar}t}\) představují časovou část jednotlivých vlastních funkcí \(\varphi_n(x)\).

  Dosazením koeficientů \(c_1=c_2=\frac{\sqrt{2}}{2}\), vlastních funkcí \(\varphi_1(x)=\sqrt{\frac{2}{L}}\sin{\left(\frac{\pi x}{L}\right)}\), \(\varphi_2(x)=\sqrt{\frac{2}{L}}\sin{\left(\frac{2\pi x}{L}\right)}\) a energií \(E_1\), \(E_2=4E_1\) získáme zadanou vlnovou funkci \(\psi(x, 0)\) v obecném čase \(t\)

  \[\psi(x, t)=\sum_{n}{c_n\varphi_n(x)\,\mathrm{e}^{-i\frac{E_n}{\hbar}t}}= c_1\varphi_1(x)\,\mathrm{e}^{-i\frac{E_1}{\hbar}t}+c_2\varphi_2(x)\,\mathrm{e}^{-i\frac{E_2}{\hbar}t}=\] \[=\frac{\sqrt{2}}{2}\left[\varphi_1(x)\,\mathrm{e}^{-i\frac{E_1}{\hbar}t}+\varphi_2(x)\,\mathrm{e}^{-i\frac{4E_1}{\hbar}t}\right] =\frac{1}{\sqrt{L}}\left[\sin{\left(\frac{\pi x}{L}\right)}\,\mathrm{e}^{-i\frac{E_1}{\hbar}t}+\sin{\left(\frac{2\pi x}{L}\right)}\,\mathrm{e}^{-i\frac{4E_1}{\hbar}t}\right].\]

   

  Vlnovou funkci v čase \(t=\frac{\pi\hbar}{E_1}\) určíme dosazením tohoto času do vlnové funkce v obecném čase \(t\) \[\psi\left(x, t=\frac{\pi\hbar}{E_1}\right)= \frac{1}{\sqrt{L}}\left[\sin{\left(\frac{\pi x}{L}\right)}\,\mathrm{e}^{-i\frac{E_1}{\hbar}\frac{\pi\hbar}{E_1}}+\sin{\left(\frac{2\pi x}{L}\right)}\,\mathrm{e}^{-i\frac{4E_1}{\hbar}\frac{\pi\hbar}{E_1}}\right]=\] \[=\frac{1}{\sqrt{L}}\left[\sin{\left(\frac{\pi x}{L}\right)}\,\mathrm{e}^{-i\pi}+\sin{\left(\frac{2\pi x}{L}\right)}\,\mathrm{e}^{-i4\pi}\right]=\] a upravením pomocí vztahu \(\,\mathrm{e}^{iz}=\cos z +i\sin z\)

  \[=\frac{1}{\sqrt{L}}\left[\sin{\left(\frac{\pi x}{L}\right)}(\cos{(-\pi)}+i\sin{(-\pi)})+\sin{\left(\frac{2\pi x}{L}\right)}(\cos{(-4\pi)}+i\sin{(-4\pi)})\right]=\] \[=\frac{1}{\sqrt{L}}\left[-\sin{\left(\frac{\pi x}{L}\right)}+\sin{\left(\frac{2\pi x}{L}\right)}\right]=\frac{\sqrt{2}}{2}\left[-\varphi_1(x)+\varphi_2(x)\right].\]

• Výpočet integrálů

  Postup při výpočtu integrálů bude stejný. Nejdříve upravíme funkci, kterou chceme integrovat, roznásobením a využitím vztahů pro goniometrické funkce \[\sin{2\alpha}=2\sin{\alpha}\cos{\alpha},\] \[\sin^2{\alpha}=\frac{1-\cos{2\alpha}}{2},\] \[\sin{\alpha}\,\sin{\beta}=\frac{\cos{(\alpha -\beta)}-\cos{(\alpha +\beta)}}{2},\] pak ji zintegrujeme pomocí základních integrálů \[\int{a}\,\mathrm{d}x=ax+c,\] \[\int{a\cos{bx}}\,\mathrm{d}x=a\frac{\sin{bx}}{b}+c,\] kde \(a,\, b\) jsou konstanty \((b\neq 0)\) a \(c\) je integrační konstanta. Nakonec vypočteme hodnotu integrálu dosazením integračních mezí.

   

  Výpočet normalizační konstanty

  Nyní vypočteme integrál potřebný při normování vlnové funkce,

  \[\int_0^L{\sin^2{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]^2}\,\mathrm{d}x=\]

  funkci umocníme a roznásobíme,

  \[=\int_0^L{\left[\sin^2{\left(\frac{\pi x}{L}\right)}+4\sin^2{\left(\frac{\pi x}{L}\right)}\cos{\left(\frac{\pi x}{L}\right)}+4\sin^2{\left(\frac{\pi x}{L}\right)}\cos^2{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x=\]

  použijeme vztah \(\sin{2\alpha}=2\sin{\alpha}\cos{\alpha}\),

  \[=\int_0^L{\left[\sin^2{\left(\frac{\pi x}{L}\right)}+2\sin{\left(\frac{2\pi x}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}+\sin^2{\left(\frac{2\pi x}{L}\right)}\right]}\,\mathrm{d}x=\]

  použijeme vztahy \(\sin^2{\alpha}=\frac{1-\cos{2\alpha}}{2}\) a \(\sin{\alpha}\,\sin{\beta}=\frac{\cos{(\alpha -\beta)}-\cos{(\alpha +\beta)}}{2}\),

  \[=\int_0^L{\left[\frac{1-\cos{\left(\frac{2\pi x}{L}\right)}}{2}+\cos{\left(\frac{\pi x}{L}\right)}-\cos{\left(\frac{3\pi x}{L}\right)}+\frac{1-\cos{\left(\frac{4\pi x}{L}\right)}}{2}\right]}\,\mathrm{d}x=\]

  upravíme, zintegrujeme pomocí základních integrálů a určíme hodnotu integrálu.

  \[=\int_0^L{\left[1+\cos{\left(\frac{\pi x}{L}\right)}-\frac{1}{2}\cos{\left(\frac{2\pi x}{L}\right)}-\cos{\left(\frac{3\pi x}{L}\right)}-\frac{1}{2}\cos{\left(\frac{4\pi x}{L}\right)}\right]}\,\mathrm{d}x=\] \[=\left[x+\frac{\sin{\left(\frac{\pi x}{L}\right)}}{\frac{\pi }{L}}-\frac{1}{2}\frac{\sin{\left(\frac{2\pi x}{L}\right)}}{\frac{2\pi }{L}}-\frac{\sin{\left(\frac{3\pi x}{L}\right)}}{\frac{3\pi }{L}}-\frac{1}{2}\frac{\sin{\left(\frac{4\pi x}{L}\right)}}{\frac{4\pi x}{L}}\right]_0^L=L\]

   

  Výpočet koeficientů \(c_n\)

  Zde vypočteme hodnotu integrálu, který se vyskytuje při určování koeficientů \(c_n\),

  \[I_n=\int_0^L{\sin{\left(\frac{\pi nx}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x=\]

  funkci roznásobíme a použijeme vztah \(\sin{2\alpha}=2\sin{\alpha}\cos{\alpha}\),

  \[=\int_0^L{\left[\sin{\left(\frac{\pi nx}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}+\sin{\left(\frac{\pi nx}{L}\right)}\sin{\left(\frac{2\pi x}{L}\right)}\right]}\,\mathrm{d}x=\]

  použijeme vztah \(\sin{\alpha}\,\sin{\beta}=\frac{\cos{(\alpha -\beta)}-\cos{(\alpha +\beta)}}{2}\),

  \[=\int_0^L{\left[\frac{\cos{\left(\frac{\pi (n-1)x}{L}\right)}-\cos{\left(\frac{\pi (n+1)x}{L}\right)}}{2}+\frac{\cos{\left(\frac{\pi (n-2)x}{L}\right)}-\cos{\left(\frac{\pi (n+2)x}{L}\right)}}{2}\right]}\,\mathrm{d}x=\]

  vytkneme konstantu před integrál a funkci upravíme.

  \[=\frac{1}{2}\int_0^L{\left[\cos{\left(\frac{\pi (n-2)x}{L}\right)}+\cos{\left(\frac{\pi (n-1)x}{L}\right)}-\cos{\left(\frac{\pi (n+1)x}{L}\right)}-\cos{\left(\frac{\pi (n+2)x}{L}\right)}\right]}\,\mathrm{d}x\]

  Je-li \(n\geq 3\) můžeme integrovat a vypočítat hodnotu integrálu

  \[I_3=\frac{1}{2}\left[\frac{\sin{\left(\frac{\pi (n-2)x}{L}\right)}}{\frac{\pi (n-2)}{L}}+\frac{\sin{\left(\frac{\pi (n-1)x}{L}\right)}}{\frac{\pi (n-1)}{L}}-\frac{\sin{\left(\frac{\pi (n+1)x}{L}\right)}}{\frac{\pi (n+1)}{L}}-\frac{\sin{\left(\frac{\pi (n+2)x}{L}\right)}}{\frac{\pi (n+2)}{L}}\right]_0^L=\frac{1}{2}\cdot 0=0.\]

  Pro \(n=2\) dosadíme za \(n\) a spočítáme integrál

  \[I_2=\frac{1}{2}\int_0^L{\left[1+\cos{\left(\frac{\pi x}{L}\right)}-\cos{\left(\frac{3\pi x}{L}\right)}-\cos{\left(\frac{4\pi x}{L}\right)}\right]}\,\mathrm{d}x=\] \[=\frac{1}{2}\left[x+\frac{\sin{\left(\frac{\pi x}{L}\right)}}{\frac{\pi}{L}}-\frac{\sin{\left(\frac{3\pi x}{L}\right)}}{\frac{3\pi }{L}}-\frac{\sin{\left(\frac{4\pi x}{L}\right)}}{\frac{4\pi }{L}}\right]_0^L=\frac{1}{2}L=\frac{L}{2}.\]

  Pro \(n=1\) počítáme hodnotu integrálu

  \[I_1=\frac{1}{2}\int_0^L{\left[\cos{\left(\frac{-\pi x}{L}\right)}+1-\cos{\left(\frac{2\pi x}{L}\right)}-\cos{\left(\frac{3\pi x}{L}\right)}\right]}\,\mathrm{d}x=\] \[=\frac{1}{2}\left[\frac{\sin{\left(\frac{-\pi x}{L}\right)}}{\frac{-\pi}{L}}+x-\frac{\sin{\left(\frac{2\pi x}{L}\right)}}{\frac{2\pi }{L}}-\frac{\sin{\left(\frac{3\pi x}{L}\right)}}{\frac{3\pi }{L}}\right]_0^L=\frac{1}{2}L=\frac{L}{2}.\]

   

  Na závěr uvedeme postup při výpočtu integrálů v rozhraní WolframAlpha.

  Výpočet normalizační konstanty

  Do řádku pro výpočet se zapíše integrál \(\int_0^L{\sin^2{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]^2}\,\mathrm{d}x\) ve tvaru

  integrate sin^2 (pi*x/L) * (1+2*cos (pi*x/L))^2 dx from x=0 to L,

  klikne se na tlačítko = (compute) a zobrazí se vypočtená hodnota integrálu

  \[\int_0^L{\sin^2{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]^2}\,\mathrm{d}x=L.\]

   

  Výpočet koeficientů \(c_n\)

  Intergrál \(\int_0^L{\sin{\left(\frac{\pi nx}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x\) se zapíše ve tvaru

  integrate sin (pi*n*x/L)* sin (pi*x/L)* (1+2*cos (pi*x/L)) dx from x=0 to L,

  po výpočtu a úpravě je hodnota integrálu pro \(n\geq 3\)

  \[\int_0^L{\sin{\left(\frac{\pi nx}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x=\frac{L(n^2+2)\sin(\pi n)}{\pi (n^2-4)(n^2-1)}=0.\]

  Pro \(n=2\) je třeba spočítat integrál \(\int_0^L{\sin{\left(\frac{2\pi x}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x\), který se zadá ve tvaru

  integrate sin (2*pi*x/L)* sin (pi*x/L)* (1+2*cos (pi*x/L)) dx from x=0 to L,

  po výpočtu je hodnota integrálu

  \[\int_0^L{\sin{\left(\frac{2\pi x}{L}\right)}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x=\frac{L}{2}.\]

  Pro \(n=1\) se počítá integrál \(\int_0^L{\sin^2{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x\), který se napíše ve tvaru

  integrate sin^2 (pi*x/L)* (1+2*cos (pi*x/L)) dx from x=0 to L,

  po výpočtu je hodnota integrálu

  \[\int_0^L{\sin^2{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right]}\,\mathrm{d}x=\frac{L}{2}.\]

• Odpověď

  a) Normovaná vlnová funkce má pro \(x\in (0,L)\) tvar \[\psi(x, t=0 \mathrm s)=\frac{1}{\sqrt{L}}\sin{\left(\frac{\pi x}{L}\right)}\left[1+2\cos{\left(\frac{\pi x}{L}\right)}\right].\]

  b) Stav popsaný vlnovou funkcí \(\psi(x)\) lze rozložit na stacionární stavy \(\varphi_n(x)\)

  \[\psi(x)=\frac{\sqrt{2}}{2}\varphi_1(x)+\frac{\sqrt{2}}{2}\varphi_2(x)=\frac{\sqrt{2}}{2}\left[\sqrt{\frac{2}{L}}\sin{\left(\frac{\pi x}{L}\right)}+\sqrt{\frac{2}{L}}\sin{\left(\frac{2\pi x}{L}\right)}\right].\]

  c) Ve stavu popsaném vlnovou funkcí \(\psi(x)\) je možné naměřit jen energie \[E_1=\frac{\pi^2 \hbar^2}{2mL^2},\] \[E_2=4E_1=\frac{2\pi^2 \hbar^2}{mL^2},\] obě se stejnou pravděpodobností \(\frac{1}{2}\).

  d) Střední hodnota energie ve stavu popsaném vlnovou funkcí \(\psi(x)\) je \[\left\langle E\right\rangle_\psi=\frac{5\pi^2 \hbar^2}{4mL^2}.\]

  e) Vlnová funkce v obecném čase \(t\) se vyjádří \[\psi(x, t)=\frac{\sqrt{2}}{2}\left[\varphi_1(x)\,\mathrm{e}^{-i\frac{E_1}{\hbar}t}+\varphi_2(x)\,\mathrm{e}^{-i\frac{4E_1}{\hbar}t}\right] =\frac{1}{\sqrt{L}}\left[\sin{\left(\frac{\pi x}{L}\right)}\,\mathrm{e}^{-i\frac{E_1}{\hbar}t}+\sin{\left(\frac{2\pi x}{L}\right)}\,\mathrm{e}^{-i\frac{4E_1}{\hbar}t}\right].\]

  Vlnová funkce v čase \(t=\frac{\pi\hbar}{E_1}\) má tvar \[\psi\left(x, t=\frac{\pi\hbar}{E_1}\right)=\frac{\sqrt{2}}{2}\left[-\varphi_1(x)+\varphi_2(x)\right]=\frac{1}{\sqrt{L}}\left[-\sin{\left(\frac{\pi x}{L}\right)}+\sin{\left(\frac{2\pi x}{L}\right)}\right].\]