Sbírka řešených úloh

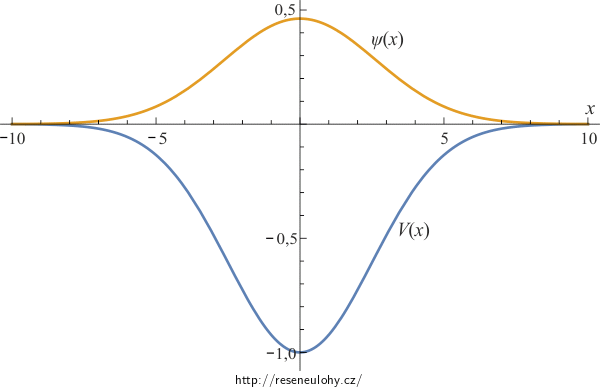
Potenciál tvaru Gaussovy křivky

Úloha číslo: 2237

• Nápověda 1

  Připomeňte si princip variační metody.

• Řešení nápovědy 1

  Variační metoda je jednou z přibližných metod kvantové mechaniky. Používá se pro výpočet energie a zjištění vlnových funkcí základního stavu a nižších excitovaných stavů systémů, jejichž hamiltonián nezávisí na čase.

  Sestavíme-li funkcionál \(\mathbb{F}\), definovaný na prostoru přípustných vlnových funkcí \(\boldsymbol{H}\) \[\mathbb{F}(\psi)=\frac{\langle\psi|\hat{H}\psi\rangle}{\langle\psi|\psi\rangle},\] který každé funkci \(\psi\) přiřadí střední hodnotu energie ve stavu popsaném danou vlnovou funkcí, dojdeme úvahou k závěru, že základní stav má nejnižší hodnotu střední energie a tedy hledáme minimum tohoto funkcionálu.

  Pokud bychom hledali minimum na celém prostoru \(\boldsymbol{H}\), dostali bychom přesné řešení. Tento postup by byl srovnatelně obtížný s řešením Schrödingerovy rovnice. Pokud je toto příliš náročné, zvolíme vhodnou podmnožinu prostoru \(\boldsymbol{H}\), na které provádíme minimalizaci. Nalezené minimum energie na zvolené podmnožině bude v mnoha případech vyšší než skutečné minimum energie základního stavu, takže nám dává horní odhad energie základního stavu. Pouze v případě, že by námi zvolená podmnožina \(\boldsymbol{H}\) obsahovala i přesné řešení, se budou hodnoty rovnat.

  Postup je tedy takový, že nejprve stanovíme tvar vlnových funkcí \(\psi(x;\alpha_i)\), kde \(\alpha_i\) jsou parametry, na kterých provedeme minimalizaci. Funkce \(\psi(x;\alpha_i)\) poté dosadíme do funkcionálu střední hodnoty energie a jeho minimum budeme hledat.

• Nápověda 2

  Sestavme funkcionál

  \[\mathbb{F}(\psi)=\frac{\langle\psi|\hat{H}\psi\rangle}{\langle\psi|\psi\rangle}=\frac{\langle\psi|(\hat{T}+\hat{V})\psi\rangle}{\langle\psi|\psi\rangle}=\frac{\langle\psi|(−\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d} x^2}+V)\psi\rangle}{\langle\psi|\psi\rangle}.\]

  Připomeňte si hledání jeho minima.

• Řešení nápovědy 2

  Po dosazení vlnové funkce \(\psi(x;\alpha)\) do funkcionálu \(\mathbb{F}(\psi)=\frac{\langle\psi|\hat{H}\psi\rangle}{\langle\psi|\psi\rangle}=E(\alpha)\) dostaneme funkci jedné proměnné \(\alpha\). Nyní hledáme minimum funkce jedné proměnné, tedy taková \(\alpha\), pro která je první derivace \(\frac{\mathrm{d}E(\alpha) }{\mathrm{d} x}\) nulová a zároveň druhá derivace \(\frac{\mathrm{d}^2E(\alpha) }{\mathrm{d} x^2}\) kladná.

• Nápověda 3 – Poissonovy integrály

  Při řešení úlohy využijeme známých hodnot Poissonových integrálů \[\int_{−\infty}^\infty{e^{−ax^2}}\,\mathrm{d}x=\sqrt{\frac{\pi}{a}},\] \[\int_{−\infty}^\infty{x^2e^{−ax^2}}\,\mathrm{d}x=\frac{1}{2}\sqrt{\frac{\pi}{a^{3}}}.\]

• Řešení

  Hledáme minimální střední energii systému a vlnovou funkci, která popisuje stav s touto energií. Sestavme proto nyní funkcionál, jehož minimum budeme hledat

  \[\mathbb{F}(\psi)=\frac{\langle\psi|\hat{H}\psi\rangle}{\langle\psi|\psi\rangle}=\frac{\langle\psi|(\hat{T}+\hat{V})\psi\rangle}{\langle\psi|\psi\rangle}.\]

  Dosaďme teď do funkcionálu předpis funkcí, na kterých budeme hledat jeho minimum.

  Nejprve určíme hodnotu skalárního součinu ve jmenovateli funkcionálu

  \[\langle\psi|\psi\rangle=\int_{−\infty}^\infty{\sqrt{\frac{2\alpha}{\pi}}e^{−2ax^2}}\,\mathrm{d}x=\sqrt{\frac{2\alpha}{\pi}}\sqrt{\frac{\pi}{2\alpha}}=1.\]

  Zde vidíme, že naše vlnové funkce jsou normované. Při výpočtu jsme využili známé hodnoty Poissonových integrálů (viz nápověda výše).

  Dále si pro přehlednost výpočtu rozepíšeme Hamiltonův operátor \(\hat{H}\) do konkrétního tvaru \[\hat{H}=\hat{T}+\hat{V}=−\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d} x^2}−V_{0}e^{2\beta x^2}.\]

  Nyní si vypočítáme střední hodnoty jednotlivých členů Hamiltoniánu ve stavu popsaném vlnovou funkcí \(\psi(x;\alpha)\). Nejprve vypočteme výraz pro střední hodnotu potenciální energie

  \[\langle\psi|\hat{V}\psi\rangle=−\sqrt{\frac{2\alpha}{\pi}}V_{0}\int_{−\infty}^\infty{e^{−2(\alpha+\beta)x^2}}\,\mathrm{d}x=−\sqrt{\frac{2\alpha}{\pi}}V_{0}\frac{\sqrt{\pi}}{\sqrt{2(\alpha+\beta)}}=\] \[=−V_{0}\sqrt{\frac{\alpha}{\alpha+\beta}}.\]

  Dále si vypočítáme druhé derivace \(\psi\) podle \(x\), které použijeme ve výpočtu střední hodnoty \(\hat{T}\)

  \[\frac{\mathrm{d}^2}{\mathrm{d} x^2}e^{−\alpha x^2}=\frac{\mathrm{d}}{\mathrm{d} x}(−2\alpha xe^{−\alpha x^2})=(−2\alpha+ 4\alpha^2x^2)e^{−\alpha x^2}.\]

  Nyní dosadíme do vztahu pro střední hodnotu kinetické energie a opět využijeme známé hodnoty Poissonových integrálů \[\langle\psi|\hat{T}\psi\rangle=−\frac{\hbar^2}{2m}\sqrt{\frac{2\alpha}{\pi}}\int_{−\infty}^\infty{(−2\alpha+ 4\alpha^2x^2)e^{−2\alpha x^2}}\,\mathrm{d}x=\] \[=−\frac{\hbar^2}{2m}\sqrt{\frac{2\alpha}{\pi}}\left(-2\alpha\sqrt{\frac{\pi}{2\alpha}}+4\alpha^2\frac{1}{2}\sqrt{\frac{\pi}{(2\alpha)^{3}}}\right)=\]

  \[=−\frac{\hbar^2}{2m}(-2\alpha+\alpha)=\frac{\hbar^2}{2m}\alpha.\]

  Dosaďme do funkcionálu

  \[\mathbb{F}(\psi)=\frac{\langle\psi|\hat{H}\psi\rangle}{\langle\psi|\psi\rangle}=\frac{\hbar^2}{2m}\alpha−V_{0}\sqrt{\frac{\alpha}{\alpha+\beta}}=E(\alpha).\]

  Zde vidíme, že se funkcionál \(\mathbb{F}(\psi)\) po dosazení vlnové funkce \(\psi(x;\alpha)\) změnil na funkci jedné proměnné. Abychom odhadli minimální energii našeho systému, musíme hledat minimum funkce \(E(\alpha)\), které může být v bodech s nulovou první parciální derivaci podle \(\alpha\)

  \[\frac{\partial E(\alpha)}{\partial \alpha}=\frac{\hbar^2}{2m}−V_{0}\frac{1}{2}\sqrt{\frac{\alpha+\beta}{\alpha}}\frac{(\alpha+\beta)-\alpha}{(\alpha+\beta)^2}=0.\]

  Při výpočtu jsme využili pravidlo pro derivaci složené funkce a derivaci podílu. Dále budeme získanou rovnici řešit

  \[\frac{\hbar^2}{2m}\frac{2}{V_0}=\frac{\beta}{\sqrt{\alpha(\alpha+\beta)^3}},\] \[\alpha(\alpha+\beta)^3=\left(\frac{mV_0\beta}{\hbar^2}\right)^2\]

  Kladné kořeny této rovnice jsou naše hledaná řešení. K získání jejich přesné hodnoty bychom museli řešit kvartickou rovnici, což je značně obtížný úkol, kořeny lze ale získat např. numerickými metodami. Před tím si rovnici ještě upravíme do tvaru

  \[\frac{\alpha}{\beta}\left(\frac{\alpha}{\beta}+1\right)^3=\left(\frac{mV_0}{\beta\hbar^2}\right)^2,\]

  protože \(\alpha\) a \(\beta\) mají stejný rozměr – m⁻² (exponent musí být bezrozměrný ve výrazu pro potenciální energii i ve vlnové funkci), můžeme označit \(\frac{\alpha}{\beta}=\xi\) a řešit číselnou rovnici

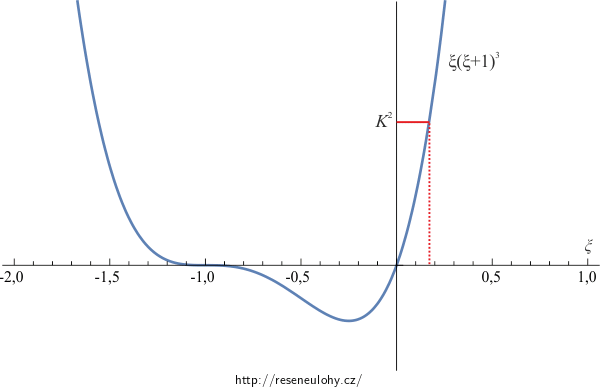
  \[\xi(\xi+1)^3=K^2,\]

  kde \(K\) je zlomek na pravé straně rovnice.

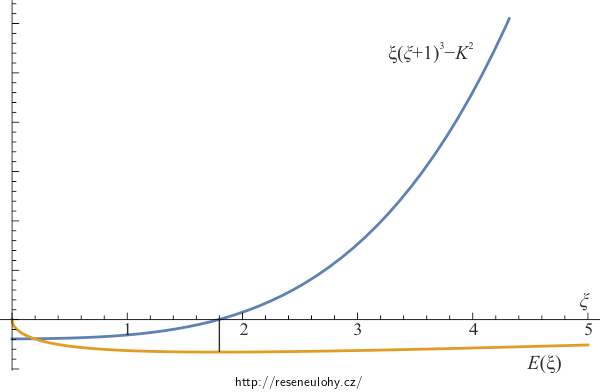
  Úvahou provedeme kontrolu, že díky tomu, že pravá strana rovnice je kladná, tak má vždy jedno kladné řešení. Levá strana je součinem výrazů \(\xi\) a \((\xi+1)^3\), což je součin prostých, rostoucích a pro kladné \(\xi\) i kladných funkcí. To znamená, že levá strana rovnice je pro kladná \(\xi\) rostoucí funkce, která procházející počátkem a zároveň pro \(\xi \rightarrow \infty\) roste nade všechny meze, tedy pro každou hodnotu pravé strany existuje \(\xi\) takové, že je rovnice splněna.

  Ještě názorněji je to vidět z grafu. Na obrázku je nakreslen graf funkce \(\xi(\xi+1)^3\). Vidíme, že pro libovolné \(K\) existuje kladné \(\xi\) takové, že bude řešit zadanou rovnici.

  

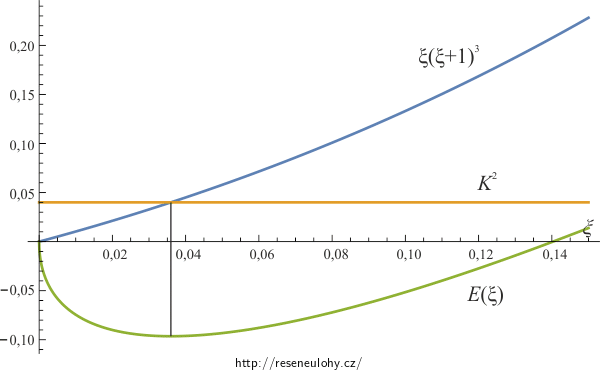
  Výraz pro střední hodnotu energie si také přepíšeme pomocí bezrozměrné proměnné \(\xi\):

  \[E(\alpha) = \frac{\hbar^2}{2m}\alpha−V_{0}\sqrt{\frac{\alpha}{\alpha+\beta}}=V_0\left(\frac{\xi}{2K}−\sqrt{\frac{\xi}{\xi+1}}\right)=E(\xi).\]

  A minimalizaci střední hodnoty energie můžeme zachytit graficky (v grafu pro hodnoty \(K=0{,}2).\)

  

• Odpověď

  Odhad energie základního stavu pro systém vázané částice na přímce s potenciální energií danou vztahem \(V(x)=−V_{0}e^{2\beta x^2}\) pomocí variační metody na třídě funkcí \(\psi=\sqrt[4]{\frac{2\alpha}{\pi}}e^{−\alpha x^2}\), kde \(V_{0}>0\), \(\beta>0\) a \(\alpha\) je kladný parametr, je dán rovnicí

  \[\langle E \rangle_\psi=\langle\psi|\hat{H}\psi\rangle=\frac{\hbar^2}{2m}\alpha−V_{0}\sqrt{\frac{\alpha}{\alpha+\beta}},\]

  kde \(\alpha\) je kladným kořenem rovnice

  \[\frac{\alpha}{\beta}\left(\frac{\alpha}{\beta}+1\right)^3=\left(\frac{mV_0}{\beta\hbar^2}\right)^2.\]

• Komentář – výpočet pro proton v jádře

  Zkusme jako konkrétní ilustraci dosadit hodnoty pro proton v jádře středně těžkého atomu a úlohu numericky dořešit. Typické hodnoty pro proton v jádře jsou:

  • hmotnost protonu \(m=1\,\mathrm{GeV/c}^2\),
  • velikost jádra je dána vztahem \(r=1{,}3\,\mathrm{fm} A^{\frac{1}{3}}\), kde \(A\) je hmotností číslo atomu, pro náš výpočet zvolme hodnotu \(r=5\,\mathrm{fm}\),
  • konstanta \(\beta\) udává šířku potenciálové jámy, položíme ji rovnu \(\frac{1}{r^2}\) a tedy \(\beta\approx\frac{1}{25}\,\mathrm{fm}^{-2}\),
  • \(V_0=10\,\mathrm{MeV}\),
  • \(\hbar c\,\dot{=}\, 200\,\mathrm{MeV\,fm}\).

  Tyto hodnoty nyní dosadíme do \(K\):

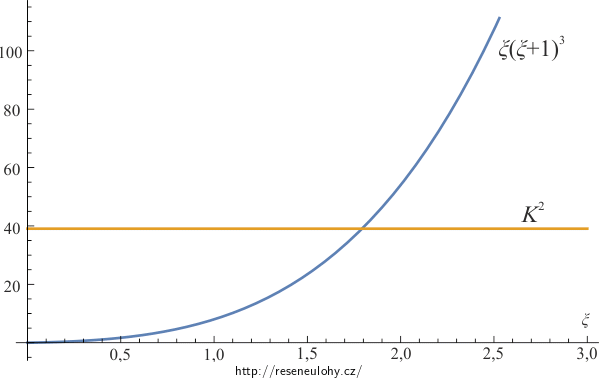
  \[K=\frac{mV_0}{\beta\hbar^2}=\frac{\frac{10^3\,\mathrm{MeV}}{c^2}·10\,\mathrm{MeV}}{{\frac{1}{25}\,\mathrm{fm}^{−2}\hbar^2 }}=\frac{10^3\,\mathrm{MeV}·10\,\mathrm{MeV}}{{(\frac{1}{25}\,\mathrm{fm}^{−2})(200\,\mathrm{MeV·fm})^2 }}=\frac{25}{4}.\]

  Poznámka: Z dosazení je vidět i to, že \(K\) je bezrozměrné.

  Numericky vyřešíme rovnici \[\xi\left(\xi+1\right)^3=K^2.\] Přibližná hodnota kladného kořene rovnice je \(\xi\doteq1{,}8.\) Tedy hledané \(\alpha\) je přibližně \(\alpha\doteq0{,}072\,\mathrm{fm}^{-2}\).

  

  Pomocí přepisu výrazu pro střední hodnotu energie pomocí bezrozměrné proměnné \(\xi\) \[E(\xi)=V_0\left(\frac{\xi}{2K}−\sqrt{\frac{\xi}{\xi+1}}\right)\] můžeme do jednoho grafu zachytit jak závislost střední hodnoty energie, tak rovnici pro hledání její nulové derivace. Z obrázku je patrné, že v okolí minima se energie příliš nemění se změnou parametru \(\alpha\).

  

  Dále můžeme dopočítat střední hodnotu energie odhadnutého základního stavu protonu v jádře dosazením do rovnice po střední hodnotu energie

  \[E(\alpha) = \langle E \rangle_\psi=\langle\psi|\hat{H}\psi\rangle=\frac{\hbar^2}{2m}\alpha−V_{0}\sqrt{\frac{\alpha}{\alpha+\beta}}=\frac{\hbar^2 c^2}{1\,\mathrm{GeV}}0{,}072\,\mathrm{fm}^{−2}−10\,\mathrm{MeV}\sqrt{\frac{0{,}072}{0{,}072+1}}=\] \[=\frac{(200\,\mathrm{MeV·fm})^2}{1\,\mathrm{GeV}}0{,}072\,\mathrm{fm}^{−2}−10\,\mathrm{MeV}·0{,}26\doteq0{,}3\,\mathrm{MeV}.\]