Nestacionární stav 1
Úloha číslo: 682
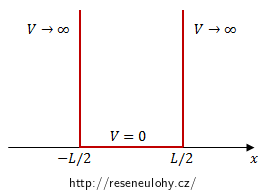
Částice se nachází v nekonečně hluboké potenciálové jámě šířky L:
V(x) = 0 pro |x| ≤ L/2 a V(x) → ∞ pro |x| > L/2.
Její stav v čase t = 0 popisuje normovaná vlnová funkce
\[\psi(x,\,t=0)=\sqrt{\frac{8}{5L}} \,\left[1\,+\, \sin\left(\frac{\pi x}{L}\right)\right]\,\cos\left(\frac{\pi x}{L}\right)\,.\]1) Napište předpis pro normovanou vlnovou funkci ψ(x, t) pro tuto částici včetně její časové závislosti.
2) Určete střední hodnotu energie částice v obecném čase t.
3) Určete pravděpodobnost, že se částice v čase t nachází
Nápověda 1
Jak vypadají normované vlastní funkce hamiltoniánu pro případ částice ve výše popsané nekonečně hluboké jednorozměrné potenciálové jámě? Jaké jim odpovídají energie? Jak vypadá časová závislost těchto stacionárních stavů?Nápověda 2
Vyjádřete funkci \[\psi(x,\,t=0)\] jako lineární kombinaci (superpozici) normovaných vlastních funkcí hamiltoniánu odpovídajícího dané situaci.
Řešení 1
Normované vlastní funkce hamiltoniánu pro případ částice ve výše popsané nekonečně hluboké pravoúhlé potenciálové jámě jsou
\(\hspace{40px}\psi_n(x)=\sqrt{\frac{2}{L}}\, \cos\left(\frac{n\pi x}{L}\right)\) pro n lichá a
\(\hspace{40px}\psi_n(x)=\sqrt{\frac{2}{L}}\, \sin\left(\frac{n\pi x}{L}\right)\) pro n sudá.
Jim odpovídají energie \[E_n=\frac{n^2 \pi^2 \hbar^2}{2mL^2}\,.\]
(Podrobné odvození najdete v úloze Symetrická nekonečná pravoúhlá jáma této sbírky.)
Z řešení časové části Schrödingerovy rovnice vyplývá závislost stacionárních stavů na čase přes faktor \(e^{-\frac{iE_n t}{\hbar}}\).
(Podrobnější vysvětlení najdete např. v knize SKÁLA, L. Úvod do kvantové mechaniky. Praha: Academia, 2005. ISBN 80-200-1316-4.)
Vlnovou funkci ψ(x, t = 0) zapíšeme jako lineární kombinaci prvních dvou stacionárních stavů částice v jámě. Platí
\[\psi(x,\,t=0)=\sqrt{\frac{8}{5L}} \,\left[1\,+\, \sin\left(\frac{\pi x}{L}\right)\right]\,\cos\left(\frac{\pi x}{L}\right)\,,\] \[\psi(x,\,t=0)=\sqrt{\frac{8}{5L}}\,\cos\left(\frac{\pi x}{L}\right) \,+\, \sqrt{\frac{8}{5L}}\,\sin\left(\frac{\pi x}{L}\right)\,\cos\left(\frac{\pi x}{L}\right),\] \[\psi(x,\,t=0)=\frac{2}{\sqrt{5}}\,\sqrt{\frac{2}{L}}\,\cos\left(\frac{\pi x}{L}\right)\,+\,\frac{1}{\sqrt{5}}\,\sqrt{\frac{2}{L}}\,\sin\left(\frac{2\pi x}{L}\right)\,,\] \[\psi(x,\,t=0)=\frac{2}{\sqrt{5}}\,\psi_1(x)\,+\,\frac{1}{\sqrt{5}}\,\psi_2(x)\,.\]Časová závislost nemá vliv na koeficienty této lineární kombinace. Je proto
\[\psi(x,\,t)=\frac{2}{\sqrt{5}}\,\psi_1(x)\,e^{-\frac{iE_1 t}{\hbar}}+\,\frac{1}{\sqrt{5}}\,\psi_2(x)\,e^{-\frac{iE_2 t}{\hbar}}\,,\] \[\psi(x,\,t)=\frac{2}{\sqrt{5}}\,\psi_1(x)\,e^{-\frac{iE_1 t}{\hbar}}+\,\frac{1}{\sqrt{5}}\,\psi_2(x)\,e^{-\frac{i4E_1 t}{\hbar}}\,,\] \[\psi(x,\,t)=\frac{2}{\sqrt{5}}\,\sqrt{\frac{2}{L}}\,\cos\left(\frac{\pi x}{L}\right)\,e^{-\frac{iE_1 t}{\hbar}}+\,\frac{1}{\sqrt{5}}\,\sqrt{\frac{2}{L}}\,\sin\left(\frac{2\pi x}{L}\right)\,e^{-\frac{i4E_1 t}{\hbar}}\,,\] \[\psi(x,\,t)=\sqrt{\frac{2}{5L}}\,\left[2\, \cos\left(\frac{\pi x}{L}\right)\,e^{-\frac{iE_1 t}{\hbar}}+\,\sin\left(\frac{2\pi x}{L}\right)\,e^{-\frac{i4E_1 t}{\hbar}}\right]\,,\]kde \(E_1=\frac{\pi^2 \hbar^2}{2mL^2}\).
Nápověda ke 2 – střední hodnota veličiny
Jak se v kvantové mechanice určují střední hodnoty fyzikálních veličin? Jak určíme střední hodnotu energie, je-li operátorem energie hamiltonián \(\hat{H}\)?
Řešení 2 – první verze (z definice)
Uvědomíme-li si, že operátorem energie je tzv. Hamiltonův operátor, potom střední hodnotu energie \(\langle E(t) \rangle\) v čase t spočteme z definice jako
\[ \langle E(t) \rangle = \langle \hat{H} \rangle = \int_{-\frac{L}{2}}^{\frac{L}{2}} \psi*(x,\,t) \,\hat{H}\psi(x,\,t) \,\mbox{d}x\,, \] \[ \langle E(t) \rangle = \] \[=\int_{-\frac{L}{2}}^{\frac{L}{2}} \sqrt{\frac{2}{5L}}\,\left[2\, \cos\left(\frac{\pi x}{L}\right)\,e^{\frac{iE_1 t}{\hbar}}+\,\sin\left(\frac{2\pi x}{L}\right)\,e^{\frac{iE_2 t}{\hbar}}\right]\,\cdot\,\hat{H}\,\sqrt{\frac{2}{5L}}\,\left[2\, \cos\left(\frac{\pi x}{L}\right)\,e^{-\frac{iE_1 t}{\hbar}}+\,\sin\left(\frac{2\pi x}{L}\right)\,e^{-\frac{iE_2 t}{\hbar}}\right]\,\mbox{d}x\,. \]Uvědomme si, že pro vlastní funkce hamiltoniánu platí \(\hat{H}\psi_n(x,\,t)=E_n\psi_n(x,\,t)\,.\)Po roznásobení se navíc uprostřed výše uvedeného integrálu objeví kombinace \(\cos\left(\frac{\pi x}{L}\right)\,\sin\left(\frac{2\pi x}{L}\right)\), což je součin dvou vlastních funkcí hamiltoniánu. Tyto funkce jsou ortogonální – integrál z jejich součinu (pravděpodobnost „překrytí” těchto dvou stavů) je roven nule. Proto můžeme itegrál dále počítat bez nich. Zjednoduší se na
\[ \langle E(t) \rangle = \frac{2}{5L} \int_{-\frac{L}{2}}^{\frac{L}{2}} \left[ 4E_1 \,\cos^2 \left( \frac{\pi x}{L} \right) \,+\, E_2 \,\sin^2\left(\frac{2\pi x}{L}\right) \right] \,\mbox{d}x\,. \]Užitím vztahů pro sinus a kosinus polovičního argumentu upravíme výraz do tvaru
\[ \langle E(t) \rangle = \frac{4E_1}{5L}\int_{-\frac{L}{2}}^{\frac{L}{2}} \left[1\,+\,\cos\left(\frac{2\pi x}{L}\right)\right]\,\mbox{d}x \,+\, \frac{E_2}{5L}\int_{-\frac{L}{2}}^{\frac{L}{2}} \left[1\,-\,\cos\left(\frac{4\pi x}{L}\right)\right]\,\mbox{d}x\,, \]
\[ \langle E(t) \rangle = \frac{4E_1}{5L}\,\left[x\,+\,\frac{L}{2\pi}\sin\left(\frac{2\pi x}{L}\right)\right]_{-\frac{L}{2}}^{\frac{L}{2}} \,+\, \frac{E_2}{2L}\,\left[x\,-\,\frac{L}{4\pi}\cos\left(\frac{4\pi x}{L}\right)\right]_{-\frac{L}{2}}^{\frac{L}{2}} \,, \]
\[ \langle E(t) \rangle = \frac{4E_1}{5L}\,\cdot\,L \,+\,\frac{E_2}{5L}\,\cdot\,L\,, \]
\[ \langle E(t) \rangle = \frac{4}{5} \,E_1 \,+\, \frac{1}{5} \,E_2 = \frac{8}{5}\,E_1\,,\] kde \( E_1 = \frac{\pi^2 \hbar^2}{2mL^2} \).
Nápověda ke 2 – rozklad do báze ortogonálních funkcí
Můžeme při výpočtu střední hodnoty energie využít faktu, že vlastní funkce hamiltoniánu tvoří ortogonální systém?
Řešení 2 – druhá verze (z ortogonálního rozkladu)
V řešení předcházející nápovědy jsme odvodili, že pokud vlnovou funkci \(\psi(x,\,t)\) vyjádříme jako součet navzájem ortogonálních normovaných vlastních funkcí \(\psi_n(x,\,t)\) operátoru \(\hat{H}\,,\) \[\psi(x,\,t)=\sum_{n=1}^{\infty}a_n \psi_n(x,\,t)\,,\] je střední hodnota energie částice v libovolném čase t rovna
\[\langle E(t) \rangle =\sum_{n=1}^{\infty}|a_n|^2 E_n\,. \]Jak jsme připomněli v řešení úkolu 1), stacionární stavy částice v dané potenciálové jámě jsou popsány funkcemi
\(\hspace{25px}\psi_n(x,\,t)=\sqrt{\frac{2}{L}}\, \cos\left(\frac{n\pi x}{L}\right)\,e^{-\frac{iE_n t}{\hbar}}\) pro n lichá a
\(\hspace{25px}\psi_n(x,\,t)=\sqrt{\frac{2}{L}}\, \sin\left(\frac{n\pi x}{L}\right)\,e^{-\frac{iE_n t}{\hbar}}\) pro n sudá.
Jim odpovídají energie \[E_n=\frac{n^2 \pi^2 \hbar^2}{2mL^2}\,.\]
V úkolu 1) jsme také našli předpis pro vlnovou funkci v obecném čase t:
\[\psi(x,\,t)=\frac{2}{\sqrt{5}}\,\psi_1(x)\,e^{-\frac{iE_1 t}{\hbar}}+\,\frac{1}{\sqrt{5}}\,\psi_2(x)\,e^{-\frac{iE_2 t}{\hbar}}\,.\]Platí \[ \psi(x,\,t) = \frac{2}{\sqrt{5}}\,\sqrt{\frac{2}{L}}\,\cos\left(\frac{\pi x}{L}\right)\,e^{-\frac{iE_1 t}{\hbar}} \,+\,\frac{1}{\sqrt{5}}\,\sqrt{\frac{2}{L}}\,\sin\left(\frac{2\pi x}{L}\right)\,e^{-\frac{iE_2 t}{\hbar}}\,, \]
což je lineární kombinace normovaných vlnových funkcí prvních dvou stacionárních stavů:
\[\psi(x,\,t) = \frac{2}{\sqrt{5}}\,\psi_1(x,\,t)\,+\,\frac{1}{\sqrt{5}}\,\psi_2(x,\,t)\,, \]je proto
\[ \langle E(t) \rangle = \sum_{n=1}^{2} E_n |a_n|^2=E_1 |a_1|^2 \,+\, E_2 |a_2|^2\,, \] \[ \langle E(t) \rangle = E_1 \,\left(\frac{2}{\sqrt{5}}\right)^2 +\, E_2 \,\left(\frac{1}{\sqrt{5}}\right)^2\,, \] \[ \langle E(t) \rangle = \frac{4}{5} \,E_1 \,+\, \frac{1}{5} \,E_2 = \frac{8}{5}\,E_1\,,\] kde \[ E_1 = \frac{\pi^2 \hbar^2}{2mL^2}\,. \]Nápověda ke 3
Stav částice, jejíž pohyb je vázán na úsečku <-L/2, L/2>, je v čase t je popsán vlnovou funkcí
\[\psi(x,\,t)=\sqrt{\frac{2}{5L}}\,\left[2\, \cos\left(\frac{\pi x}{L}\right)\,e^{-\frac{iE_1 t}{\hbar}}+\,\sin\left(\frac{2\pi x}{L}\right)\,e^{-\frac{i4E_1 t}{\hbar}}\right]\,.\]Pravděpodobnost výskytu částice na intervalu (a,b) je rovna integrálu hustoty pravděpodobnosti (tj. čtverce absolutní hodnoty vlnové funkce ψ(x,t)) přes tento interval.
Řešení 3
a) Pravděpodobnost výskytu částice na obecném intervalu (a,b) uvnitř jámy je
\[ P(x\in (a,\,b),\,t)=\int_a^b |\psi(x,\,t)|^2\,\mbox{d}x\,,\] \[ P=\int_a^b \frac{2}{5L}\,\left| 2\, \cos\left(\frac{\pi x}{L}\right)\,e^{-\frac{iE_1 t}{\hbar}}\,+\,\sin\left(\frac{2\pi x}{L}\right)\,e^{-\frac{i4E_1 t}{\hbar}}\right|^2\,\mbox{d}x\,,\] \[P=\frac{2}{5L}\int_a^b \left[4\,\cos^2\left(\frac{\pi x}{L}\right)+\,\sin^2\left(\frac{2\pi x}{L}\right)\right]\,\mbox{d}x\,+\,\frac{2}{5L}\int_a^b 4\,\cos\left(\frac{\pi x}{L}\right)\,\sin\left(\frac{2\pi x}{L}\right)\,\cos\left(\frac{3E_1 t}{\hbar}\right)\,\mbox{d}x\,.\]Dále užitím vztahů pro sinus a kosinus polovičního argumentu a vztahu pro sinus dvojnásobného argumentu dostáváme
\[P=\frac{1}{5L}\int_a^b \left[5\,+\,\cos\left(\frac{2\pi x}{L}\right)\,-\,\cos\left(\frac{4\pi x}{L}\right)\right]\,\mbox{d}x\,+\,\frac{2}{5L}\int_a^b 8\,\cos^2\left(\frac{\pi x}{L}\right)\,\sin\left(\frac{\pi x}{L}\right)\,\cos\left(\frac{3E_1 t}{\hbar}\right)\,\mbox{d}x\,,\]což po zintegrování dává
\[P=\frac{1}{5L}\,\left[ 5x\,+\,\frac{L}{2\pi}\,\sin\left(\frac{2\pi x}{L}\right)\,-\,\frac{L}{4\pi}\,\sin\left(\frac{4\pi x}{L}\right)\right]_a^b\,-\,\frac{16}{5L}\,\left[\frac{L}{3\pi}\,\cos^3\left(\frac{\pi x}{L}\right)\,\cos\left(\frac{3E_1 t}{\hbar}\right)\right]_a^b\,,\] \[P=\left[ \frac{x}{L}\,+\,\frac{1}{10\pi}\,\sin\left(\frac{2\pi x}{L}\right)\,-\,\frac{1}{20\pi}\,\sin\left(\frac{4\pi x}{L}\right)\right]_a^b\,-\,\frac{16}{15\pi}\,\left[\cos^3\left(\frac{\pi x}{L}\right)\,\cos\left(\frac{3E_1 t}{\hbar}\right)\right]_a^b\,.\]b) Pravděpodobnost nalezení částice na intervalu (0, L/2) získáme dosazením do výsledku a):
\[P=\left[ \frac{x}{L}\,+\,\frac{1}{10\pi}\,\sin\left(\frac{2\pi x}{L}\right)\,-\,\frac{1}{20\pi}\,\sin\left(\frac{4\pi x}{L}\right)\right]_{0}^{L/2}\,-\,\frac{16}{15\pi}\,\left[\cos^3\left(\frac{\pi x}{L}\right)\,\cos\left(\frac{3E_1 t}{\hbar}\right)\right]_{0}^{L/2}\,,\] \[P=\frac{1}{2}\,+\,\frac{16}{15\pi}\,\cos\left(\frac{3E_1 t}{\hbar}\right)\,.\]Pravděpodobnost výskytu částice v pravé části jámy se mění s časem. Osciluje mezi hodnotami \(\frac{1}{2}\,-\,\frac{16}{15\pi}\,\dot{=}\,0{,}16\) a \(\frac{1}{2}\,+\,\frac{16}{15\pi}\,\dot{=}\,0{,}84\). Maxima nabývá v časech \(t_{max}=2k\,\cdot\,\frac{\pi \hbar}{3E_1}\) a minima v časech \(t_{min}=(2k+1)\,\cdot\,\frac{\pi \hbar}{3E_1}\), kde k = 0, 1, 2, ... a \(E_1=\frac{\pi^2 \hbar^2}{2mL^2}\).
c) Pravděpodobnost nalezení částice na intervalu (−L/4, L/4) získáme dosazením do výsledku a):
\[P=\left[ \frac{x}{L}\,+\,\frac{1}{10\pi}\,\sin\left(\frac{2\pi x}{L}\right)\,-\,\frac{1}{20\pi}\,\sin\left(\frac{4\pi x}{L}\right)\right]_{-L/4}^{L/4}\,-\,\frac{16}{15\pi}\,\left[\cos^3\left(\frac{\pi x}{L}\right)\,\cos\left(\frac{3E_1 t}{\hbar}\right)\right]_{-L/4}^{L/4}\,,\] \[P=\frac{1}{2}\,+\,\frac{1}{5\pi}\,\dot{=}\,0{,}56\,.\]Pravděpodobnost výskytu částice ve střední části jámy je nezávisle na čase rovna přibližně 56 %. Časová nezávislost je u nestacionárního stavu spíše výjimečná (jak je vidět z obecného řešení v části a)). Zde je důsledkem symetrie zvoleného intervalu vzhledem ke středu jámy.
Odpovědi
1) Vlnová funkce
\[\psi(x,\,t)=\sqrt{\frac{2}{5L}}\,\left[2\, \cos\left(\frac{\pi x}{L}\right)\,e^{-\frac{iE_1 t}{\hbar}}\,+\,\sin\left(\frac{2\pi x}{L}\right)\,e^{-\frac{i4E_1 t}{\hbar}}\right]\,,\]kde \(E_1=\frac{\pi^2 \hbar^2}{2mL^2}\).
2) Střední hodnota energie částice je \(\langle E(t) \rangle=\frac{8}{5}\,E_1\,,\) kde \(E_1=\frac{\pi^2 \hbar^2}{2mL^2}\).
3a) Pravděpodobnost, že se částice v čase t nachází někde na intervalu (a,b) uvnitř jámy, je rovna
\[P=\left[ \frac{x}{L}\,+\,\frac{1}{10\pi}\,\sin\left(\frac{2\pi x}{L}\right)\,-\,\frac{1}{20\pi}\,\sin\left(\frac{4\pi x}{L}\right)\right]_a^b\,-\,\frac{16}{15\pi}\,\left[\cos^3\left(\frac{\pi x}{L}\right)\,\cos\left(\frac{3E_1 t}{\hbar}\right)\right]_a^b\,.\]3b) Pravděpodobnost výskytu částice v pravé části jámy na intervalu (0, L/2) je \(P=\frac{1}{2}\,+\,\frac{16}{15\pi}\,\cos\left(\frac{3E_1 t}{\hbar}\right)\). Mění se s časem mezi hodnotami 16% a 84%. Maxima nabývá v časech \(t_{max}=2k\,\cdot\,\frac{\pi \hbar}{3E_1}\) a minima v časech \(t_{min}=(2k+1)\,\cdot\,\frac{\pi \hbar}{3E_1}\), kde k = 0, 1, 2, ... a \(E_1=\frac{\pi^2 \hbar^2}{2mL^2}\,.\)
3c) Pravděpodobnost výskytu částice v prostřední části jámy na intervalu (-L/4, L/4) je v libovolném čase t rovna \(P=\frac{1}{2}\,+\,\frac{1}{5\pi}\), což je asi 56 %.
Časová nezávislost je u nestacionárního stavu spíše výjimečná (jak je vidět z obecného řešení v části a)). Zde je důsledkem symetrie zvoleného intervalu vzhledem ke středu jámy.
Odkaz
Podobný problém se řeší také v úlohách Superpozice dvou vlastních stavů a Superpozice tří vlastních stavů této sbírky.


