Elektron v krystalu soli
Úloha číslo: 685
Krystalová mřížka NaCl obsahuje několik záporných vakancí, z nichž každá odpovídá jednomu elektronu. Považujte tyto elektrony za volně se pohybující do vzdálenosti řádově odpovídající mřížkové konstantě. Krystal se nachází v místě o pokojové teplotě za normálního tlaku. Odhadněte maximální vlnovou délku elektromagnetického záření, které tyto elektrony mohou absorbovat při přechodu mezi dvěma sousedními hladinami energie.
Nápověda 1
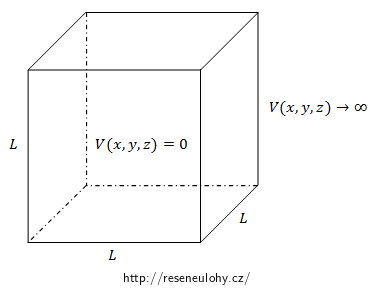
Mřížková konstanta v krystalu NaCl je rovna 564 pm. Charakteristický rozměr krychle, v níž je elektron uvězněn, můžeme odhadnout na L = 560 pm (jde pouze o řádový odhad, proto je přesnost na dvě platné číslice víc než dostačující). Jelikož předpokládáme, že nemůže z této oblasti uniknout, můžeme si situaci představit jako elektron uvězněný v nekonečně hluboké třírozměrné potenciálové jámě tvaru krychle o hraně délky L.
Nápověda 2
Závislost energie na hmotnosti částice, šířce jámy a dalších parametrech je u třírozměrného problému obdobná jako u analogické situace v jednom rozměru. Kvantování energie je složitější pouze tím, že si vyžaduje použití tří kvantových čísel nx, ny a nz místo jednoho čísla n. Jak tedy přesně vypadá předpis pro Enx ny nz?
Nápověda 3
Jak závisí energie záření na jeho vlnové délce?
Nápověda 4
Kvantum energie nesené zářením o vlnové délce \(\lambda\) je rovno \(\Delta E=\frac{hc}{\lambda}\).
Jestliže hledáme co nejdelší možnou vlnovou délku absorbovaného záření, jaké energetické rozdíly mezi jednotlivými hladinami nás budou zajímat?
Řešení – 1. část
Možné energie elektronu jsou
\[E_{n_x^{\,} n_y n_z}=\frac{\pi^2 \hbar^2}{2mL^2}\,\left(n_x^2 + n_y^2 + n_z^2 \right) ,\]kde nx, ny, nz = 1, 2, 3, ... . Úkolem je nyní najít takové dvě hladiny, jejichž rozdíl je minimální. Vzhledem k tomu, že nx, ny, nz jsou přirozená čísla, je každý možný energetický rozdíl dvou hladin násobkem hodnoty \[\frac{\pi^2 \hbar^2}{2mL^2} .\] Proto musíme najít dvě takové trojice přirozených čísel nx, ny, nz, pro které platí, že součet kvadrátů čísel z první trojice a součet kvadrátů čísel z druhé trojice se liší co nejméně, ideálně o 1.
Řešení – 2. část
V následující tabulce jsou vypsány (neuspořádané) trojice přirozených čísel, pro které je součet jejich kvadrátů menší než 30. (30 je náhodně zvolené číslo, mohli bychom samozřejmě pokračovat i přes 30.)
nx ny nz nx2 + ny2 + nz2 1 1 1 3 1 1 2 6 1 1 3 11 1 1 4 18 1 1 5 27 1 2 2 9 1 2 3 14 1 2 4 21 1 3 3 19 1 3 4 26 2 2 2 12 2 2 3 17 2 2 4 24 2 3 3 22 2 3 4 29 3 3 3 27 Seřazeno vzestupně, prvních 15 energetických hladin má hodnoty 3, 6, 9, 11, 12, 14, 17, 18, 19, 21, 22, 24, 26, 27, 29 krát \(\frac{\pi^2 \hbar^2}{2mL^2}\) (většina je několikrát degenerovaná).
Určitě tedy existují sousední energetické hladiny (např. dvojice E113 a E222 nebo E223 a E114 atd.), jejichž rozdíl je nejmenší možný, tj. \[\Delta E=\frac{\pi^2 \hbar^2}{2mL^2} .\]
Řešení – 3. část
Zjistili jsme tedy, že nejmenší možný rozdíl dvou různých energetických hladin elektronu v nekonečně hluboké krychlové potenciálové jámě o hraně délky L je roven \[\Delta E=\frac{\pi^2 \hbar^2}{2m_e L^2} .\] Takové kvantum energie může elektronu předat záření o vlnové délce \[\lambda=\frac{hc}{\Delta E} .\] Spojením těchto dvou vztahů dostáváme
\[\lambda=\frac{hc\,2m_e L^2}{\pi^2 \hbar^2} ,\] \[\lambda=\frac{2\pi\hbar c\,2m_e L^2}{\pi^2 \hbar^2} ,\] \[\lambda=\frac{4c m_e L^2}{\pi \hbar} ,\] \[\lambda=\frac{4\,\cdot\,3\,\cdot\,10^8\,\cdot\,9{,}11\,\cdot\,10^{-31}\,\cdot\,\left(560\,\cdot\,10^{-12}\right)^2}{\pi\,\cdot\,1{,}055\,\cdot\,10^{-34}}\ \mbox{m}=\frac{12\,\cdot\,9{,}11\,\cdot\,560^2}{\pi\,\cdot\,1{,}055}\ 10^{-13}\ \mbox{m}\,\dot{=}\, 1{,}0\,\cdot\,10^{-6}\ \mbox{m}=1{,}0 \,\mathrm{\mu m},\]což je vlnová délka blízkého infračerveného záření.
Odpověď
Maximální vlnová délka elektromagnetického záření, které mohou v tomto modelu elektrony v NaCl absorbovat, je přibližně 1,0 µm.


