Stupňovitá pravoúhlá jáma
Úloha číslo: 705
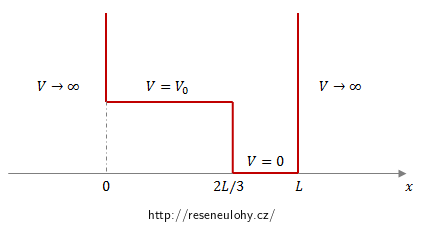
Částice se nachází uvnitř nekonečně hluboké potenciálové jámy znázorněné na obrázku níže. Její stav je v čase t = 0 popsán vlnovou funkcí
\[\psi(x)=\sqrt{\frac{2}{L}}\ \sin\left(\frac{3\pi x}{L}\right)\] pro \(x \in \langle 0,\,L\rangle\) a
\(\psi(x)=0\) pro \(x \not\in \langle 0,\,L\rangle\).
1) Rozhodněte, zda je \(\psi(x)\) vlastní funkcí hamiltoniánu.
2) Vypočtěte střední hodnotu polohy \(\langle \hat{x} \rangle\) v čase t = 0.
3) Vypočtěte střední hodnotu hybnosti \(\langle \hat{p}_x \rangle\) v čase t = 0.
4) Vypočtěte střední hodnotu energie \(\langle \hat{H} \rangle\) v čase t = 0.
Nápověda k 1
Jaký tvar má Schrödingerova rovnice v „levé” části jámy a jaký tvar má v „pravé“ části jámy?
Řešení 1
V „levé” části potenciálové jámy má Schrödingerova rovnice po úpravě tvar
\[\frac{\mbox{d}^2 \psi(x)}{\mbox{d} x^2}\,+\,\frac{2m(E-V_0)}{\hbar^2}\,\psi(x)=0\,.\]V „pravé” části potenciálové jámy má tvar
\[\frac{\mbox{d}^2 \psi(x)}{\mbox{d} x^2}\,+\,\frac{2mE}{\hbar^2}\,\psi(x)=0\,.\]Má-li být nějaká funkce vlastní funkcí hamiltoniánu uvnitř jámy, pak musí být jeho vlastní funkcí v „levé“ i „pravé“ části jámy.
Dosazením zadané funkce
\[\psi(x)=\sqrt{\frac{2}{L}}\ \sin\left(\frac{3\pi x}{L}\right)\]do obou uvedených rovnic dostáváme
\[-\frac{9\pi^2}{L^2}\,\sqrt{\frac{2}{L}}\,\sin\left(\frac{3\pi x}{L}\right)\,+\,\frac{2m(E-V_0)}{\hbar^2}\,\sqrt{\frac{2}{L}}\,\sin\left(\frac{3\pi x}{L}\right)=0\,,\]po úpravě
\[\sqrt{\frac{2}{L}}\,\sin\left(\frac{3\pi x}{L}\right)\left(-\frac{9\pi^2}{L^2}\,+\,\frac{2m(E-V_0)}{\hbar^2}\right)=0\tag{1}\]a zároveň
\[-\frac{9\pi^2}{L^2}\,\sqrt{\frac{2}{L}}\,\sin\left(\frac{3\pi x}{L}\right)\,+\,\frac{2mE}{\hbar^2}\,\sqrt{\frac{2}{L}}\,\sin\left(\frac{3\pi x}{L}\right)=0\,,\]po úpravě
\[\sqrt{\frac{2}{L}}\,\sin\left(\frac{3\pi x}{L}\right)\left(-\frac{9\pi^2}{L^2}\,+\,\frac{2mE}{\hbar^2}\right)=0\,.\tag{2}\]Rovnice (1) a (2) si ale protiřečí, neboť pro V0 > 0 nemůže být zároveň
\(E=V_0 \,+\, \frac{9\pi^2 \hbar^2}{2mL^2}\ \) a \(\,E=\frac{9\pi^2 \hbar^2}{2mL^2}\).
Z toho vyplývá, že uvedená funkce ψ(x) není vlastní funkcí hamiltoniánu.
Nápověda k 2, 3 a 4
Pro částici, jejíž stav je v daném čase popsán vlnovou funkcí \(\psi(x)\), je střední hodnota operátoru \(\hat{O}\) definována jako integrál
\[\langle \hat{O} \rangle = \int_{-\infty}^{\infty} \psi^*(x)\,\hat{O}\psi(x)\,\mbox{d}x\,.\]Řešení 2
Střední hodnota polohy je v čase t = 0 rovna
\[\langle \hat{x} \rangle = \int_{-\infty}^{\infty} \psi^*(x)\,x\psi(x)\,\mbox{d}x\,.\]Dosazením za \(\psi(x)\) dostáváme
\[\langle \hat{x} \rangle = \frac{2}{L}\int_0^L x\,\sin^2\left(\frac{3\pi x}{L}\right)\,\mbox{d}x\,,\] \[\langle \hat{x} \rangle = \frac{1}{L}\int_0^L x\,\left[1\,-\,\cos\left(\frac{6\pi x}{L}\right)\right]\,\mbox{d}x\]a dále metodou per partes
\[\langle \hat{x} \rangle = \frac{1}{L}\,\left[\frac{x^2}{2}\right]_0^L -\,\frac{1}{L}\,\left[\frac{L}{6\pi}\,x\,\sin\left(\frac{6\pi x}{L}\right)\right]_0^L -\,\frac{1}{L}\,\left[\frac{L^2}{36\pi^2}\,\cos\left(\frac{6\pi x}{L}\right)\right]_0^L\,= \frac{L}{2}\,.\]Řešení 3
Střední hodnota hybnosti částice je v čase t = 0 rovna
\[\langle \hat{p}_x \rangle = \int_{-\infty}^{\infty} \psi^*(x)\,(-i\hbar)\frac{\mbox{d}\psi(x)}{\mbox{d}x}\,\mbox{d}x\,.\]Dosazením za ψ(x) dostáváme
\[\langle \hat{p}_x \rangle =\frac{2}{L}\int_0^L \sin\left(\frac{3\pi x}{L}\right)\,(-i\hbar)\left[\frac{\mbox{d}}{\mbox{d}x}\,\sin\left(\frac{3\pi x}{L}\right)\right]\,\mbox{d}x\,,\] \[\langle \hat{p}_x \rangle =-\frac{2i\hbar}{L}\int_0^L \sin\left(\frac{3\pi x}{L}\right)\,\left[\frac{\mbox{d}}{\mbox{d}x}\,\sin\left(\frac{3\pi x}{L}\right)\right]\,\mbox{d}x\,.\tag{3}\]Tento integrál je jako stvořený pro substituci. Označme
\[t=\sin\left(\frac{3\pi x}{L}\right)\,.\]Pak je
\[\mbox{d}t=\left[\frac{\mbox{d}}{\mbox{d}x}\,\sin\left(\frac{3\pi x}{L}\right)\right]\,\mbox{d}x\]a integrál (3) můžeme počítat jako
\[\langle \hat{p}_x \rangle = -\frac{2i\hbar}{L}\int_0^0 t\,\mbox{d}t=0\,.\]Řešení 4
Střední hodnotu hamiltoniánu vypočteme klasicky z definice. Platí
\[\langle \hat{H} \rangle = \int_0^L \psi^*(x)\,\hat{H}\psi(x)\,\mbox{d}x\,,\] \[\langle \hat{H} \rangle = \int_0^L \psi^*(x)\,(\hat{T}+\hat{V})\psi(x)\,\mbox{d}x\,.\]Vzhledem k linearitě integrálu ho můžeme rozdělit na součet dvou
\[\langle \hat{H} \rangle = \int_0^L \psi^*(x)\,\hat{T}\psi(x)\,\mbox{d}x\,+\int_0^L \psi^*(x)\,\hat{V}\psi(x)\,\mbox{d}x\,.\]Vzhledem k nulové potenciální energii na intervalu (2L/3, L) můžeme změnit meze druhého integrálu a psát
\[\langle \hat{H} \rangle = \int_0^L \psi^*(x)\,\hat{T}\psi(x)\,\mbox{d}x\,+\int_0^{2L/3} \psi^*(x)\,\hat{V}\psi(x)\,\mbox{d}x\,.\]Nyní dosadíme za kinetickou a potenciální energii odpovídající výrazy:
\[\langle \hat{H} \rangle = \int_0^{L} \psi^*(x)\,\left(-\frac{\hbar^2}{2m}\right)\,\frac{\mbox{d}^2 \psi(x)}{\mbox{d}x^2} \,\mbox{d}x\,+\int_0^{2L/3} \psi^*(x)\,V_0\,\psi(x)\,\mbox{d}x\,,\] \[\langle \hat{H} \rangle = V_0 \int_0^{2L/3} |\psi(x)|^2\,\mbox{d}x\,-\,\frac{\hbar^2}{2m}\int_{0}^L \psi^*(x)\,\frac{\mbox{d}^2 \psi(x)}{\mbox{d}x^2}\,\mbox{d}x\,.\]Dosazením vlnové funkce
\[\psi(x)=\sqrt{\frac{2}{L}}\ \sin\left(\frac{3\pi x}{L}\right)\]dostáváme
\[\langle \hat{H} \rangle=\frac{2V_0}{L}\int_0^{2L/3} \sin^2\left(\frac{3\pi x}{L}\right)\mbox{d}x\,-\,\frac{\hbar^2}{2m}\frac{2}{L}\,\left(-\frac{9\pi^2}{L^2}\right)\int_0^L \sin^2\left(\frac{3\pi x}{L}\right)\mbox{d}x. \]Užitím vztahu pro sinus polovičního argumentu upravíme integrály do tvaru
\[\langle \hat{H} \rangle=\frac{V_0}{L}\int_0^{2L/3} \left[1-\cos\left(\frac{6\pi x}{L}\right)\right]\,\mbox{d}x\,+\, \frac{9\pi^2\hbar^2}{2mL^3}\int_0^L \left[1-\cos\left(\frac{6\pi x}{L}\right)\right]\,\mbox{d}x\,, \] \[\langle \hat{H} \rangle=\frac{V_0}{L}\, \left[x-\frac{L}{6\pi}\,\sin\left(\frac{6\pi x}{L}\right)\right]_0^{2L/3}+\, \frac{9\pi^2\hbar^2}{2mL^3}\,\left[x-\frac{L}{6\pi}\,\sin\left(\frac{6\pi x}{L}\right)\right]_0^L\,, \] \[\langle \hat{H} \rangle= \frac{2V_0}{3}\,+\,\frac{9\pi^2\hbar^2}{2mL^2}\,.\]Odpovědi
1) Funkce ψ(x) není vlastní funkcí hamiltoniánu.
2) Střední hodnota polohy částice je v čase t = 0 rovna \(\langle \hat{x} \rangle = \frac{L}{2}\) (střed jámy).
3) Střední hodnota hybnosti částice je v čase t = 0 rovna \(\langle \hat{p}_x \rangle = 0\).
4) Střední hodnota energie částice je v čase t = 0 rovna \(\langle \hat{H} \rangle= \frac{2V_0}{3}\,+\,\frac{9\pi^2\hbar^2}{2mL^2}\).
Aplet
Pokud vás zajímá, jak asi vypadají vlastní funkce hamiltoniánu v jámě tohoto typu, otevřete si stránku http://webphysics.davidson.edu/physletprob/ch10_modern/default.html a prozkoumejte aplet dostupný v levém menu pod názvem Finite Well. Do prázdného pole Potential, které se nachází pod grafem, napište například
2000-step(x+0.75)*1500-step(x-0.25)*500+step(x-0.75)*2000,čímž vytvoříte stupňovitou potenciálovou jámu podobnou té, s níž jsme počítali v této úloze. Stejná být nemůže už jen proto, že výše potenciálu na levé a pravé straně je omezená a jde tedy vždy o konečně hlubokou jámu. Na druhou stranu, exponenciální pokles v klasicky nedostupné oblasti je poměrně rychlý a průběh vlnové funkce ani hladiny energie se pro malá n nebudou dramaticky lišit od řešení pro jámu nekonečně hlubokou. Hodnoty kvantového čísla n volte postupně od 1 do 20 (pro 21 a vyšší se již dostanete mimo rozsah zobrazované oblasti).
Sledujte, jak se mění tvar vlnové funkce a jak se posouvají energetické hladiny. Osa, kolem které „sinusoida“ vlnové funkce osciluje, je pro názornost posunuta vždy na úroveň dané energie.


