Symetrická nekonečná pravoúhlá jáma
Úloha číslo: 720
Částice o hmotnosti m se nachází v nekonečně hluboké pravoúhlé potenciálové jámě šířky L: V(x) = 0 pro |x| ≤ L/2 a V(x) → ∞ pro |x| > L/2.
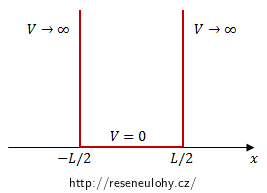
Najděte normované vlastní funkce a vlastní čísla hamiltoniánu pro tento případ.
Nápověda
Pohyb částice je omezen na interval <−L/2, L/2> a mimo tento interval se nemůže vyskytovat, tj. mimo tento interval je vlnová funkce identicky rovna nule. Řešte nečasovou Schrödingerovu rovnici na intervalu <−L/2, L/2>.
Řešení Schrödingerovy rovnice
Mimo interval <−L/2, L/2> je vlnová funkce identicky rovna nule. Budeme tedy řešit nečasovou Schrödingerovu rovnici pro částici uvnitř tohoto intervalu, kde je V = 0 a energie částice je rovna její kinetické energii. Rovnice má tvar
\[-\frac{\hbar^2}{2m}\,\frac{\mbox{d}^2 \psi(x)}{\mbox{d}x^2}=E\psi(x)\,,\]po úpravě
\[\frac{\mbox{d}^2 \psi(x)}{\mbox{d}x^2}\,+\,\frac{2mE}{\hbar^2}\,\psi(x)=0\,.\]Protože m > 0, ħ > 0 a E > 0, můžeme označit \(\frac{2mE}{\hbar^2}=k^2\), kde k > 0.Obecné řešení diferenciální rovnice
\[\frac{\mbox{d}^2 \psi(x)}{\mbox{d}x^2}\,+\,k^2\,\psi(x)=0\]lze zapsat ve tvaru
\[\psi(x)=Ae^{ikx}\,+\,Be^{-ikx}\,,\]kde A, B jsou libovolná, zatím blíže neurčená komplexní čísla.
Nápověda – vlnová funkce
Jaké podmínky musí vlnová funkce splňovat?
Hledání vlnové funkce
Podle postulátu o vlnové funkci požadujeme, aby vlnová funkce byla spojitá. Vzhledem k tomu, že platí ψ(x) = 0 pro |x| > L/2, musí být splněny okrajové podmínky ψ(−L/2) = 0 a ψ(L/2) = 0. Z těch dostáváme dvojici rovnic
\[Ae^{-\frac{ikL}{2}}+Be^{\frac{ikL}{2}}=0\,,\] \[Ae^{\frac{ikL}{2}}+Be^{-\frac{ikL}{2}}=0\,.\]Vyjádřením poměru B/A z každé z nich a následným porovnáním dostáváme rovnost
\[\frac{B}{A}=-e^{-ikL}=-e^{ikL}\,.\]Aby toto platilo, musí být \(\,ikL=-ikL+i2n\pi\), kde n je přirozené číslo. Odtud po úpravě \(k=\frac{n\pi}{L}\). Pro poměr B/A tedy platí
\[\frac{B}{A}=-e^{ikL}=-e^{in\pi}=(-1)^{n+1}\,.\]Pro n lichá tak dostáváme
\[\psi(x)=A\,\left(e^{\frac{in\pi x}{L}}\,+\,e^{-\frac{in\pi x}{L}}\right)\,,\]zatímco pro n sudá
\[\psi(x)=A\,\left(e^{\frac{in\pi x}{L}}\,-\,e^{-\frac{in\pi x}{L}}\right)\,.\]S využitím známých Eulerových vzorců
\[\cos\alpha=\frac{e^{i\alpha}\,+\,e^{-i\alpha}}{2},\ \ \sin\alpha=\frac{e^{i\alpha}\,-\,e^{-i\alpha}}{2i}\]můžeme vlnovou funkci zapsat ve tvaru
\(\psi_n(x)=N\cos\left(\frac{n\pi x}{L}\right)\) pro n lichá a
\(\psi_n(x)=N\sin\left(\frac{n\pi x}{L}\right)\) pro n sudá,
kde N je vhodná normovací konstanta.
Nápověda – normování
Co to znamená normovat vlnovou funkci (jde-li o funkci jedné souřadnicové proměnné x?
Řešení – normování
Pravděpodobnost výskytu částice někde na ose x (jde o jednorozměrný problém) musí být rovna jedné. Jelikož je pohyb částice omezen na úsečku <−L/2, L/2>, musí být pravděpodobnost rovna 1 právě na tomto intervalu. Pravděpodobnost spočítáme jako integrál z hustoty pravděpodobnosti, které odpovídá kvadrát absolutní hodnoty vlnové funkce. Normovací podmínka má proto tvar
\[\int_{-L/2}^{L/2} |\psi_n(x)|^2\,\mbox{d}x=1\,.\]Pro n lichá máme
\[1=\int_{-L/2}^{L/2} |N|^2 \,\cos^2\left(\frac{n\pi x}{L}\right)\,\mbox{d}x\,,\] \[\frac{1}{|N|^2}=\int_{-L/2}^{L/2}\frac{1}{2}\left[ 1\,+\,\cos\left(\frac{2n\pi x}{L}\right)\right]\,\mbox{d}x\,,\] \[\frac{2}{|N|^2}=\left[ x\,+\,\frac{L}{2n\pi}\,\sin\left(\frac{2n\pi x}{L}\right)\right]_{-L/2}^{L/2}\,,\] \[\frac{2}{|N|^2}=L\,,\]odkud můžeme volit \(N=\sqrt{\frac{2}{L}}\).
Stejně tak pro n sudá máme
\[1=\int_{-L/2}^{L/2} |N|^2 \,\sin^2\left(\frac{n\pi x}{L}\right)\,\mbox{d}x\,,\] \[\frac{1}{|N|^2}=\int_{-L/2}^{L/2}\frac{1}{2}\left[ 1\,-\,\cos\left(\frac{2n\pi x}{L}\right)\right]\,\mbox{d}x\,,\] \[\frac{2}{|N|^2}=\left[ x\,-\,\frac{L}{2n\pi}\,\sin\left(\frac{2n\pi x}{L}\right)\right]_{-L/2}^{L/2}\,,\] \[\frac{2}{|N|^2}=L\,,\]odkud můžeme také volit \(N=\sqrt{\frac{2}{L}}\).
Nápověda – energie
Na začátku řešení této úlohy jsme substituovali \(\frac{2mE}{\hbar^2}=k^2\). Dále jsme zjistili, že k může vzhledem k požadavkům kladeným na vlnovou funkci nabývat jen některých vybraných hodnot.
Řešení – energie
Na začátku řešení této úlohy jsme substituovali \(\frac{2mE}{\hbar^2}=k^2\). Dále jsme zjistili, že \(k=\frac{n\pi}{L}\), n = 1, 2, ... . Z prvního vztahu vyjádříme energii E a dosadíme za k.
Pro energii stavu s kvantovým číslem n tak dostáváme
\(\hspace{40px}E_n=\frac{\hbar^2 k^2}{2m}=\frac{n^2 \pi^2 \hbar^2}{2mL^2}\), n = 1, 2, ...
Odpověď
Pro případ částice o hmotnosti m v nekonečně hluboké pravoúhlé potenciálové jámě šířky L, jejíž střed má souřadnici x = 0, jsme našli normované vlastní funkce hamiltoniánu
\(\hspace{40px}\psi_n(x)=\sqrt{\frac{2}{L}}\, \cos\left(\frac{n\pi x}{L}\right)\) pro n lichá a
\(\hspace{40px}\psi_n(x)=\sqrt{\frac{2}{L}}\, \sin\left(\frac{n\pi x}{L}\right)\) pro n sudá,
kterým přísluší vlastní čísla
\(\hspace{40px}E_n=\frac{n^2 \pi^2 \hbar^2}{2mL^2}\), n = 1, 2, ... .


