Sbírka řešených úloh

Časově konstantní porucha

Úloha číslo: 2290

• Nápověda 1

  Připomeňte si princip nestacionární poruchové metody v kvantové mechanice.

• Řešení nápovědy 1

  Předpokládejme hamiltonián ve tvaru

  \[\hat{H}(t)=\hat{H_0}+\lambda\hat{W}(t),\]

  kde \(\hat{H_0}\) je neporušený hamiltonián, který je časově nezávislý, \(\lambda\) je malý parametr, který jsme vytknuli z poruchového členu. Jelikož je poruchový člen časově závislý, je závislý i porušený hamiltonián.

  Dále předpokládáme stacionární řešení neporušené stacionární Schrödingerovy rovnice

  \[\hat{H_0}\psi_n=E_n\psi_n.\]

  Porušenému hamiltoniánu však nepřísluší žádné stacionární stavy, a proto budeme studovat pouze přechody mezi stacionárními stavy neporušeného hamiltoniánu, které porucha vyvolala.

  Uvažujme, že porucha působí pouze v časovém intervalu \(0< t<\tau\), proto před zapnutím a po vypnutí poruchy je \(\lambda\hat{W}(t)=0\) a \(\hat{H}(t)=\hat{H_0}\). Náchází-li se systém v nějakém stacionárním stavu před zapnutím poruchy, může vlivem poruchy dojít k přechodu do stavu jiného, ve kterém systém po vypnutí poruchy již setrvá.

  Abychom určili změny systému v celé časové škále, je nutné řešit nestacionární Schrödingerovu rovnici, jejiž obecné řešení má tvar

  \[\psi(\vec{r},t)=\sum_n {c_n(t)\psi_n(\vec{r})e^{−i\frac{E_n}{\hbar}t}}.\]

  Kontrétní řešení obdržíme volbou počátečních podmínek a výpočtem časově závislých koeficientů \(c_n(t)\). Jako počáteční podmínku volíme, že se systém nacházel v okamžiku zapnutí poruchy v p-tém stavu

  \[\psi^{(p)}(\vec{r},t=0)=\psi_p.\]

  Tato podmínka vede ke konkrétnímu řešení

  \[\psi^{(p)}(\vec{r},t)=\sum_n {c_n^{(p)}(t)\psi_n(\vec{r})e^{−i\frac{E_n}{\hbar}t}}.\]

  Počáteční hodnoty koeficientů \(c_n^{(p)}(t)\) určíme z počáteční podmínky

  \[\psi^{(p)}(\vec{r},t=0)=\sum_n c_n^{(p)}(t)\psi_n(\vec{r})=\psi_n,\]

  tedy

  \[c_n^{(p)}(t=0)=\delta_{np}.\]

  Vypočítáme-li všechny koeficienty \(c_n^{(p)}(t)\), můžeme poté určit veličinu

  \[P_{p\rightarrow k}=\left|c_k^{(p)}(t=\tau)\right|^2,\]

  kterou můžeme rozumět pravděpodobnost, že se systém nachází ve stavu \(k\) v okamžiku vypnutí poruchy a tedy pravděpodobnost přechodu ze stavu \(p\) do stavu \(k\). Některé pravděpodobnosti přechodu mohou být nulové, takovým přechodům se říká zakázané. Opakem jsou přechody dovolené. Jejich souhrn tvoří výběrová pravidla.

  Vypočítejme nyní koeficienty \(c_n^{(p)}(t)\) dosazením konkrétního tvaru vlnových funckí \(\psi^{(p)}\) do nestacionární Schrödingerovy rovnice

  \[i\hbar\frac{\partial }{\partial t}\psi^{(p)}=i\hbar\frac{\partial }{\partial t}\sum_n {c_n^{(p)}(t)\psi_n(\vec{r})e^{−i\frac{E_n}{\hbar}t}}=\] \[=i\hbar\sum_n c_n^{(p)}(t)\psi_n(\vec{r})\left(−i\frac{E_n}{\hbar}\right)e^{−i\frac{E_n}{\hbar}}t+i\hbar\sum_n {\frac{\mathrm{d} }{\mathrm{d} t}\left(c_n^{(p)}(t)\right)\psi_n(\vec{r})e^{−i\frac{E_n}{\hbar}t}}=\] \[=H_0\sum_n {c_n^{(p)}(t)\psi_n(\vec{r})e^{−i\frac{E_n}{\hbar}t}}+\lambda\hat{W}(t)\sum_n {c_n^{(p)}(t)\psi_n(\vec{r})e^{−i\frac{E_n}{\hbar}t}}.\]

  První členy na druhém a třetím řádku se díky neporušené stacionární Schrödingerovy rovnice rovnají. Upravená rovnost tedy je

  \[i\hbar\sum_n {\frac{\mathrm{d} }{\mathrm{d} t}\left(c_n^{(p)}(t)\right)\psi_n(\vec{r})e^{−i\frac{E_n}{\hbar}t}}=\lambda\hat{W}(t)\sum_n {c_n^{(p)}(t)\psi_ne^{−i\frac{E_n}{\hbar}t}}.\]

  Skalárně tuto rovnost vynásobíme zleva výrazem \(\psi_k e^{−i\frac{E_k}{\hbar}t}\) a využijeme ortonormality

  \[i\hbar \frac{\mathrm{d} }{\mathrm{d} t} c_k^{(p)}(t)=\sum_n \left\langle\psi_k|\lambda\hat{W}(t)\psi_n\right\rangle c_n^{(p)}(t)e^{i\frac{E_k−E_n}{\hbar}t}.\]

  Tuto soustavu diferenciálních rovnic je možno řešit až po zadání přesného tvaru poruchy a obvykle je to značně obtížný úkol. Je-li porucha dostatečně malá (je-li \(\lambda\) dostatečně malé), můžeme brát koeficienty \(c_n^{(p)}\) vzít jako jejich nulté přiblížení, tedy známé počáteční hodnoty \(c_n^{(p)}(t)\doteq c_n^{(p)}(t=0)=\delta_{np}\) dosadit do pravé strany rovnice. Tím se diferenciální rovnice zjednodušší na

  \[i\hbar \frac{\mathrm{d} }{\mathrm{d} t} c_k^{(p)}(t)=\left\langle\psi_k|\lambda\hat{W}(t)\psi_p\right\rangle e^{i\frac{E_k−E_p}{\hbar}t}.\]

  Zajímáme-li se pouze o přechody, je \(k\neq p\).

  Koeficient \(c_k^{(p)}(t)\) tedy určíme z výrazu

  \[c_k^{(p)}(t)=\frac{1}{i\hbar}\int_{0}^{\tau}\left\langle\psi_k|\hat{V}(t)\psi_p\right\rangle e^{i\frac{E_k−E_p}{\hbar}t}\, \mathrm{d}t.\]

  Jedná se o vztah pro koeficient přechodu \(c_k^{(p)}(t)\) v prvním řádu poruchové teorie.

• Řešení

  Zajímá nás pravděpodobnost přechodu systému vlivem poruchy do vlastního stavu \(\psi_f\). Spočítejme proto koeficient \(c_f^{(p)}(t)\), který stojí před vlastním stavem \(\psi_f\) v lineární kombinaci konečného stavu systému při vypnutí poruchy.

  Proto nyní dosadíme do vzorce

  \[c_f^{(p)}(\tau)=\frac{1}{i\hbar}\int_{0}^{\tau}\left\langle\psi_f\bigg|\hat{V}(t)\psi_i\right\rangle e^{i\frac{E_f−E_i}{\hbar}t}\, \mathrm{d}t.\]

  Označme

  \[\frac{E_f−E_i}{\hbar}=\omega_{fi},\] \[\left\langle\psi_f\bigg|\hat{V}(t)\psi_i\right\rangle=V_{fi}(t),\]

  kde \(V_{fi}(t)\) obecně závisí na čase, ale v této úloze, kde uvažujeme konstantní poruchu (která je pouze zapnuta v určitém čase) se jedná o konstantu.

  Tedy

  \[c_f^{(p)}(\tau)=\frac{1}{i\hbar}\int_{0}^{\tau}V_{fi} e^{i\omega_{fi}t}\, \mathrm{d}t=\frac{1}{i\hbar}V_{fi}\left[\frac{e^{i\omega_{fi}t}}{i\omega_{fi}}\right]_0^\tau=\frac{−1}{\hbar\omega_{fi}}V_{fi}\left(e^{i\omega_{fi}t}−1\right)=\frac{V_{fi}}{E_f−E_i}\left(1−e^{i\omega_{fi}t}\right).\]

  Z toho určíme pravděpodobnost přechodu jako

  \[P_{p\rightarrow k}=\left|c_f^{(p)}(\tau)\right|^2=\left|\frac{V_{fi}}{E_f−E_i}\right|^2\left|1−e^{i\omega_{fi}\tau}\right|^2=\] \[=\left|\frac{V_{fi}}{E_f−E_i}\right|^2\left[1−\mathrm{cos}(\omega_{fi}\tau)−i\mathrm{sin}(\omega_{fi}\tau)\right]\left[1−\mathrm{cos}(\omega_{fi}\tau)+i\mathrm{sin}(\omega_{fi}\tau)\right]=\] \[=\left|\frac{V_{fi}}{E_f−E_i}\right|^2\left[\left(1−\mathrm{cos}(\omega_{fi}\tau)\right)^2+\mathrm{sin}^2(\omega_{fi}\tau)\right]=\left|\frac{V_{fi}}{E_f−E_i}\right|^2(1−2\mathrm{cos}(\omega_{fi}\tau)+1)=\left|\frac{V_{fi}}{E_f−E_i}\right|^2 4\mathrm{sin}^2\left(\frac{\omega_{fi}\tau}{2}\right)=\] \[=\frac{\left|V_{fi}\right|^2}{\hbar^2} \frac{\mathrm{sin}^2\left(\frac{\omega_{fi}\tau}{2}\right)}{\left(\frac{\omega_{fi}}{2}\right)^2}.\]

  Tato závislost na \(\omega_{fi}\) je znázorněna v následujícím grafu.

  

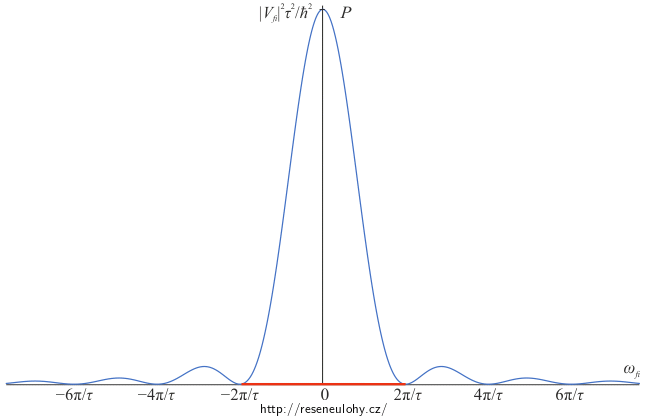
  Pro \(\omega_{fi}\rightarrow0\) je pravděpodobnost přechodu \(\frac{\left|V_{fi}\right|^2}{\hbar^2}\tau^2\). Pro \(\omega_{fi}\rightarrow\infty\) je pravděpodobnost přechodu \(0\). Pravděpodobnost přechodu je dále nulová, když

  \[\mathrm{sin}^2\left(\frac{\omega_{fi}\tau}{2}\right)=0\Rightarrow \omega_{fi}=\frac{2\pi k}{\tau},\,k\in\mathbb{Z}.\]

  Nezanedbatelná pravděpodobnost přechodu je určena podmínkou (a v grafu vyznačena červeně)

  \[\frac{−2\pi}{\tau}\leq\omega_{fi}\leq \frac{2\pi}{\tau},\]

  jinak také

  \[|\omega_{fi}|\leq \frac{2\pi}{\tau}.\]

  Z toho

  \[\left|\frac{E_f−E_i}{\hbar}\right|\leq \frac{2\pi}{\tau},\] \[\left|\frac{\Delta E}{\hbar}\right|\leq \frac{2\pi}{\tau},\] \[\tau|\Delta E|\leq 2\pi\hbar.\]

  Poslední výraz znamená, že systém může přejít vlivem poruchy pouze do stavů, které mají rozdílnou energii oproti původnímu stavu o hodnotu

  \[|\Delta E|\leq2\frac{\pi\hbar}{\tau}.\]

  Vidíme, že čím kratší je působení poruchy, tím může dojít k větší změně energie původního stavu. A naopak, pokud chceme, aby se energie moc neměnila, pak je třeba, aby porucha působila po dlouhou dobu.

• Odpověď

  Uvažujeme-li systém nacházející se ve vlastním stavu \(\psi_i\) neporušeného hamiltoniánu \(\hat{H}_0\) v čase \(t=0\) a poruchu

  \[\hat{V}(t)=0,\, t< 0,\,\tau< t, \] \[\hat{V}(t)=\hat{V},\, \tau>t>0,\]

  tj. poruchu, která je na intervalu \((0,\,\tau)\) konstantní a „zapneme“ ji v čase \(t=0\), pak pravděpodobnost přechodu systému v časovém intervalu \((0,\tau)\) z počátečního stavu do stavu \(\psi_f\) je

  \[P_{p\rightarrow k}=\left|c_f^{(p)}(\tau)\right|^2=\frac{\left|V_{fi}\right|^2}{\hbar^2} \frac{\mathrm{sin}^2\left(\frac{\omega_{fi}\tau}{2}\right)}{\left(\frac{\omega_{fi}}{2}\right)^2},\]

  kde

  \[\left\langle\psi_f\Big|\hat{V}(t)\psi_i\right\rangle=V_{fi}(t),\] \[\frac{E_f−E_i}{\hbar}=\omega_{fi}.\]

  Větší hodnoty pravděpodobnosti přechodu nabývají za podmínky

  \[\tau|\Delta E|\leq2\pi\hbar,\]

  jinak jsou prakticky nulové. To znamená, že systém může přejít vlivem poruchy pouze do stavů, které mají rozdílnou energii oproti původnímu stavu o hodnotu

  \[|\Delta E|\leq2\frac{\pi\hbar}{\tau}.\]