Sbírka řešených úloh

Síla na stěnu pravoúhlé jámy

Úloha číslo: 713

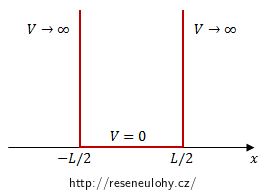
Elektron je vázán uvnitř nekonečně hluboké pravoúhlé potenciálové jámy šířky L

s neprostupnými stěnami: potenciál V(x) = 0 pro |x| ≤ L/2 a V(x) → ∞ pro |x| > L/2.

Elektron se nachází v základním stavu, který je popsán normovanou vlnovou funkcí

\[\psi_1(x)=\sqrt{\frac{2}{L}}\,\cos\left(\frac{\pi x}{L}\right)\,,\]

a přísluší mu energie \(E_1=\frac{\pi^2 \hbar^2}{2m_e L^2}\). Určete sílu působící na stěnu jámy nejprve obecně a pak pro konkrétní jámu šířky L = 10⁻¹⁰ m (tj. řádově rozměr atomu).

• Nápověda – síla

  Jak souvisí síla, kterou částice působí na stěnu jámy, s její energií?

• Řešení nápovědy – síla

  Pokud se v systému neztrácí energie jinak než deformací (změnou šířky) jámy, platí, že zapůsobí-li částice zevnitř silou na stěnu jámy a posune ji tím o δL (rozšíří), vykoná práci F·δL rovnou úbytku její energie, tedy F·δL = E₁(L) − E₁(L+δL). Odtud

  \[F=-\frac{E_1(L+\delta L)-E_1(L)}{\delta L}\,,\]

  resp. v limitním případě (neboť jáma se ve skutečnosti nezvětšuje)

  \[F=-\frac{\partial E_1}{\partial L}\,.\]

  Síla, kterou částice tlačí na stěnu jámy, souvisí s tím, jak by se měnila její energie při měnící se šířce jámy.

• Řešení

  Elektronu v základním stavu přísluší energie \(E_1=\frac{\pi^2 \hbar^2}{2m_e L^2}\). Síla, kterou elektron působí na stěnu jámy, proto bude mít velikost

  \[F=-\frac{\partial E_1}{\partial L}=\frac{\pi^2 \hbar^2}{m_e L^3}\,.\]

  Pro konkrétní jámu šířky L = 10⁻¹⁰ m vychází

  \[F=\frac{\pi^2\,\cdot\,\left(1{,}055\,\cdot\,10^{-34}\right)^2}{9{,}11\,\cdot\,10^{-31}\,\cdot\,\left(10^{-10}\right)^3}\ \mbox{N}=\frac{\pi^2\,\cdot\,1{,}055^2}{9{,}11}\,10^{-7}\ \mbox{N}\,\dot{=}\, 1{,}2\,\cdot\,10^{-7}\ \mbox{N}\,.\]

• Odpověď

  Průměrná síla působící na stěnu nekonečně hluboké pravoúhlé potenciálové jámy šířky L, vyvolaná přítomností elektronu v základním stavu uvnitř této jámy, je rovna \(F=\frac{\pi^2 \hbar^2}{m_e L^3}\), pro konkrétní jámu šířky L = 10⁻¹⁰ m pak přibližně 10⁻⁷ N.

• Odkaz

  Srovnej s úlohou Tlak na stěnu sférické jámy této sbírky.