Návazné SG experimenty
Úloha číslo: 4358
Pomocí Sternova–Gerlachova zařízení natočeného ve směru \(z\) vybereme z původně nepolarizovaného svazku pouze elektrony, které mají kladný průmět spinu do osy \(z\). Tento svazek necháme projít dalším Sternovým–Gerlachovým přístrojem natočeným ve směru \(x\). Pokud dojde k rozštěpení svazku, vybereme opět svazek s kladným průmětem spinu. Ten necháme projít Sternovým–Gerlachovým přístrojem natočeným opět ve směru \(z\). Spočtěte poměry, v jakých se štěpí svazky ve všech přístrojích, a vysvětlete rozdíl oproti klasickému chování.
Nápověda 1
Připomeňte si tvar operátorů průmětu spinu \(\frac{1}{2}\) do os \(x\) a \(z\). Vypočtěte nebo vyhledejte jejich vlastní čísla a příslušné vlastní vektory.
Nápověda 2
Připomeňte si nebo vyhledejte, jak je třeba rozložit popis stavu vstupujícího do měření a jak lze z tohoto rozkladu určit pravděpodobnosti naměření jednotlivých hodnot.
Řešení
Jelikož do prvního Sternova–Gerlachova zařízení vstupují elektrony s náhodnou orientací spinu, bude za ním stejná pravděpodobnost naměření obou možných hodnot průmětu spinu do osy \(z\), a sice \(P_+ = P_- = \frac{1}{2}\). Díky tomu rovněž známe vektory, které popisují stav elektronů v obou případech. Vybereme pouze elektrony, které mají průmět spinu do osy \(z\) roven \(+ \frac{\hbar}{2}\). Tomuto vlastnímu číslu přísluší vlastní vektor \(\left |z+ \right \rangle = \begin{pmatrix} 1\\ 0 \end{pmatrix}\).
Svazek elektronů v tomto stavu dále projde Sternovým–Gerlachovým zařízením natočeným ve směru \(x\). Axiom o měření říká, že pokud chceme určit pravděpodobnosti naměření obou možných hodnot, musíme stav, který vstupuje do měření, vyjádřit jako lineární kombinaci vlastních stavů měřené veličiny. Hledáme tedy rozklad
\[ |z+\rangle = c_1 |x+\rangle + c_2 |x-\rangle \, , \]kde \(c_1, c_2\) jsou zatím neznámé komplexní konstanty.
Nyní dosadíme za příslušné vlastní vektory
\[ \begin{pmatrix} 1\\ 0 \end{pmatrix} = c_1 \frac{1}{\sqrt{2}} \begin{pmatrix} 1\\ 1 \end{pmatrix} + c_2 \frac{1}{\sqrt{2}} \begin{pmatrix} -1\\ 1 \end{pmatrix} \, . \]Tuto rovnost si nyní rozepíšeme na rovnosti jednotlivých složek, čímž získáme soustavu dvou lineárních rovnic o dvou neznámých
\[ 1 = \frac{c_1}{\sqrt{2}} - \frac{c_2}{\sqrt{2}} \, , \] \[ 0 = \frac{c_1}{\sqrt{2}} + \frac{c_2}{\sqrt{2}} \, . \]Tyto rovnice nyní sečteme a vyjádříme si koeficient \(c_1\)
\[ 1 = \frac{2c_1}{\sqrt{2}} \,\, \rightarrow \, \, c_1 = \frac{1}{\sqrt{2}} \, . \]Navíc ze druhé rovnice ihned vidíme, že \(c_1 = - c_2\), tedy
\[ c_2 = - \frac{1}{\sqrt{2}} \, . \]Hledaný rozklad má tvar
\[ |z+\rangle = \frac{1}{\sqrt{2}} |x+\rangle - \frac{1}{\sqrt{2}} |x-\rangle \, . \]Pravděpodobnosti naměření jednotlivých hodnot jsou rovny druhé mocnině velikosti příslušného koeficientu, tj.
\[ P_+ = \left |c_1 \right |^2 = \frac{1}{2} \, , \] \[ P_- = \left |c_2 \right |^2 = \frac{1}{2} \, . \]Vidíme, že obě hodnoty mají stejnou pravděpodobnost naměření, dojde tedy k rozštěpení na dva stejně intenzivní svazky. Vybereme svazek s kladným průmětem spinu do směru \(x\) a necháme jej projít Sternovým–Gerlachovým zařízením natočeným opět ve směru \(z\). Analogicky předchozí části rozložíme stav \(|x+\rangle\) vstupující do Sternova–Gerlachova zařízení na
\[ |x+\rangle = d_1 |z+\rangle + d_2 |z-\rangle \, , \]kde \(d_1, d_2\) jsou hledané komplexní konstanty.
Po dosazení vlastních vektorů a rozepsání na jednotlivé složky získáme rovnou
\[ \frac{1}{\sqrt{2}} = d_1 \, , \] \[ \frac{1}{\sqrt{2}} = d_2 \, . \]Hledaný rozklad má tvar
\[ |x+\rangle = \frac{1}{\sqrt{2}} |z+\rangle + \frac{1}{\sqrt{2}} |z-\rangle \, . \]Pravděpodobnosti naměření jednotlivých hodnot jsou vždy rovny druhé mocnině velikosti příslušného koeficientu, tj.
\[ P_+ = \left |d_1 \right |^2 = \frac{1}{2} \, , \] \[ P_- = \left |d_2 \right |^2 = \frac{1}{2} \, . \]Naměření obou možných hodnot průmětu spinu je tedy opět stejně pravděpodobné. Jde o názornou ukázku toho, jak změření hodnoty průmětu spinu do osy \(x\) druhým Sternovým–Gerlachovým zařízením „zničilo informaci“ o průmětu spinu do osy \(z\). To je rozdíl oproti klasickému chování, kde bychom došli k závěru, že když už jsme záporný průmět do osy \(z\) odfiltrovali, neměl by se znovu objevit, protože měření děláme tak, aby průměty spinu neovlivnilo (což v kvantové fyzice není možné).
Výše provedené výpočty zde uvedeme ještě schématicky na obrázku, který byl převzat ze šesté kapitoly skript Kvantová fyzika (nejen) pro budoucí učitele k předmětu Úvod do kvantové mechaniky a kvantové teorie.
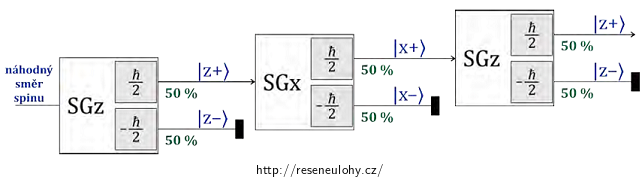
Odpověď
Ve všech přístrojích se svazky štěpí na poloviny, jedna polovina s kladným průmětem spinu a druhá polovina se záporným průmětem spinu.
Oproti klasickému chování, kde bychom neočekávali opětovný výskyt záporného průmětu spinu do osy \(z\), zde díky tomu, že měření ovlivní stav elektronu, tento průmět naměříme.
Komentář – výpočet koeficientů rozkladu pomocí skalárního součinu
Hledané koeficienty \(c_1, \, c_2\) rozkladu
\[ |z+\rangle = c_1 |x+\rangle + c_2 |x-\rangle \]můžeme určit pomocí skalárního součinu
\[ c_1 = \langle x+ | z+ \rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \frac{1}{\sqrt{2}} \, , \] \[ c_2 = \langle x- | z+ \rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} -1 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = - \frac{1}{\sqrt{2}} \, . \]Analogicky postupujeme při hledání koeficientů \(d_1, \, d_2\) rozkladu
\[ |x+\rangle = d_1 |z+\rangle + d_2 |z-\rangle \, . \]S využitím skalárního součinu určíme koeficienty
\[ d_1 = \langle z+ | x+ \rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \frac{1}{\sqrt{2}} \, , \] \[ d_2 = \langle z- | x+ \rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 0 & 1 \end{pmatrix} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \frac{1}{\sqrt{2}} \, . \]Oba postupy, jak s využitím soustavy dvou lineárních rovnic o dvou neznámých, tak s využitím skalárního součinu, jsou korektní a dávají stejné výsledky.


