Sbírka řešených úloh

Střední hodnoty operátorů a Heisenbergova relace neurčitosti

Úloha číslo: 2012

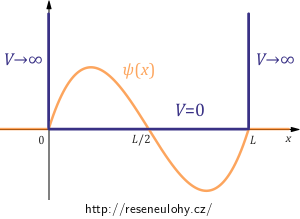
Najděte normalizační konstantu \(A\) a střední hodnoty operátorů \(\hat{x}\), \(\hat{x}^2\), \(\hat{p}\), \(\hat{p}^2\) ve stavu popsaném vlnovou funkcí \[\psi(x)= \begin{cases} Ax\left(\frac{L}{2}-x\right)(L-x) & \quad \text{pro } x\in (0,L), \\ 0 & \quad \text{jinak},\\ \end{cases}\] kde \(L\) je pevně dané reálné číslo.

Ověřte Heisenbergovu relaci neurčitosti v tomto stavu.

Poznámka: Jedná se o vlnovou funkci popisující stav částice v nekonečně hluboké jámě šířky L.

• Nápověda 1

  Uvědomte si, jak se normuje vlnová funkce a jak se vypočítá střední hodnota operátoru.

  Připomeňte si, jak se definují operátory souřadnic a hybnosti.

• Řešení nápovědy 1

  Chceme-li normovat vlnovou funkci \(\varphi\), potřebujeme najít normalizační konstantu \(A\), která je obecně komplexní číslo. Vynásobíme-li normalizační konstantou \(A\) nenormovanou vlnovou funkci \(\varphi\), získáme normovanou vlnovou funkci \(\psi\) \[\psi=A\varphi.\] Při hledání normalizační konstanty \(A\) vyjdeme z definice normované vlnové funkce, pro kterou platí normovací podmínka \[(\psi, \psi)=1.\] Konstanta \(A\) tedy musí splňovat \[1=(\psi, \psi)=\int_{-\infty}^\infty{\psi^\ast\psi}\,\mathrm{d}x=\int_{-\infty}^\infty{A^\ast\varphi^\ast A\varphi}\,\mathrm{d}x=A^\ast A\int_{-\infty}^\infty{\varphi^\ast \varphi}\,\mathrm{d}x=|A|^2\int_{-\infty}^\infty{\varphi^\ast\varphi}\,\mathrm{d}x,\] odtud vyjádříme velikost normalizační konstanty \(|A|\) \[|A|=\sqrt{\frac{1}{\int_{-\infty}^\infty{\varphi^\ast\varphi}\,\mathrm{d}x}}.\] Normalizační konstanta \(A\) však není určena jednoznačně, zjistili jsme pouze její velikost. Z důvodu zjednodušení výpočtů se obvykle normalizační konstanta \(A\) volí reálná kladná.

   

  Střední hodnota operátoru \(\hat{O}\) ve stavu \(\varphi\) je definována \[\langle \hat{O}\rangle_\varphi=\frac{(\varphi, \hat{O}\varphi)}{(\varphi, \varphi)}=\frac{\int_{-\infty}^\infty{\varphi^\ast O\varphi}\,\mathrm{d}x}{\int_{-\infty}^\infty{\varphi^\ast \varphi}\,\mathrm{d}x}.\] Střední hodnota operátoru \(\hat{O}\) pro normovanou vlnovou funkci \(\psi\) se vypočte jako \[\langle \hat{O}\rangle_\psi=\frac{(\psi, \hat{O}\psi)}{(\psi, \psi)}=\frac{(\psi, \hat{O}\psi)}{1}=(\psi, \hat{O}\psi)=\int_{-\infty}^\infty{\psi^\ast \hat{O}\psi}\,\mathrm{d}x.\]

   

  Zopakujme si ještě, jak se definuje operátor souřadnice \(\hat{x}\) \[\hat{x}=x\hat{1}\] a operátor hybnosti \(\hat{p}\) \[\hat{p}=-i\hbar\frac{\mathrm{d}}{\mathrm{d}x}.\] Vyjádříme si také druhé mocniny těchto operátorů \[\hat{x}^2=\left(x\hat{1}\right)^2=x^2\hat{1}^2=x^2\hat{1},\] \[\hat{p}^2=\left(-i\hbar\frac{\mathrm{d}}{\mathrm{d}x}\right)^2=\left(-i\hbar\right)^2\left(\frac{\mathrm{d}}{\mathrm{d}x}\right)^2=-\hbar^2\frac{\mathrm{d}^2}{\mathrm{d}x^2}.\]

• Nápověda 2

  Vyhledejte si znění Heisenbergovy relace neurčitosti a zamyslete se, co je třeba vypočítat při jejím ověřování.

• Řešení nápovědy 2

  Heisenbergova relace neurčitosti je vyjádřena vztahem \[\Delta x\Delta p\geq \frac{\hbar}{2},\] kde \(\Delta x\) je neurčitost určení polohy a \(\Delta p\) neurčitost určení hybnosti. Heisenbergova relace neurčitosti tvrdí, že je principiálně nemožné současně přesně změřit polohu i hybnost částice, proto se v kvantové mechanice musíme vzdát pojmu trajektorie částice.

  Ověřit Heisenbergovu relaci neurčitosti znamená porovnat součin neurčitosti určení polohy a neurčitosti určení hybnosti \(\Delta x\Delta p\) s \(\frac{\hbar}{2}.\)

   

  Neurčitost určení polohy \(\Delta x\) zavedeme jako druhou odmocninu ze střední kvadratické odchylky od střední hodnoty polohy \(\hat{x}-\left\langle \hat{x}\right\rangle\) \[\Delta x=\sqrt{\left\langle(\hat{x}-\left\langle \hat{x}\right\rangle)^2\right\rangle}.\] Neurčitost určení polohy plní funkci měřítka velikosti chyb při měření polohy. Ukazuje nám, jak moc se poloha může lišit od střední hodnoty polohy.

  Střední kvadratickou odchylku polohy upravíme \[\left\langle(\hat{x}-\left\langle \hat{x}\right\rangle)^2\right\rangle=\left\langle \hat{x}^2-2\hat{x}\left\langle \hat{x}\right\rangle+\left\langle \hat{x}\right\rangle^2\right\rangle=\left\langle \hat{x}^2\right\rangle-2\left\langle \hat{x}\right\rangle^2+\left\langle \hat{x}\right\rangle^2=\left\langle \hat{x}^2\right\rangle-\left\langle \hat{x}\right\rangle^2\] a dosadíme do vzorce pro výpočet neurčitosti určení polohy \(\Delta x\) \[\Delta x=\sqrt{\left\langle(\hat{x}-\left\langle \hat{x}\right\rangle)^2\right\rangle}=\sqrt{\left\langle \hat{x}^2\right\rangle-\left\langle \hat{x}\right\rangle^2},\] kde \(\left\langle \hat{x}^2\right\rangle\) a \(\left\langle \hat{x}\right\rangle\) jsou střední hodnoty operátorů polohy.

   

  Při vyjádření vztahu pro neurčitost určení hybnosti \(\Delta p\) budeme postupovat analogicky. Neurčitost určení hybnosti \(\Delta p\) vystihuje, jak moc se může lišit hybnost od střední hodnoty hybnosti.

  Upravenou střední kvadratickou odchylku hybnosti \[\left\langle(\hat{p}-\left\langle \hat{p}\right\rangle)^2\right\rangle=\left\langle \hat{p}^2-2\hat{p}\left\langle \hat{p}\right\rangle+\left\langle \hat{p}\right\rangle^2\right\rangle=\left\langle \hat{p}^2\right\rangle-2\left\langle \hat{p}\right\rangle^2+\left\langle \hat{p}\right\rangle^2=\left\langle \hat{p}^2\right\rangle-\left\langle \hat{p}\right\rangle^2\] dosadíme do vzorce pro výpočet neurčitosti určení hybnosti \(\Delta p\) \[\Delta p=\sqrt{\left\langle(\hat{p}-\left\langle \hat{p}\right\rangle)^2\right\rangle}=\sqrt{\left\langle \hat{p}^2\right\rangle-\left\langle \hat{p}\right\rangle^2},\] kde \(\left\langle \hat{p}^2\right\rangle\) a \(\left\langle \hat{p}\right\rangle\) jsou střední hodnoty operátorů hybnosti.

• Řešení

  Budeme zkoumat vlnovou funkci popisující stav částice v nekonečně hluboké jámě šířky \(L\) \[ \psi(x)= \begin{cases} Ax\left(\frac{L}{2}-x\right)(L-x) & \quad \text{pro } x\in (0,L),\\ 0 & \quad \text{jinak,}\\ \end{cases}\] kde \(L\) je reálné číslo.

  Normalizační konstantu \(A\) vypočteme z normovací podmínky,

  \[1=(\psi, \psi)=\int_{-\infty}^\infty{\psi^\ast\psi}\,\mathrm{d}x=\]

  do které dosadíme zadanou funkci \(\psi\).

  \[=\int_{-\infty}^0{0{\cdot}0}\,\mathrm{d}x+\int_0^L{A^\ast x\left(\frac{L}{2}-x\right)(L-x)Ax\left(\frac{L}{2}-x\right)(L-x)}\,\mathrm{d}x+\int_L^\infty{0{\cdot}0}\,\mathrm{d}x=\]

  První a poslední integrál je nulový. Vytkneme konstantu před integrál, dosadíme hodnotu integrálu (viz oddíl Výpočet integrálů níže) a upravíme.

  \[=0+|A|^2\int_0^L{x^2\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x+0=|A|^2\frac{L^7}{840}=\frac{|A|^2L^7}{840}\]

  Z rovnice \(1=\frac{|A|^2L^7}{840}\) vyjádříme velikost normalizační konstanty \[\left |A\right\vert=\sqrt{\frac{840}{L^7}}.\]

  Nyní máme normovanou vlnovou funkci \[ \psi(x)= \begin{cases} \sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x) & \quad \text{pro } x\in (0,L),\\ 0 & \quad \text{jinak,}\\ \end{cases}\] která je nulová pro všechna \(x\) neležící v intervalu \((0, L)\) a pro kterou platí \((\psi, \psi)=1.\)

   

  Střední hodnotu operátoru \(\hat{x}\) pro normovanou vlnovou funkci \(\psi\) vypočteme ze vztahu

  \[\left\langle \hat{x}\right\rangle_\psi=\left(\psi, \hat{x}\psi\right)=\int_{-\infty}^\infty{\psi^\ast x\psi}\,\mathrm{d}x=\]

  dosazením zadané funkce \(\psi\),

  \[=\int_{-\infty}^0{0\cdot x\cdot 0}\,\mathrm{d}x+\int_0^L{\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)x\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)}\,\mathrm{d}x+\int_L^\infty{0\cdot x\cdot 0}\,\mathrm{d}x=\]

  vytkneme konstanty před integrál, dosadíme hodnoty integrálů (viz Výpočet integrálů) a upravíme.

  \[=0+\frac{840}{L^7}\int_0^L{x^3\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x+0=\frac{840}{L^7}\frac{L^8}{1680}=\frac{L}{2}\]

  Při výpočtu ostatních středních hodnot budeme postupovat stejně, proto další výpočty středních hodnot operátorů uvedeme stručněji.

   

  Střední hodnota operátoru \(\hat{x}^2\) pro normovanou vlnovou funkci \(\psi\) je

  \[\left\langle \hat{x}^2\right\rangle_\psi=\left(\psi, \hat{x}^2\psi\right)=\int_{-\infty}^\infty{\psi^\ast x^2\psi}\,\mathrm{d}x=\] \[=\int_0^L{\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)x^2\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)}\,\mathrm{d}x=\]

  (nyní integrujeme - viz Výpočet integrálů)

  \[=\frac{840}{L^7}\int_0^L{x^4\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x= \frac{840}{L^7}\frac{L^9}{2520}=\frac{L^2}{3}.\]

   

  Střední hodnota operátoru \(\hat{p}\) pro normovanou vlnovou funkci \(\psi\) je

  \[\left\langle \hat{p}\right\rangle_\psi=(\psi, \hat{p}\psi)=\int_{-\infty}^\infty{\psi^\ast \left(-i\hbar\right)\frac{\mathrm{d}\psi}{\mathrm{d}x}}\,\mathrm{d}x=\] \[=\int_0^L{\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)\left(-i\hbar\right)\frac{\mathrm{d}\left[\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)\right]}{\mathrm{d}x}}\,\mathrm{d}x=\]

  (nejdříve vypočítáme derivaci funkce, až pak můžeme integrovat - viz Výpočet integrálů)

  \[=-i\hbar \frac{840}{L^7}\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\frac{\mathrm{d}\left[x^3-\frac{3L}{2}x^2+\frac{L^2}{2}x\right]}{\mathrm{d}x}}\,\mathrm{d}x=\] \[=-i\hbar \frac{840}{L^7}\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\left(3x^2-3Lx+\frac{L^2}{2}\right)}\,\mathrm{d}x=-i\hbar \frac{840}{L^7}\cdot 0=0.\]

   

  Střední hodnota operátoru \(\hat{p}^2\) pro normovanou vlnovou funkci \(\psi\) je

  \[\left\langle \hat{p}^2\right\rangle_\psi=\left(\psi, \hat{p}^2\psi\right)=\int_{-\infty}^\infty{\psi^\ast \left(-\hbar^2\right)\frac{\mathrm{d}^2\psi}{\mathrm{d}x^2}}\,\mathrm{d}x=\] \[=\int_0^L{\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)\left(-\hbar^2\right)\frac{\mathrm{d}^2\left[\sqrt{\frac{840}{L^7}}x\left(\frac{L}{2}-x\right)(L-x)\right]}{\mathrm{d}x^2}}\,\mathrm{d}x=\]

  (spočítáme druhou derivaci funkce a poté integrujeme - viz Výpočet integrálů)

  \[=-\hbar^2 \frac{840}{L^7}\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\frac{\mathrm{d}^2\left[x^3-\frac{3L}{2}x^2+\frac{L^2}{2}x\right]}{\mathrm{d}x^2}}\,\mathrm{d}x=\] \[=-\hbar^2 \frac{840}{L^7}\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\frac{\mathrm{d}\left[3x^2-3Lx+\frac{L^2}{2}\right]}{\mathrm{d}x}}\,\mathrm{d}x=\] \[=-\hbar^2 \frac{840}{L^7}\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)(6x-3L)}\,\mathrm{d}x=-\hbar^2 \frac{840}{L^7}\left(-\frac{L^5}{20}\right)=\frac{42\hbar^2}{L^2}.\]

   

  Dále chceme ověřit, že je ve stavu \(\psi\) splněna Heisenbergova relace neurčitosti \[\Delta x\Delta p\geq \frac{\hbar}{2}.\]

  Nejdříve do vzorce pro neurčitost určení polohy \(\Delta x\) dosadíme zjištěné střední hodnoty polohy \(\left\langle \hat{x}^2\right\rangle_\psi=\frac{L^2}{3}\), \(\left\langle \hat{x}\right\rangle_\psi=\frac{L}{2}\) a vypočteme neurčitost určení polohy \(\Delta x\) \[\Delta x=\sqrt{\left\langle\left(\hat{x}-\left\langle \hat{x}\right\rangle_\psi\right)^2\right\rangle_\psi}=\sqrt{\left\langle \hat{x}^2\right\rangle_\psi-\left\langle \hat{x}\right\rangle_\psi^2}=\sqrt{\frac{L^2}{3}-\left(\frac{L}{2}\right)^2}=\sqrt{\frac{L^2}{12}}.\] Pak analogicky určíme neurčitost určení hybnosti \(\Delta p\). Dříve vypočtené střední hodnoty hybnosti \(\left\langle \hat{p}^2\right\rangle_\psi=\frac{42\hbar^2}{L^2}\) a \(\left\langle \hat{p}\right\rangle_\psi=0\) dosadíme do vzorce pro výpočet neurčitosti určení hybnosti \(\Delta p\) \[\Delta p=\sqrt{\left\langle\left(\hat{p}-\left\langle \hat{p}\right\rangle_\psi\right)^2\right\rangle_\psi}=\sqrt{\left\langle \hat{p}^2\right\rangle_\psi-\left\langle \hat{p}\right\rangle_\psi^2}=\sqrt{\frac{42\hbar^2}{L^2}-0^2}=\sqrt{\frac{42\hbar^2}{L^2}}.\]

  Nyní porovnáme součin neurčitosti určení polohy \(\Delta x\) a neurčitosti určení hybnosti \(\Delta p\) s výrazem \(\frac{\hbar}{2}\)

  \[\Delta x\Delta p=\sqrt{\frac{L^2}{12}}\sqrt{\frac{42\hbar^2}{L^2}}=\sqrt{\frac{L^242\hbar^2}{12L^2}}=\sqrt{\frac{14\hbar^2}{4}}=\sqrt{14}\frac{\hbar}{2}>\frac{\hbar}{2}.\]

  Ověřili jsme, že součin neurčitosti určení polohy a neurčitosti určení hybnosti je větší než \(\frac{\hbar}{2}\). Heisenbergova relace neurčitosti je ve stavu popsaném vlnovou funkcí \(\psi\) splněna.

• Výpočet integrálů

  Při výpočtu všech integrálů v této úloze budeme postupovat stejně. Nejdříve funkci roznásobením upravíme na polynom, pak integrujeme pomocí základního integrálu \[\int{x^n}\,\mathrm{d}x=\frac{1}{n+1}x^{n+1}+c,\] kde \(n\) je přirozené číslo a \(c\) je konstanta. Nakonec vypočteme hodnotu integrálu dosazením integračních mezí a upravíme.

   

  Výpočet normalizační konstanty

  \[\int_0^L{x^2\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x= \int_0^L{\left(x^6-3Lx^5+\frac{13L^2}{4}x^4-\frac{3L^3}{2}x^3+\frac{L^4}{4}x^2\right)}\,\mathrm{d}x=\] \[=\left[\frac{1}{7}x^7-\frac{3L}{6}x^6+\frac{13L^2}{20}x^5-\frac{3L^3}{8}x^4+\frac{L^4}{12}x^3\right]_0^L=\left(\frac{1}{7}-\frac{3}{6}+\frac{13}{20}-\frac{3}{8}+\frac{1}{12}\right)L^7=\frac{L^7}{840}\]

   

  Výpočet střední hodnoty \(\hat{x}\)

  \[\int_0^L{x^3\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x=\int_0^L{\left(x^7-3Lx^6+\frac{13L^2}{4}x^5-\frac{3L^3}{2}x^4+\frac{L^4}{4}x^3\right)}\,\mathrm{d}x=\] \[=\left[\frac{1}{8}x^8-\frac{3L}{7}x^7+\frac{13L^2}{24}x^6-\frac{3L^3}{10}x^5+\frac{L^4}{16}x^4\right]_0^L=\left(\frac{1}{8}-\frac{3}{7}+\frac{13}{24}-\frac{3}{10}+\frac{1}{16}\right)L^8=\frac{L^8}{1680}\]

   

  Výpočet střední hodnoty \(\hat{x}^2\)

  \[\int_0^L{x^4\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x=\int_0^L{\left(x^8-3Lx^7+\frac{13L^2}{4}x^6-\frac{3L^3}{2}x^5+\frac{L^4}{4}x^4\right)}\,\mathrm{d}x=\] \[=\left[\frac{1}{9}x^9-\frac{3L}{8}x^8+\frac{13L^2}{28}x^7-\frac{3L^3}{12}x^6+\frac{L^4}{20}x^5\right]_0^L=\left(\frac{1}{9}-\frac{3}{8}+\frac{13}{28}-\frac{3}{12}+\frac{1}{20}\right)L^8=\frac{L^9}{2520}\]

   

  Výpočet střední hodnoty \(\hat{p}\)

  \[\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\left(3x^2-3Lx+\frac{L^2}{2}\right)}\,\mathrm{d}x=\int_0^L{\left(3x^5-\frac{15L}{2}x^4+\frac{13L^2}{2}x^3-\frac{9L^3}{4}x^2+\frac{L^4}{4}x\right)}\,\mathrm{d}x=\] \[=\left[\frac{3}{6}x^6-\frac{15L}{10}x^5+\frac{13L^2}{8}x^4-\frac{9L^3}{12}x^3+\frac{L^4}{8}x^2\right]_0^L=\left(\frac{1}{2}-\frac{3}{2}+\frac{13}{8}-\frac{3}{4}+\frac{1}{8}\right)L^8=0\]

   

  Výpočet střední hodnoty \(\hat{p}^2\)

  \[\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\left(6x-3L\right)}\,\mathrm{d}x=\int_0^L{\left(6x^4-12Lx^3+\frac{15L^2}{2}x^2-\frac{3L^3}{2}x\right)}\,\mathrm{d}x=\] \[=\left[\frac{6}{5}x^5-\frac{12L}{4}x^4+\frac{15L^2}{6}x^3-\frac{3L^3}{4}x^2\right]_0^L=\left(\frac{6}{5}-\frac{12}{4}+\frac{15}{6}-\frac{3}{4}\right)L^5=-\frac{L^5}{20}\]

   

  Nyní popíšeme, jak lze integrály z této úlohy spočítat v rozhraní WolframAlpha.

  Výpočet normalizační konstanty

  Do řádku pro výpočet se zapíše integrál \(\int_0^L{x^2\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x\) ve tvaru

  integrate x^2 *(L/2-x)^2 *(L-x)^2 dx from x=0 to L,

  klikne se na tlačítko = (compute) a zobrazí se vypočtená hodnota integrálu

  \[\int_0^L{x^2\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x=\frac{L^7}{840}.\]

   

  Výpočet střední hodnoty \(\hat{x}\)

  Intergrál \(\int_0^L{x^3\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x\) byl napsán ve tvaru

  integrate x^3 *(L/2-x)^2 *(L-x)^2 dx from x=0 to L,

  po výpočtu je hodnota integrálu

  \[\int_0^L{x^3\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x=\frac{L^8}{1680}.\]

   

  Výpočet střední hodnoty \(\hat{x}^2\)

  Intergrál \(\int_0^L{x^4\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x\) byl napsán ve tvaru

  integrate x^4 *(L/2-x)^2 *(L-x)^2 dx from x=0 to L,

  po výpočtu je hodnota integrálu

  \[\int_0^L{x^4\left(\frac{L}{2}-x\right)^2(L-x)^2}\,\mathrm{d}x=\frac{L^9}{2520}.\]

   

  Výpočet střední hodnoty \(\hat{p}\)

  Intergrál \(\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\left(3x^2-3Lx+\frac{L^2}{2}\right)}\,\mathrm{d}x\) byl napsán ve tvaru

  integrate x*(L/2-x)*(L-x)*(3*x^2-3*L*x+L^2/2) dx from x=0 to L,

  po výpočtu je hodnota integrálu

  \[\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\left(3x^2-3Lx+\frac{L^2}{2}\right)}\,\mathrm{d}x=0.\]

   

  Výpočet střední hodnoty \(\hat{p}^2\)

  Intergrál \(\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\left(6x-3L\right)}\,\mathrm{d}x\) byl napsán ve tvaru

  integrate x*(L/2-x)*(L-x)*(6*x-3*L) dx from x=0 to L,

  po výpočtu je hodnota integrálu

  \[\int_0^L{x\left(\frac{L}{2}-x\right)(L-x)\left(6x-3L\right)}\,\mathrm{d}x=-\frac{L^5}{20}.\]

• Komentář

  Posuneme-li souřadnici x o \(L/2\), bude vlnová funkce \(\psi_1\) v těchto „nových souřadnicích“ lichou funkcí \[\psi_1(x)=\psi\left(x+\frac{L}{2}\right)= \begin{cases} A\left(x+\frac{L}{2}\right)\left(-x\right)(\frac{L}{2}-x) & \quad \text{pro } x\in \left(-\frac{L}{2},\frac{L}{2}\right), \\ 0 & \quad \text{jinak},\\ \end{cases}\] kde \(L\) je pevně dané reálné číslo.

  

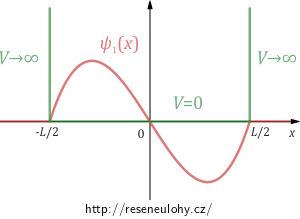
  Využitím vlastností sudých a lichých funkcí si můžeme zjednodušit výpočet integrálů. Integrál z liché funkce na symetrickém intervalu okolo počátku je nulový. Integrál ze sudé funkce na symetrickém intervalu okolo počátku můžeme počítat jako dvojnásobek integrálu počítaného přes pravou polovinu intervalu.

   

  Nyní snadno vypočteme střední hodnotu operátoru souřadnice \(\hat{x}\). Nejdřív určíme střední hodnotu operátoru \(\hat{x}\) ve stavu \(\psi_1\). Počítáme integrál na symetrickém intervalu z liché funkce, neboť součinem tří lichých funkcí je opět funkce lichá

  \[\left\langle \hat{x}\right\rangle_{\psi_1}=\int_{-\frac{L}{2}}^{\frac{L}{2}}{\psi_1^\ast x\psi_1}\,\mathrm{d}x=\int_{-\frac{L}{2}}^{\frac{L}{2}}{x\psi_1^2}\,\mathrm{d}x=0,\]

  pak napíšeme střední hodnotu operátoru \(\hat{x}\) ve stavu \(\psi\)

  \[\left\langle \hat{x}\right\rangle_{\psi}=\left\langle \hat{x}\right\rangle_{\psi_1}+\frac{L}{2}=0+\frac{L}{2}=\frac{L}{2}.\]

   

  Analogicky spočítáme i střední hodnotu operátoru hybnosti \(\hat{p}\). Určíme střední hodnotu operátoru \(\hat{p}\) ve stavu \(\psi_1\). Počítáme integrál na symetrickém intervalu z liché funkce, neboť derivací liché funkce je funkce sudá a součinem sudé a liché funkce je opět funkce lichá

  \[\left\langle \hat{p}\right\rangle_{\psi_1}=\int_{-\frac{L}{2}}^{\frac{L}{2}}{\psi_1^\ast \left(-i\hbar\right)\frac{\mathrm{d}\psi_1}{\mathrm{d}x}}\,\mathrm{d}x=-i\hbar\int_{-\frac{L}{2}}^{\frac{L}{2}}{\psi_1 \frac{\mathrm{d}\psi_1}{\mathrm{d}x}}\,\mathrm{d}x=-i\hbar\cdot 0=0,\]

  střední hodnota operátoru \(\hat{p}\) ve stavu \(\psi\) je také nulová

  \[\left\langle \hat{p}\right\rangle_{\psi}=\left\langle \hat{p}\right\rangle_{\psi_1}=0.\]

   

  Při výpočtu středních hodnot druhých mocnin operátoru polohy a hybnosti máme vypočítat integrál ze sudé funkce na symetrickém intervalu, protože součinem dvou lichých funkcí je funkce sudá, součinem dvou sudých funkcí je opět funkce sudá a druhá derivace liché funkce je funkce lichá. Výpočet si tedy můžeme zjednodušit změnou integračních mezí.

  \[\left\langle \hat{x}^2\right\rangle_{\psi_1}=\int_{-\frac{L}{2}}^{\frac{L}{2}}{\psi_1^\ast x^2\psi_1}\,\mathrm{d}x=\int_{-\frac{L}{2}}^{\frac{L}{2}}{x^2\psi_1^2}\,\mathrm{d}x=2\int_{0}^{\frac{L}{2}}{x^2\psi_1^2}\,\mathrm{d}x\] \[\left\langle \hat{p}^2\right\rangle_{\psi_1}=\int_{-\frac{L}{2}}^{\frac{L}{2}}{\psi_1^\ast \left(-i\hbar\right)^2\frac{\mathrm{d}^2\psi_1}{\mathrm{d}x^2}}\,\mathrm{d}x=-\hbar^2\int_{-\frac{L}{2}}^{\frac{L}{2}}{\psi_1 \frac{\mathrm{d}^2\psi_1}{\mathrm{d}x^2}}\,\mathrm{d}x=-2\hbar^2\int_{0}^{\frac{L}{2}}{\psi_1 \frac{\mathrm{d}^2\psi_1}{\mathrm{d}x^2}}\,\mathrm{d}x\]

• Odpověď

  Normalizační konstanta vlnové funkce \(\psi\) je \(\left |A\right\vert=\sqrt{\frac{840}{L^7}}\).

  Střední hodnoty operátorů jsou \(\left\langle \hat{x}\right\rangle_\psi=\frac{L}{2}, \left\langle \hat{x}^2\right\rangle_\psi=\frac{L^2}{3}, \left\langle \hat{p}\right\rangle_\psi=0\) a \(\left\langle \hat{p}^2\right\rangle_\psi=\frac{42\hbar^2}{L^2}\).

  Ověřili jsme Heisenbergovu relaci neurčitosti, neboť \(\Delta x\Delta p=\sqrt{14}\frac{\hbar}{2}\).