Sbírka řešených úloh

SG experiment – superponovaný vs. smíšený stav

Úloha číslo: 4366

• Nápověda 1

  Připomeňte si nebo vyhledejte, jaký je rozdíl mezi superponovaným a smíšeným stavem.

• Řešení nápovědy 1

  Každá částice vstupující do měření v superponovaném stavu \(|\psi\rangle = \frac{\sqrt3}{2}|z+\rangle + \frac{1}{2}|z-\rangle\) se „současně“ nachází v obou stavech. Teprve při měření se rozhodne, zda naměříme kladný průmět a částice se bude po měření nacházet ve stavu \(|z+\rangle\), nebo naměříme záporný průmět a částice se bude po měření nacházet ve stavu \(|z-\rangle\). Pravděpodobnosti obou možností jsou \(75 ~ \%\), resp. \(25 ~ \%\).

  Ve smíšeném stavu bude v tomto případě průměrně \(75 ~ \%\) částic ve vlastním stavu \(|z+\rangle\) a \(25 ~ \%\) částic ve vlastním stavu \(|z-\rangle\). U konkrétně zvolené částice ovšem nemůžeme před měřením rozhodnout, ve kterém z těchto vlastních stavů se nachází.

• Nápověda 2

  Připomeňte si nebo vyhledejte, jak je třeba rozložit popis stavu vstupujícího do měření a jak lze z tohoto rozkladu určit pravděpodobnosti naměření jednotlivých hodnot.

• Řešení nápovědy 2

  Díky axiomu o měření víme, že stav, který vstupuje do měření, musíme rozložit na lineární kombinaci vlastních stavů měřené veličiny. Pravděpodobnosti naměření jednotlivých hodnot jsou rovny druhé mocnině velikosti příslušného koeficientu v této lineární kombinaci.

• Nápověda 3

  Spočítejte nebo vyhledejte tvar vlastních vektorů \(\hat S_z\) a \(\hat S_x\).

• Řešení nápovědy 3

  Operátory \(\hat S_z, \, \hat S_x\) průmětu spinu \(\frac{1}{2}\) mají jednotkové vlastní vektory \(|z+\rangle, \,\) \(|z-\rangle, \,\) \(|x+\rangle, \,\) a \(|x-\rangle\) příslušné vlastním číslům \(\lambda_{1, 2} = \pm \frac{\hbar}{2}\) ve tvaru

  \(+ \frac{\hbar}{2}\)	\(|z+\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}\)
  \(- \frac{\hbar}{2}\)	\(|z-\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}\)
  \(+ \frac{\hbar}{2}\)	\(|x+\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix}\)
  \(- \frac{\hbar}{2}\)	\(|x−\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} -1 \\ 1 \end{pmatrix}\)

• Aplet – popis a nastavení

  Na odkazu v zadání naleznete aplet zaměřený na rozdíl mezi superponovanými a smíšenými stavy. V tomto apletu v sekci Vysvětlení naleznete další nápovědy, které vám mohou pomoct s pochopením této problematiky.

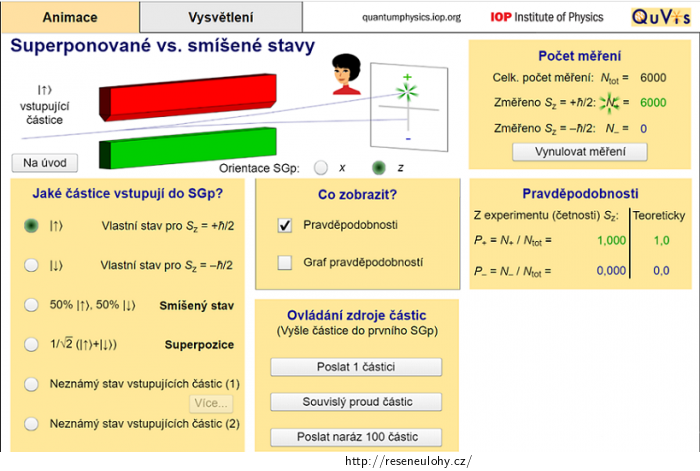
  Po otevření apletu klikněte na políčko Animace v levém horním rohu. Dole v levé části si můžete kliknutím zvolit, v jakém stavu budete posílat částice do Sternova–Gerlachova přístroje. Pod schématickým znázorněním tohoto přístroje v horní části máte možnost zvolit směr, do kterého bude Sternův–Gerlachův přístroj natočen. Pod tímto máte možnost zvolit zobrazení pravděpodobnosti a grafu pravděpodobnosti. Při práci s apletem důrazně doporučujeme nechat zaškrtnuté alespoň políčko Pravděpodobnosti. Uprostřed dolní části dále naleznete Ovládání zdroje částic. Zde si můžete zvolit, jak chcete částice do přístroje posílat. Měření doporučujeme provést opakovaným posíláním 100 částic naráz, jelikož by pro ostatní možnosti trvalo měření velmi dlouho. V pravé části se pak zobrazují výsledky měření. Pro inspiraci přikládáme záznam z apletu pro měření částic ve stavu \(|z+\rangle\), které vstupují do Sternova–Gerlachova přístroje natočeného ve směru osy \(z\). Nechali jsme zde zobrazit pouze Pravděpodobnosti. Všechna měření dále doporučujeme provádět pro dostatečně vysoký počet vstupujících částic (při hodnotách kolem 5000 částic se naměřené hodnoty velmi dobře shodují s teoretickými).

  

  Rovněž si zde můžete vyzkoušet úlohu opačnou než je tato. Po zaškrtnutí Neznámý stav vstupujících částic (1) a (2) provedete měření a určíte, zda se jedná o smíšený nebo superponovaný stav. Z naměřených hodnot pravděpodobností poté můžete určit vyjádření těchto stavů.

• Řešení – využití apletu

  Pošleme-li svazek částic v superponovaném stavu do Sternova–Gerlachova přístroje natočeného ve směru osy \(z\) zjistíme, že se pravděpodobnosti naměření obou průmětů spinu \(\frac{1}{2}\) shodují s pravděpodobnostmi, které bychom získali posláním svazku částic ve smíšeném stavu. V tomto měření se tedy superponovaný stav od smíšeného neliší.

  Nyní natočíme Sternův–Gerlachův přístroj do směru osy \(x\). Pošleme-li do přístroje svazek částic ve smíšeném stavu, naměříme oba průměty spinu s pravděpodobností \(\frac{1}{2}\). Pošleme-li do přístroje svazek částic v superponovaném stavu, naměříme každý průmět spinu s jinou pravděpodobností.

• Řešení – měření průmětu spinu 1/2 do směru osy z

  Uvažujme natočení Sternova–Gerlachova přístroje do směru osy \(z\). Superponovaný stav \(|\psi\rangle\) musíme dle axiomu o měření rozložit na lineární kombinaci vlastních stavů průmětu spinu \(\frac{1}{2}\) do směru osy \(z\), přičemž pravděpodobnosti naměření jednotlivých průmětů jsou rovny druhým mocninám koeficientů u příslušných vlastních stavů

  \[ |\psi\rangle = c_1|z+\rangle + c_2|z-\rangle \, , \]

  kde \(c_1, \, c_2\) jsou hledané komplexní konstanty. Jelikož však máme superponovaný stav ve tvaru \(|\psi\rangle = \frac{\sqrt3}{2}|z+\rangle + \frac{1}{2}|z-\rangle\), můžeme ihned říct, že

  \[ c_1 = \frac{\sqrt3}{2}, \, c_2 = \frac{1}{2}, \]

  a tedy

  \[ P_+ = |c_1|^2 = \left( \frac{\sqrt3}{2} \right)^2 = \frac{3}{4} = 75 \, \% \, , \] \[\] \[ P_- = |c_2|^2 = \left( \frac{1}{2} \right)^2 = \frac{1}{4} = 25 \, \% \, . \]

  Ve smíšeném stavu můžeme ihned říct, že pravděpodobnosti naměření kladného průmětu \(P_+\) a záporného průmětu \(P_-\) jsou

  \[ P_+ = \left( \frac{\sqrt3}{2} \right)^2 = \frac{3}{4} = 75 \, \% \, , \] \[\] \[ P_- = \left( \frac{1}{2} \right)^2 = \frac{1}{4} = 25 \, \% \, , \]

  jelikož jsou částice buď ve stavu \(|z+\rangle\) nebo ve stavu \(|z-\rangle\).

  Tímto jsme potvrdili výsledky získané z apletu pro měření do osy \(z\). Tj. při měření průmětu spinu \(\frac{1}{2}\) do směru osy \(z\) dávají oba případy stejné výsledky. Tímto měřením je tedy nelze odlišit.

• Řešení – měření průmětu spinu 1/2 do směru osy x

  Natočme nyní Sternův–Gerlachův přístroj do směru osy \(x\). Pro svazek částic ve smíšeném stavu bychom rozkládali stav \(|z+\rangle\) a \(|z-\rangle\) na lineární kombinaci stavů \(|x+\rangle\) a \(|x-\rangle\). Jelikož však platí (viz Návazné SG experimenty, Řešení)

  \[ |z+\rangle = \frac{1}{\sqrt{2}} |x+\rangle - \frac{1}{\sqrt{2}} |x-\rangle \]

  a analogicky

  \[ |z-\rangle = \frac{1}{\sqrt{2}} |x+\rangle + \frac{1}{\sqrt{2}} |x-\rangle \, , \]

  můžeme ihned říct, že v obou stavech je pravděpodobnost naměření obou průmětů do směru osy \(x\) stejná

  \[ P_+ = P_- = \left| \pm \frac{1}{\sqrt2} \right|^2 = \frac{1}{2} = 50 \, \% \, . \]

  Při natočení Sternova–Gerlachova přístroje do směru osy \(x\) tedy v případě svazku částic ve smíšeném stavu naměříme obě vlastní čísla \(+\frac{\hbar}{2}\) a \(-\frac{\hbar}{2}\) s pravděpodobností \(50 \%\) pro každou individuální částici.

  Pro svazek částic v superponovaném stavu provedeme rozklad na lineární kombinaci vlastních stavů průmětu spinu \(\frac{1}{2}\) do směru osy \(x\)

  \[ |\psi\rangle = d_1|x+\rangle + d_2|x-\rangle \, , \]

  kde \(d_1, \, d_2\) jsou hledané komplexní konstanty. Dosadíme

  \[ |\psi\rangle = \frac{\sqrt3}{2}|z+\rangle + \frac{1}{2}|z-\rangle = \frac{\sqrt3}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \frac{1}{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \, , \] \[ |x+\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \, , \] \[ |x-\rangle = \frac{1}{\sqrt{2}} \begin{pmatrix} -1 \\ 1 \end{pmatrix} \, . \]

  Protože tentokrát není rozklad vidět „bez počítání“ jako v předchozí části, hledané koeficienty \(d_1, \, d_2\) určíme pomocí skalárního součinu jako

  \[ d_1 = \left \langle x+ | \, \psi \right \rangle \, , \] \[ d_2 = \left \langle x- | \, \psi \right \rangle \, . \]

  Výpočet provedeme pro koeficient \(d_1\)

  \[ d_1 = \langle x+ | \, \psi\rangle = \frac{1}{\sqrt2} \begin{pmatrix} 1 & 1 \end{pmatrix} \left[ \frac{\sqrt3}{2} \begin{pmatrix} 1 \\ 0 \end{pmatrix} + \frac{1}{2} \begin{pmatrix} 0 \\ 1 \end{pmatrix} \right] = \] \[ = \frac{\sqrt3}{2\sqrt2} + \frac{1}{2\sqrt2} = \frac{1+\sqrt3}{2\sqrt2} \, . \]

  Výpočet koeficientu \(d_2\) je zcela analogický, proto zde uvedeme pouze výsledek

  \[ d_2 = \frac{1-\sqrt3}{2\sqrt2} \, . \]

  Nyní určíme pravděpodobnost naměření obou průmětů spinu \(\frac{1}{2}\) do daného směru. Pravděpodobnosti naměření jednotlivých hodnot jsou rovny druhé mocnině velikosti příslušného koeficientu, tj.

  \[ P_+ = |d_1|^2 \doteq 93{,}3 \, \% \, , \] \[ P_- = |d_2|^2 \doteq 6{,}7 \, \% \, . \]

  Tímto jsme potvrdili závěry, ke kterým jsme dospěli při práci s apletem, tj. tímto měřením můžeme dané stavy odlišit.

  Pozn.: Povšimněte si podobnosti stavu \(|\psi\rangle\) s vlastním stavem popsaným vlastním vektorem \(\vec v\) v úloze Průmět spinu 1/2 do směru v rovině xz, Řešení c).

• Odpověď

  Pravděpodobnosti naměření obou průmětů spinu \(\frac{1}{2}\) do směru osy \(z\) jsou totožné pro oba svazky vstupující do měření. Jejich hodnoty jsou

  \[ P_+ = \frac{3}{4} = 75 ~ \% \, , \] \[\] \[ P_- = \frac{1}{4} = 25 ~ \% \, . \]

  Pravděpodobnosti naměření obou průmětů spinu \(\frac{1}{2}\) do směru osy \(x\) jsou pro smíšený stav

  \[ P_+ = P_- = \frac{1}{2} = 50 ~ \% \]

  a pro superponovaný stav

  \[ P_+ = \left| \frac{1+\sqrt3}{2\sqrt2} \right|^2 \doteq 93{,}3 ~ \% \, , \] \[ P_- = \left| \frac{1-\sqrt3}{2\sqrt2} \right|^2 \doteq 6{,}7 ~ \% \, . \]

  Pomocí měření průmětu spinu \(\frac{1}{2}\) do směru osy \(x\) lze tedy oba případy rozlišit.