Sbírka řešených úloh

Pravděpodobnost nalezení elektronu za Bohrovým poloměrem

Úloha číslo: 2018

• Nápověda 1

  Uvědomte si, co určuje Bohrův poloměr. Vyhledejte si jeho velikost.

• Řešení nápovědy 1

  Bohrův model atomu je planetární model, předpokládá pohyb elektronů po určitých kruhových drahách, na kterých se elektrony pohybují bez vyzařování energie. Bohrův poloměr je poloměr kruhové dráhy elektronu v základním stavu atomu vodíku. Velikost Bohrova poloměru \(a_B\) odpovídá skutečnému poloměru atomu vodíku

  \(a_B=\frac{4\pi\varepsilon_0\hbar^2}{m_ee^2}\approx 0{,}052 917 7{\cdot} 10^{-9}\)m,

  kde \(\varepsilon_0\) je permitivita vakua, \(\hbar\) je redukovaná Planckova konstanta, \(m_e\) je hmotnost elektronu a \(e\) je velikost elementárního náboje.

• Nápověda 2

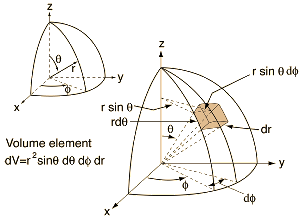
  Zamyslete se, jak se vypočítá pravděpodobnost nalezení elektronu v dané oblasti prostoru.

• Řešení nápovědy 2

  Protože problém, který řešíme, je sféricky symetrický, bude výhodné počítat ve sférických souřadnicích \(r\), \(\vartheta\) a \(\varphi\). Souřadnice \(r\in\langle0, \infty)\) udává vzdálenost od počátku soustavy souřadnic, souřadnice \(\vartheta\in\langle 0, \pi\rangle\) a \(\varphi\in\langle 0, 2\pi )\) určují postupně úhel odklonu od osy \(z\) a od osy \(x\) v kartézské soustavě souřadnic.

  Zajímá nás jen určitá oblast prostoru, proto si vyjádříme ve sférických souřadnicích objem \(\mathrm{d}V\) velmi malé části prostoru vymezené souřadnicemi \((r, r+\mathrm{d}r), (\vartheta, \vartheta+\mathrm{d}\vartheta)\) a \((\varphi, \varphi+\mathrm{d}\varphi)\) \[\mathrm{d}V=r^2\,\mathrm{d}r\sin{\vartheta}\,\mathrm{d}\vartheta\,\mathrm{d}\varphi.\]

   

  

  Poznámka: Obrázek byl převzat ze stránky hyperphysics.

  Vlnová funkce \(\psi_{nlm}(r, \vartheta, \varphi)\) popisující ve sférických souřadnicích stav elektronu se skládá z radiální části \(R_{nl}(r)\) a z úhlové části \(Y_{lm}(\vartheta, \varphi)\) \[\psi_{nlm}(r, \vartheta, \varphi)=R_{nl}(r)Y_{lm}(\vartheta, \varphi),\] kde \(n, l, m\) jsou kvantová čísla. Radiální část \(R_{nl}(r)\) udává změny vlnové funkce v závislosti na poloměru \(r\) a úhlová část \(Y_{lm}(\vartheta, \varphi)\) popisuje změny vlnové funkce v závislosti na změnách úhlů \(\vartheta\) a \(\varphi\).

   

  Pravděpodobnost \(\mathrm{d}p(r,\vartheta, \varphi)\) nalézt elektron v části prostoru o objemu \(\mathrm{d}V\) je úměrná druhé mocnině velikosti vlnové funkce \(\psi_{nlm}\) \[\mathrm{d}p(r,\vartheta, \varphi)=|\psi_{nlm}(r, \vartheta, \varphi)|^2\,\mathrm{d}V=|R_{nl}(r)Y_{lm}(\vartheta, \varphi)|^2r^2\,\mathrm{d}r\sin{\vartheta}\,\mathrm{d}\vartheta\,\mathrm{d}\varphi.\]

  My však hledáme pravděpodobnost nalezení elektronu v závislosti pouze na vzdálenosti \(r\) od jádra, tedy velikosti úhlů \(\vartheta\) a \(\varphi\) mohou být libovolné, proto zintegrujeme \(\mathrm{d}p(r,\vartheta, \varphi)\) přes úhly \(\vartheta\in\langle 0, \pi\rangle\) a \(\varphi\in\langle 0, 2\pi )\). Úhlová část vlnové funkce \(Y_{lm}(\vartheta, \varphi)\) je normována tak, aby integrace druhé mocniny její velikosti přes plný prostorový úhel byla rovna jedné. Tudíž se pravděpodobnost \(\mathrm{d}p(r)\) nalezení elektronu v části prostoru vymezené pouze poloměrem \((r, r+\mathrm{d}r)\) vypočítá \[\mathrm{d}p(r)=|R_{nl}(r)|^2r^2\,\mathrm{d}r.\]

  Pravděpodobnost \(P_{nl}\), že elektron nalezneme ve větší vzdálenosti od jádra, než odpovídá Bohrovu poloměru \(a_B\), je dána vztahem \[P_{nl}=\int_{a_B}^\infty\,\mathrm{d}p(r)=\int_{a_B}^\infty{|R_{nl}(r)|^2r^2}\,\mathrm{d}r,\] kde \(R_{nl}(r)\) je radiální část vlnové funkce, \(n\) a \(l\) jsou kvantová čísla.

• Nápověda 3

  Zjistěte, jaký tvar má radiální část vlnové funkce popisující elektron v základním stavu atomu vodíku.

• Řešení nápovědy 3

  Základní stav atomu vodíku je určen kvantovými čísly \(n=1\), \(l=0\), \(m=0\) a protonovým číslem \(Z=1\).

  Radiální část vlnové funkce atomu vodíku v základním stavu popisuje funkce

  \[R_{10}(r)=\left(\frac{Z}{a_B}\right)^{\frac{3}{2}}2\,\mathrm{e}^{-\frac{Zr}{a_B}}=\frac{2}{a_B^{3/2}}\,\mathrm{e}^{-\frac{r}{a_B}}.\]

• Řešení

  Poloměr klasické dráhy, tzv. Bohrův poloměr \(a_B,\) udává poloměr kruhové dráhy, po které se pohybuje elektron v základním stavu v atomu vodíku, aniž by přitom vyzařoval energii.

  \(a_B=\frac{4\pi\varepsilon_0\hbar^2}{m_ee^2}\approx 0{,}052 917 7{\cdot} 10^{-9}\)m

  Atom vodíku je sféricky symetrický, proto bude výhodné úlohu řešit ve sférických souřadnicích \(r, \vartheta\) a \(\varphi\).

  Pravděpodobnost \(P_{nl}\) nalezení elektronu v základním stavu atomu vodíku v závislosti na vzdálenosti \(r\) od jádra, konkrétně je-li vzdálenost \(r\) větší než Bohrův poloměr \(a_B\), je dána vztahem \[P_{nl}=\int_{a_B}^\infty{|R_{nl}(r)|^2r^2}\,\mathrm{d}r,\] kde \(n\) a \(l\) jsou kvantová čísla základního stavu atomu vodíku a \(R_{nl}(r)\) je radiální část vlnové funkce atomu vodíku v základním stavu. Odvození je uvedeno v Řešení nápovědy 2.

   

  Základní stav atomu vodíku je určen kvantovými čísly \(n=1\), \(l=0\), \(m=0\) a protonovým číslem \(Z=1\). Radiální část \(R_{10}(r)\) vlnové funkce atomu vodíku v základním stavu popisuje funkce

  \[R_{10}(r)=\left(\frac{Z}{a_B}\right)^{\frac{3}{2}}2\,\mathrm{e}^{-\frac{Zr}{a_B}}=\frac{2}{a_B^{3/2}}\,\mathrm{e}^{-\frac{r}{a_B}}.\]

  Nyní můžeme dosadit do \(P_{nl}\) a vypočítat pravděpodobnost \(P_{10}\), že elektron v základním stavu atomu vodíku nalezneme ve větší vzdálenosti od jádra, než odpovídá Bohrovu poloměru \(a_B\).

  \[P_{10}=\int_{a_B}^\infty{|R_{10}(r)|^2r^2}\,\mathrm{d}r=\int_{a_B}^\infty{\left[\frac{2}{a_B^{3/2}}\,\mathrm{e}^{-\frac{r}{a_B}}\right]^2r^2}\,\mathrm{d}r=\]

  Funkci umocníme, konstanty vytkneme před integrál, dosadíme hodnotu integrálu (viz Výpočet integrálu) a upravíme.

  \[=\int_{a_B}^\infty{\frac{4}{a_B^3}\,\mathrm{e}^{-\frac{2r}{a_B}}r^2}\,\mathrm{d}r=\frac{4}{a_B^3}\int_{a_B}^\infty{r^2\,\mathrm{e}^{-\frac{2r}{a_B}}}\,\mathrm{d}r=\frac{4}{a_B^3}\frac{5a_B^3}{4\,\mathrm{e}^2}=\frac{5}{\mathrm{e}^2}\doteq 0{,}68=68\,\text{%} \]

  Pravděpodobnost, že elektron v základním stavu atomu vodíku nalezneme ve větší vzdálenosti od jádra, než odpovídá Bohrovu poloměru, je 68 %.

• Výpočet integrálu

  Při výpočtu integrálu použijeme dvakrát integraci per partes \[\int (u v^{\prime})\,\mathrm{d}r=uv-\int(u^{\prime} v)\,\mathrm{d}r\] a následující základní derivace a integrály \[(ar^n)^{\prime}=anr^{n-1},\] \[\int{\mathrm{e}^{br}}\,\mathrm{d}r=\frac{1}{b}\mathrm{e}^{br}+C,\] kde \(a,\, b,\, n\) jsou konstanty \((b\neq 0)\) a \(C\) je integrační konstanta.

   

  Nejdříve vypočteme neurčitý integrál, pak určíme hodnotu určitého integrálu.

  Při prvním použití metody per partes zvolíme \(u=r^2\) a \(v^{\prime}=\mathrm{e}^{-\frac{2r}{a_B}}\), spočítáme \(u^{\prime}=2r\) a \(v=-\frac{a_B}{2}\mathrm{e}^{-\frac{2r}{a_B}}\), dosadíme a upravíme.

  \[\int{r^2\,\mathrm{e}^{-\frac{2r}{a_B}}}\,\mathrm{d}r=r^2\left(-\frac{a_B}{2}\mathrm{e}^{-\frac{2r}{a_B}}\right)-\int{2r\left(-\frac{a_B}{2}\,\mathrm{e}^{-\frac{2r}{a_B}}\right)}\,\mathrm{d}r=-\frac{a_B}{2}r^2\,\mathrm{e}^{-\frac{2r}{a_B}}+\int{a_Br\,\mathrm{e}^{-\frac{2r}{a_B}}}\,\mathrm{d}r=\]

  Při druhém použití metody per partes zvolíme \(u=a_Br\) a \(v^{\prime}=\mathrm{e}^{-\frac{2r}{a_B}}\), spočítáme \(u^{\prime}=a_B\) a \(v=-\frac{a_B}{2}\mathrm{e}^{-\frac{2r}{a_B}}\), dosadíme a upravíme.

  \[=-\frac{a_B}{2}r^2\,\mathrm{e}^{-\frac{2r}{a_B}}+a_Br\left(-\frac{a_B}{2}\mathrm{e}^{-\frac{2r}{a_B}}\right)-\int{a_B\left(-\frac{a_B}{2}\,\mathrm{e}^{-\frac{2r}{a_B}}\right)}\,\mathrm{d}r=-\frac{a_B}{2}r^2\,\mathrm{e}^{-\frac{2r}{a_B}}-\frac{a_B^2}{2}r\,\mathrm{e}^{-\frac{2r}{a_B}}+\int{\frac{a_B^2}{2}\,\mathrm{e}^{-\frac{2r}{a_B}}}\,\mathrm{d}r=\]

  Spočítáme poslední integrál, upravíme a máme vyjádřen neurčitý integrál.

  \[=-\frac{a_B}{2}r^2\,\mathrm{e}^{-\frac{2r}{a_B}}-\frac{a_B^2}{2}r\,\mathrm{e}^{-\frac{2r}{a_B}}-\frac{a_B^3}{4}\,\mathrm{e}^{-\frac{2r}{a_B}}+C=-\frac{a_B}{4}\,\mathrm{e}^{-\frac{2r}{a_B}}\left(2r^2+2a_Br+a_B^2\right)+C\]

  Nyní vypočítáme určitý integrál dosazením integračních mezí.

  \[\int_{a_B}^\infty{r^2\,\mathrm{e}^{-\frac{2r}{a_B}}}\,\mathrm{d}r=\left[-\frac{a_B}{4}\,\mathrm{e}^{-\frac{2r}{a_B}}\left(2r^2+2a_Br+a_B^2\right)+C\right]_{a_B}^\infty=\frac{5a_B^3}{4\,\mathrm{e}^2}\]

   

  Na závěr uvedeme postup, jak vypočítat integrál v rozhraní WolframAlpha.

  Do řádku pro výpočet zadáme integrál \(\int_{a_B}^\infty{r^2\,\mathrm{e}^{-\frac{2r}{a_B}}}\,\mathrm{d}r\) ve tvaru

  integrate r^2 * e^(-2*r/a) dr from r=a to infty,

  stiskneme tlačítko = (compute) a zjistíme výsledek

  \[\int_{a_B}^\infty{r^2\,\mathrm{e}^{-\frac{2r}{a_B}}}\,\mathrm{d}r=\frac{5a_B^3}{4\,\mathrm{e}^2}.\]

• Odpověď

  Pravděpodobnost, že elektron v základním stavu atomu vodíku nalezneme ve větší vzdálenosti od jádra, než odpovídá Bohrovu poloměru, je 68 %.