Sbírka řešených úloh

Vlastnosti stavu s ostrými hodnotami L² a L_z

Úloha číslo: 4361

• Nápověda 1

  Připomeňte si nebo vyhledejte, jak určujeme průmět momentu hybnosti do směru \(\vec n\). Využijte vyjádření vektoru \(\vec n\) ve sférických souřadnicích.

• Řešení nápovědy 1

  Jednotkový vektor ve směru \(\vec n\) má ve sférických souřadnicích tvar

  \[ \vec n = \left (\sin \vartheta \cos \varphi, \, \sin \vartheta \sin \varphi, \, \cos \vartheta \right ) \, . \]

  K určení průmětu momentu hybnosti do tohoto směru využijeme skalární součin

  \[ \hat L_{\vec n} = \hat L \cdot \vec n = \hat L_x \sin \vartheta \cos \varphi + \hat L_y \sin \vartheta \sin \varphi + \hat L_z \cos \vartheta \, . \]

• Nápověda 2

  Připomeňte si, jak lze určit střední hodnotu veličiny \(F\) ve stavu popsaném normovanou vlnovou funkcí \(\psi\). Dále si připomeňte nebo vyhledejte definici lineárního hermitovského operátoru.

• Řešení nápovědy 2

  Střední hodnotu veličiny \(F\) ve stavu popsaném normovanou vlnovou funkcí \(\psi\) lze určit dle vztahu \[\langle F \rangle_{\psi} = \left \langle \psi \, \Big | \, \hat F \psi \right \rangle = \psi^{\dagger} \hat F \psi \, ,\] kde \(\hat F\) je operátor příslušející veličině \(F\) a křížek značí hermitovsky sdruženou matici, tj. matici transponovanou a komplexně sdruženou.

  Lineární operátor \(\hat G\) je hermitovský, pokud pro libovolné dvě vlnové funkce \(\varphi\) a \(\psi\) z Hilbertova prostoru platí

  \[ \left \langle \varphi \, \Big | \, \hat G \psi \right \rangle = \left \langle \hat G \varphi \, \Big | \, \psi \right \rangle \, . \]

• Nápověda 3

  Připomeňte si nebo vyhledejte, co pro danou částici znamená, že se nachází ve stavu \(\psi = |lm\rangle\) s ostrými hodnotami \(L^2\) a \(L_z\).

• Řešení nápovědy 3

  Stav \(\psi = |lm\rangle\) s ostrými hodnotami \(L^2\) a \(L_z\) znamená, že měření těchto veličin má nulovou odchylku a střední hodnoty těchto veličin jsou rovny příslušným vlastním číslům, tj. v tomto stavu platí

  \[ \left \langle L^2 \right \rangle_\psi = \hbar^2 l \left (l+1 \right ) \, , \] \[ \left \langle L_z \right \rangle_\psi = m\hbar \, . \]

  Při výpočtu středních hodnot ostatních složek momentu hybnosti či jejich kvadrátů bude tedy vhodné vyjádřit daný operátor pomocí operátorů \(\hat L_z\) a \(\hat L^2\), jejichž střední hodnoty známe. K tomu lze využít jak vztah mezi složkami a velikostí vektorového operátoru, tak relace neurčitosti mezi složkami operátoru momentu hybnosti.

• Řešení a)

  Operátor průmětu momentu hybnosti do směru \(\vec n\) má tvar (viz Nápověda 1)

  \[ \hat L_{\vec n} = \hat L_x \sin \vartheta \cos \varphi + \hat L_y \sin \vartheta \sin \varphi + \hat L_z \cos \vartheta \, . \]

  K určení jeho střední hodnoty potřebujeme určit střední hodnoty operátorů \(\hat L_x, \, \hat L_y, \, \hat L_z\). Zaměřme se nyní na \(x\)-ovou a \(y\)-ovou složku. Z komutačních relací složek momentu hybnosti (viz Komutátory se složkou momentu hybnosti, Odpověď) víme, že

  \[ \hat L_x = \frac{1}{i\hbar}\left( \hat L_y \hat L_z - \hat L_z \hat L_y \right) \, , \] \[ \hat L_y = \frac{1}{i\hbar}\left( \hat L_z \hat L_x - \hat L_x \hat L_z \right) \, . \]

  Střední hodnotu \(L_x\) ve stavu \(\psi = |lm\rangle\) tedy určíme jako

  \[ \left \langle L_x \right \rangle_\psi = \left \langle \frac{1}{i\hbar} \left( \hat L_y \hat L_z - \hat L_z \hat L_y \right) \right \rangle_\psi = \frac{1}{i\hbar} \left ( \left \langle \hat L_y \hat L_z \right \rangle_\psi - \left \langle \hat L_z \hat L_y \right \rangle_\psi \right ) \, . \]

  Při výpočtu středních hodnot v závorce výše vyjdeme z obecného vztahu pro střední hodnotu, do kterého dosadíme

  \[ \left \langle \hat L_z \hat L_y \right \rangle_\psi = \left \langle \psi \, \Big | \, \hat L_z \hat L_y \psi \right \rangle \, . \]

  Nyní využijeme toho, že složky momentu hybnosti jsou lineární hermitovské operátory, díky čemuž můžeme provést úpravu (viz Nápověda 2)

  \[ \left \langle \psi \, \Big | \, \hat L_z \hat L_y \psi \right \rangle = \left \langle \hat L_z \psi \, \Big | \, \hat L_y \psi \right \rangle \, . \]

  Jelikož má částice ve stavu \(\psi = |lm\rangle\) ostré hodnoty \(L_z\), můžeme dosadit \(\hat L_z \psi = m\hbar \, \psi\), čímž dostaneme

  \[ \left \langle \hat L_z \hat L_y \right \rangle_\psi = \left \langle m\hbar \, \psi \, \Big | \, \hat L_y \psi \right \rangle = m\hbar \left \langle \psi \, \Big | \, \hat L_y \psi \right \rangle = m\hbar \, \left \langle L_y \right \rangle_\psi \, . \]

  Analogicky dostaneme

  \[ \left \langle \hat L_y \hat L_z \right \rangle_\psi = m\hbar \, \left \langle L_y \right \rangle_\psi \, . \]

  Dosazením těchto středních hodnot a úpravou získáme výsledek

  \[ \left \langle L_x \right \rangle_\psi = \frac{1}{i\hbar} \left ( \left \langle \hat L_y \hat L_z \right \rangle_\psi - \left \langle \hat L_z \hat L_y \right \rangle_\psi \right ) = \frac{1}{i\hbar} \left ( m\hbar \, \left \langle L_y \right \rangle_\psi - m\hbar \, \left \langle L_y \right \rangle_\psi \right ) = 0 \, . \]

  Výpočet pro \(\left \langle L_y \right \rangle_\psi\) je zcela anlogický, proto zde uvádíme pouze výsledek

  \[ \left \langle L_y \right \rangle_\psi = 0 \, . \]

  Výraz pro střední hodnotu průmětu momentu hybnosti do směru \(\vec n\) ve stavu \(\psi = |lm\rangle\) se po dosazení výsledků určených výše zredukuje na tvar

  \[ \langle L_{\vec n} \rangle_\psi = 0 \cdot \sin \vartheta \cos \varphi + 0 \cdot \sin \vartheta \sin \varphi + \langle L_z \rangle_\psi \cos \vartheta = \langle L_z \rangle_\psi \cos \vartheta \, . \]

  Nyní opět můžeme dosadit \(\langle L_z\rangle_\psi = m\hbar\), čímž získáme výsledek

  \[ \langle L_{\vec n} \rangle_\psi = m\hbar \cos \vartheta \, . \]

• Řešení b)

  Jelikož \(\hat L^2 = \hat L_x^2 + \hat L_y^2 + \hat L_z^2 \,\), platí \(\left \langle L^2 \right \rangle = \left \langle L_x^2 \right \rangle + \left \langle L_y^2 \right \rangle + \left \langle L_z^2 \right \rangle\). Ze symetrie usuzujeme, že pro částici ve stavu \(\psi = |lm\rangle\) platí \(\left \langle L_x^2 \right \rangle_\psi = \left \langle L_y^2 \right \rangle_\psi\). Odtud můžeme říct, že

  \[ \left \langle L_x^2 \right \rangle_\psi = \left \langle L_y^2 \right \rangle_\psi = \frac{1}{2} \left ( \left \langle L^2 \right \rangle_\psi - \left \langle L_z^2 \right \rangle_\psi \right ) \, . \]

  Jelikož má částice ve stavu \(\psi = |lm\rangle\) ostré hodnoty \(L_z\) a \(L^2\), můžeme dosadit

  \[ \langle L_z\rangle_\psi = m\hbar \, , \] \[ \langle L^2\rangle_\psi = \hbar^2 \, l(l+1) \, , \]

  čímž dostaneme

  \[ \left \langle L_x^2 \right \rangle_\psi = \left \langle L_y^2 \right \rangle_\psi = \frac{1}{2} \left [ \hbar^2 \, l(l+1) - m^2\hbar^2 \right ] = \frac{\hbar^2}{2} \left [ l(l+1) - m^2 \right ] \, . \]

  Povšimněte si, že ve stavu \(\psi = |lm\rangle\) platí \(\left \langle L_x \right \rangle_\psi = \left \langle L_y \right \rangle_\psi = 0 \,\) a zároveň \(\left \langle L_x^2 \right \rangle_\psi = \left \langle L_y^2 \right \rangle_\psi \neq 0 \,\). Nemůžeme tedy říct, že by moment hybnosti mířil podél osy \(z\). Tomuto postřehu se detailněji věnujeme v sekci Komentář.

• Odpověď

  a) Ve stavu \(\psi = |lm\rangle\) s ostrými hodnotami \(L^2\) a \(L_z\) je střední hodnota průmětu momentu hybnosti do směru \(\vec n\)

  \[ \langle L_{\vec n} \rangle_\psi = m\hbar \cos \vartheta \, . \]

  b) Ve stavu \(\psi = |lm\rangle\) s ostrými hodnotami \(L^2\) a \(L_z\) platí

  \[ \left \langle L_x^2 \right \rangle_\psi = \left \langle L_y^2 \right \rangle_\psi = \frac{\hbar^2}{2} \left [ l(l+1) - m^2 \right ] \, . \]

• Komentář – klasický model

  Z výpočtů výše víme, že ve stavu \(\psi = |lm\rangle\) platí \(\left \langle L_x \right \rangle_\psi = \left \langle L_y \right \rangle_\psi = 0 \,\) a zároveň střední hodnoty \(\left \langle L_x^2 \right \rangle_\psi = \left \langle L_y^2 \right \rangle_\psi\) jsou nenulové. Složky momentu hybnosti \(L_x\) a \(L_y\) se tedy „vystředují“ na nulu, ale nemůžeme říct, že by moment hybnosti mířil podél osy \(z\). Jako klasický model kvantověmechanického stacionárního stavu \(\psi = |lm\rangle\) se používá soubor momentů hybnosti, které jsou náhodně rozloženy na povrchu pláště kužele s vrcholovým úhlem \(\vartheta_m\) (viz obrázek níže). K charakterizaci tohoto modelu potřebujeme určit onen vrcholový úhel.

  

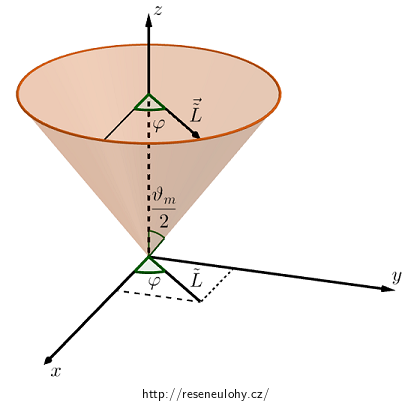
  Nejprve ověříme, že v tomto modelu složky \(L_x\) a \(L_y\) mají nulovou střední hodnotu. Průměty do os \(x\) a \(y\) mají dle zvoleného značení tvar

  \[ L_x = \tilde{L} \cos \varphi \, , \] \[ L_y = \tilde{L} \sin \varphi \, , \]

  kde \(\varphi \in \langle 0, \, 2\pi \rangle\).

  Střední hodnotu určíme pro \(L_x\)

  \[ \langle L_x\rangle = \int_0^{2\pi} \tilde{L} \cos \varphi \, \mathrm{d}\varphi \, . \]

  Zde integrujeme funkci kosinus přes její periodu. Hodnota určitého integrálu výše je tedy nulová, tj.

  \[ \langle L_x\rangle = 0 \, . \]

  Analogicky bychom spočítali

  \[ \langle L_y\rangle = 0 \, . \]

  Nyní určíme střední hodnoty \(\left \langle L_x^2 \right \rangle\) a \(\left \langle L_y^2 \right \rangle\). Výpočet provedeme pro \(\left \langle L_x^2 \right \rangle\)

  \[ \left \langle L_x^2 \right \rangle = \int_0^{2\pi} \tilde{L}^2 \cos^2 \varphi \, \mathrm{d}\varphi = \tilde{L}^2 \int_0^{2\pi} \frac{1 + \cos 2\varphi}{2} \, \mathrm{d}\varphi = \tilde{L}^2 \int_0^{2\pi} \frac{1}{2} + \frac{\cos 2\varphi}{2} \, \mathrm{d}\varphi \, . \]

  Tentokrát integrujeme funkci kosinus přes dvě periody. Tato část určitého integrálu je tedy opět nulová. Celkově pak dostaneme

  \[ \left \langle L_x^2 \right \rangle = \pi \tilde{L}^2 \, . \]

  Analogicky bychom spočítali

  \[ \left \langle L_y^2 \right \rangle = \pi \tilde{L}^2 \, . \]

  Tímto jsme ověřili, že model kužele splňuje \(\left \langle L_x \right \rangle = \left \langle L_y \right \rangle = 0 \,\) a zároveň střední hodnoty \(\left \langle L_x^2 \right \rangle = \left \langle L_y^2 \right \rangle\) jsou nenulové.

  K určení vrcholového úhlu kužele využijeme výsledky určené v oddílu Řešení b). Zaměříme-li se pouze na polovinu vrcholového úhlu \(\vartheta_m\), můžeme využít funkci kosinus a tento úhel určit jako

  \[ \cos \frac{\vartheta_m}{2} = \frac{\langle L_z \rangle}{\sqrt{\langle L^2 \rangle}} = \frac{\langle L_z \rangle} {\sqrt{\langle L_x \rangle^2 + \langle L_y \rangle^2 + \langle L_z \rangle^2}} = \] \[ = \frac{m\hbar}{\sqrt{m^2\hbar^2 + \hbar^2 \left [ l \left (l+1 \right ) - m^2 \right ]}} = \frac{m}{\sqrt{m^2 + l \left (l+1 \right ) - m^2 }} = \frac{m}{\sqrt{l \left (l+1 \right )}} \, . \]

  Celkově tedy můžeme říct, že klasickým modelem kvantověmechanického stacionárního stavu \(|lm\rangle\) je soubor momentů hybnosti, které jsou náhodně rozloženy na povrchu pláště kužele s vrcholovým úhlem \(\vartheta_m\), pro který platí

  \[ \cos \frac{\vartheta_m}{2} = \frac{m}{\sqrt{l \left (l+1 \right )}} \, . \]