Sbírka řešených úloh

Tlak na stěnu sférické jámy

Úloha číslo: 712

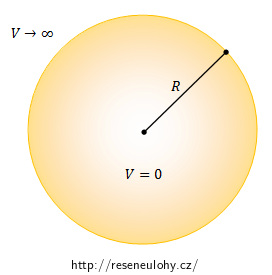
Částice o hmotnosti m je vázána uvnitř sféry o poloměru R s neprostupnými stěnami: potenciál V(r) = 0 pro r ≤ R a V(r) → ∞ pro r > R. Částice se nachází v základním, sféricky symetrickém stavu, který je popsán vlnovou funkcí

\[\psi_1(r)=\sqrt{\frac{2}{R}}\,\sin\left(\frac{\pi r}{R}\right)\,,\]

a přísluší jí energie \(E_1=\frac{\pi^2 \hbar^2}{2m R^2}\). Určete tlak na vnitřní stěnu sféry

a) nejprve obecně,

b) pro elektron a sféru o poloměru R = 10⁻¹⁰ m (tj. řádově rozměr atomu),

c) pro proton v jádře atomu o poloměru R = 10⁻¹⁵ m.

• Nápověda – tlak

  Na čem závisí tlak na vnitřní stěnu sféry o poloměru R?

• Řešení nápovědy – tlak

  Tlak je obecně roven síle působící kolmo na jednotku plochy. Pro případ sféry o poloměru R tedy

  \[p=\frac{F}{4\pi R^2}\,.\]

• Nápověda – síla

  Jak souvisí síla, kterou částice působí na stěnu jámy, s její energií?

• Řešení nápovědy – síla

  Pokud se v systému neztrácí energie jinak než deformací (změnou poloměru) jámy, platí, že zapůsobí-li částice zevnitř silou na stěnu jámy a posune ji tím o δR (rozšíří), vykoná práci F·δR rovnou úbytku její energie, tedy F·δR = E₁(R) − E₁(R+δR). Odtud

  \[F=-\frac{E_1(R+\delta R)-E_1(R)}{\delta R}\,,\]

  resp. v limitním případě (neboť jáma se ve skutečnosti nezvětšuje)

  \[F=-\frac{\partial E_1}{\partial R}\,.\]

  Síla, kterou částice tlačí na stěnu jámy, souvisí s tím, jak by se měnila její energie při měnícím se poloměru jámy.

• Řešení

  a) Částici v základním stavu přísluší energie

  \[E_1=\frac{\pi^2 \hbar^2}{2m R^2}.\]

  Síla, kterou částice působí na vnitřní stěnu sféry, je rovna minus derivaci energie (viz nápověda), a proto bude mít velikost

  \[F=-\frac{\partial E_1}{\partial R}=\frac{\pi^2 \hbar^2}{m R^3}\,.\]

  Tlak na vnitřní stěnu sféry o poloměru R bude

  \[p=\frac{F}{4\pi R^2}=\frac{\pi \hbar^2}{4m R^5}\,.\]

  b) Pro případ elektronu a sféru o poloměru R = 10⁻¹⁰ m bude

  \[p=\frac{\pi \hbar^2}{4m_e R^5}\,,\]

  kde hmotnost elektronu m_e = 9,11·10⁻³¹ kg. Vychází

  \[p=\frac{\pi\,\cdot\,\left(1{,}055{\cdot}10^{-34}\right)^2}{4\,\cdot\,9{,}11{\cdot}10^{-31}\,\cdot\,\left(10^{-10}\right)^5}\ \mbox{Pa}\,=\frac{\pi\,\cdot\,1{,}055^2}{4\,\cdot\,9{,}11}\,\cdot\,10^{13}\ \mbox{Pa}\,\dot{=}\, 1{,}0 \cdot\,10^{12}\,\mbox{Pa}\,.\]

  c) Pro případ protonu v jádře atomu bude

  \[p=\frac{\pi \hbar^2}{4m_p R^5}\,,\]

  kde hmotnost protonu m_p = 1,673·10⁻²⁷ kg a poloměr R = 10⁻¹⁵ m. Vychází

  \[p=\frac{\pi\,\cdot\,\left(1{,}055{\cdot}10^{-34}\right)^2}{4\,\cdot\,1{,}673{\cdot}10^{-27}\,\cdot\,\left(10^{-15}\right)^5}\ \mbox{Pa}\,=\frac{\pi\,\cdot\,1{,}055^2}{4\,\cdot\,1{,}673}\,\cdot\,10^{34}\ \mbox{Pa}\,\dot{=}\, 5{,}2 \cdot\, 10^{33}\,\mbox{Pa}\,,\]

  což je obrovský tlak – pro srovnání řádově 10²⁸-krát větší, než je tzv. normální atmosférický tlak (1013,25 hPa), na který jsme zvyklí.

• Odpověď

  a) Tlak na vnitřní stěnu sféry o poloměru R, vyvolaný přítomností částice o hmotnosti m v základním stavu uvnitř této sféry, je roven

  \[p=\frac{\pi \hbar^2}{4m R^5}\,.\]

  b) V případě elektronu uvnitř sféry o poloměru R = 10⁻¹⁰ m by šlo o tlak 10¹² Pa.

  c) V případě protonu v jádře atomu o poloměru R = 10⁻¹⁵ m by šlo o tlak přibližně 5,2·10³³ Pa, tedy obrovský tlak – pro srovnání řádově 10²⁸-krát větší, než je tzv. normální atmosférický tlak (1013,25 hPa), na který jsme zvyklí.

• Odkaz

  Srovnej s úlohou Síla na stěnu pravoúhlé jámy této sbírky.