Sbírka řešených úloh

Degenerace energie v trojrozměrné nekonečné potenciálové jámě

Úloha číslo: 2016

Částice je uzavřená v trojrozměrné nekonečně hluboké potenciálové jámě.

Napište podmínky pro rozměry této jámy tak, aby existovala alespoň jedna energetická hladina, jejíž stupeň degenerace je alespoň tři.

Napište velikost energie této hladiny a alespoň tři vlnové funkce odpovídající různým stacionárním stavům, které příslušejí dané energetické hladině.

• Nápověda 1

  Úlohy s trojrozměrnou nekonečně hlubokou potenciálovou jámou řešíme převedením problému separací proměnných na tři jednorozměrné nekonečně hluboké potenciálové jámy.

  Zkuste napsat nebo vyhledejte stacionární stavy a energie pro trojrozměrnou nekonečně hlubokou potenciálovou jámu.

• Řešení nápovědy 1

  Stacionární Schrödingerovu rovnici \[\hat{H}\psi(x,y,z)=E\psi(x,y,z)\] pro trojrozměrnou nekonečně hlubokou potenciálovou jámu s potenciálem \[ V(x,y,z) \begin{cases} =0 & \quad \text{pro } x\in\langle 0,a\rangle,\, y\in\langle 0,b\rangle,\, z\in\langle 0,c\rangle, \\ \to\infty & \quad \text{jinak} \\ \end{cases}\] řešíme separací proměnných \(x, y, z\) tím, že napíšeme vlnovou funkci ve tvaru \[\psi(x,y,z)=\psi_x(x)\psi_y(y)\psi_z(z)\] a celkovou energii jako součet energií \[E=E_x+E_y+E_z.\] Tak převedeme jednu složitou rovnici o třech neznámých \[-\frac{\hbar^2}{2m}\left( \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right) \psi(x,y,z)=E\psi(x,y,z)\] na tři jednodušší rovnice o jedné neznámé \[-\frac{\hbar^2}{2m}\frac{\,\mathrm{d}^2\psi_x(x)}{\,\mathrm{d}x^2}=E_x\psi_x(x),\] \[-\frac{\hbar^2}{2m}\frac{\,\mathrm{d}^2\psi_y(y)}{\,\mathrm{d}y^2}=E_y\psi_y(y),\] \[-\frac{\hbar^2}{2m}\frac{\,\mathrm{d}^2\psi_z(z)}{\,\mathrm{d}z^2}=E_z\psi_z(z).\] Místo řešení jedné trojrozměrné nekonečně hluboké potenciálové jámy máme vyřešit tři jednorozměrné nekonečně hluboké potenciálové jámy, jejichž řešení dokonce již známe, jsou to stacionární stavy \[\psi_k(x)=\sqrt{\frac{2}{a}}\sin{\left(\frac{\pi kx}{a}\right)}\quad \text{pro } x\in\langle 0,a\rangle,\] \[\psi_l(y)=\sqrt{\frac{2}{b}}\sin{\left(\frac{\pi ly}{b}\right)}\quad \text{pro } y\in\langle 0,b\rangle,\] \[\psi_n(z)=\sqrt{\frac{2}{c}}\sin{\left(\frac{\pi nz}{c}\right)}\quad \text{pro } z\in\langle 0,c\rangle\] a energie \[E_k=\frac{\pi^2 \hbar^2}{2ma^2}k^2,\] \[E_l=\frac{\pi^2 \hbar^2}{2mb^2}l^2,\] \[E_n=\frac{\pi^2 \hbar^2}{2mc^2}n^2,\] kde \(k\), \(l\), \(n\) jsou přirozená čísla.

  Trojrozměrná nekonečně hluboká potenciálová jáma má stacionární stavy pro \(x\in\langle 0,a\rangle,\, y\in\langle 0,b\rangle,\, z\in\langle 0,c\rangle\) ve tvaru \[\psi_{kln}(x,y,z)=\psi_k(x)\psi_l(y)\psi_n(z)=\sqrt{\frac{2^3}{abc}}\sin{\left(\frac{\pi kx}{a}\right)}\sin{\left(\frac{\pi ly}{b}\right)}\sin{\left(\frac{\pi nz}{c}\right)},\] a energie \[E_{kln}=E_k+E_l+E_n=\frac{\pi^2 \hbar^2}{2m}\left(\frac{k^2}{a^2}+\frac{l^2}{b^2}+\frac{n^2}{c^2}\right),\]

  kde \(k\), \(l\), \(n\) jsou přirozená čísla a \(a\), \(b\), \(c\) jsou rozměry jámy.

• Nápověda 2

  Připomeňte si význam termínů degenerovaná energetická hladina a stupeň degenerace.

• Řešení nápovědy 2

  Energetická hladina je degenerovaná, pokud dané energii, vlastnímu číslu hamiltoniánu, přísluší více různých stavů, tedy stavů, které jsou popsány navzájem lineárně nezávislými funkcemi.

  Stupeň degenerace energetické hladiny udává počet různých stavů s danou energií.

• Nápověda 3

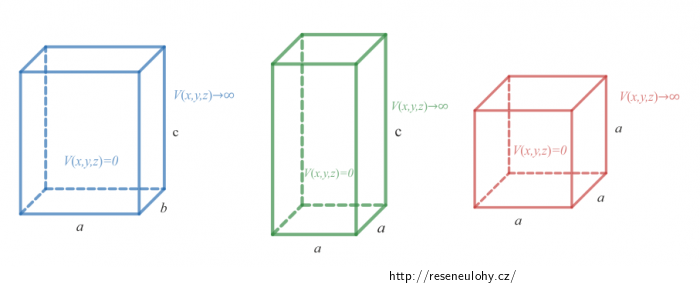
  Degenerované energetické hladiny se často vyskytují v úlohách s velkou symetrií. Promyslete, jaký tvar musí mít jáma, aby měla velkou symetrii.

• Řešení nápovědy 3

  Trojrozměrná pravoúhlá nekonečně hluboká potenciálová jáma o rozměrech \(a\), \(b\), \(c\) bude symetrická, pokud budou alespoň dva rozměry jámy stejné.

  Tento požadavek splňuje už jáma tvaru kvádru, kde \(a=b\neq c\), ale jáma tvaru krychle, kde \(a=b=c\), bude ještě „symetričtější“. Prozkoumáme tedy jámu tvaru krychle.

  

• Řešení

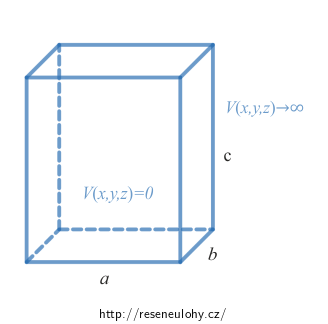
  Trojrozměrná nekonečně hluboká potenciálová jáma s potenciálem \[ V(x,y,z) \begin{cases} =0 & \quad \text{pro } x\in\langle 0,a\rangle,\, y\in\langle 0,b\rangle,\, z\in\langle 0,c\rangle, \\ \to\infty & \quad \text{jinak} \\ \end{cases}\] má pro \(x\in\langle 0,a\rangle,\, y\in\langle 0,b\rangle,\, z\in\langle 0,c\rangle\) stacionární stavy a energie ve tvaru \[\psi_{kln}(x,y,z)=\psi_k(x)\psi_l(y)\psi_n(z)=\sqrt{\frac{2^3}{abc}}\sin{\left(\frac{\pi kx}{a}\right)}\sin{\left(\frac{\pi ly}{b}\right)}\sin{\left(\frac{\pi nz}{c}\right)},\] \[E_{kln}=E_k+E_l+E_n=\frac{\pi^2 \hbar^2}{2m}\left(\frac{k^2}{a^2}+\frac{l^2}{b^2}+\frac{n^2}{c^2}\right),\] kde \(k\), \(l\), \(n\) jsou přirozená čísla a \(a\), \(b\), \(c\) jsou rozměry jámy.

   

  V degenerovaných energetických hladinách existuje více stavů popsaných lineárně nezávislými funkcemi se stejnou energií. Počet těchto stavů se nazývá stupeň degenerace.

  Ze vztahu pro výpočet energie \[E_{kln}=\frac{\pi^2 \hbar^2}{2m}\left(\frac{k^2}{a^2}+\frac{l^2}{b^2}+\frac{n^2}{c^2}\right)\] je vidět, že pro danou částici závisí hodnota energie na rozměrech jámy \(a\), \(b\), \(c\) a na stavech určených čísly \(k\), \(l\), \(n\). Pro různé trojice kvantových čísel \(k\), \(l\), \(n\) jsou stacionární stavy \(\psi_{kln}\) navzájem lineárně nezávislé.

  Obecně platí, že degenerace se vyskytuje v symetrických situacích. Čím bude symetrie jámy větší, tím očekáváme vyšší degeneraci. Maximální symetrii má jáma ve tvaru krychle (viz Řešení nápovědy 3), zvolme tedy \[a=b=c=L\]

  a vyjádřeme stacionární stavy a hodnoty energie pro nekonečně hlubokou potenciálovou jámu tvaru krychle pro \(x\in\langle 0,L\rangle,\, y\in\langle 0,L\rangle,\, z\in\langle 0,L\rangle\)

  \[\psi_{kln}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{\pi kx}{L}\right)}\sin{\left(\frac{\pi ly}{L}\right)}\sin{\left(\frac{\pi nz}{L}\right)},\] \[E_{kln}=\frac{\pi^2 \hbar^2}{2mL^2}\left(k^2+l^2+n^2\right).\]

  Hladina, jejíž stupeň degenerace je alespoň tři, je určena trojicí kvantových čísel, z nichž jsou nejvýše dvě čísla stejná. Například pro trojici přirozených čísel 1, 1 a 2 je velikost energie degenerované hladiny

  \[E_{112}=E_{121}=E_{211}=\frac{\pi^2 \hbar^2}{2mL^2}\left(1+1+4\right)=\frac{3\pi^2 \hbar^2}{mL^2}\]

  a různé stacionární stavy příslušející zvolené energetické hladině popisují vlnové funkce \[\psi_{112}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{\pi x}{L}\right)}\sin{\left(\frac{\pi y}{L}\right)}\sin{\left(\frac{2\pi z}{L}\right)},\] \[\psi_{121}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{\pi x}{L}\right)}\sin{\left(\frac{2\pi y}{L}\right)}\sin{\left(\frac{\pi z}{L}\right)},\] \[\psi_{211}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{2\pi x}{L}\right)}\sin{\left(\frac{\pi y}{L}\right)}\sin{\left(\frac{\pi z}{L}\right)}\] pro \(x\in\langle 0,L\rangle,\, y\in\langle 0,L\rangle,\, z\in\langle 0,L\rangle.\)

   

  Poznámka: Degenerovanou energetickou hladinu lze při vhodných poměrech najít i v jámě tvaru kvádru o třech různých rozměrech \((a\neq b\neq c\neq a)\). Například pro rozměry jámy \(a=L,\, b=2L,\, c=3L\) je minimálně dvakrát degenerovaná energetická hladina

  \[E_{143}=E_{223}=\frac{\pi^2 \hbar^2}{2m}\left(\frac{1^2}{L^2}+\frac{4^2}{(2L)^2}+\frac{3^2}{(3L)^2}\right)=\frac{\pi^2 \hbar^2}{2m}\left(\frac{2^2}{L^2}+\frac{2^2}{(2L)^2}+\frac{3^2}{(3L)^2}\right)=\frac{6\pi^2 \hbar^2}{2mL^2}.\]

• Komentář

  Energetické hladiny nemusí mít stupeň degenerace pouze tři. Uveďme pro ilustraci příklady energetických hladin v krychlové jámě o délce hrany \(L\) s vyššími stupni degenerace.

  Příklad hladiny, jejíž stupeň degenerace je alespoň tři

  \[E_{112}=E_{121}=E_{211}=\frac{6\pi^2 \hbar^2}{2mL^2}.\]

  Příklad hladiny, jejíž stupeň degenerace je alespoň čtyři

  \[E_{115}=E_{151}=E_{511}=E_{333}=\frac{27\pi^2 \hbar^2}{2mL^2}.\]

  Příklad hladiny, jejíž stupeň degenerace je alespoň šest

  \[E_{123}=E_{132}=E_{213}=E_{231}=E_{312}=E_{321}=\frac{14\pi^2 \hbar^2}{2mL^2}.\]

  Příklad hladiny, jejíž stupeň degenerace je alespoň devět

  \[E_{116}=E_{161}=E_{611}=E_{235}=E_{253}=E_{325}=E_{352}=E_{523}=E_{532}=\frac{38\pi^2 \hbar^2}{2mL^2}.\]

  Příklad hladiny, jejíž stupeň degenerace je alespoň dvanáct

  \[E_{127}=E_{172}=E_{217}=E_{271}=E_{712}=E_{721}=E_{255}=E_{525}=E_{552}=E_{336}=E_{363}=E_{633}=\frac{54\pi^2 \hbar^2}{2mL^2}.\]

  Příklad hladiny, jejíž stupeň degenerace je alespoň sedm

  \[E_{157}=E_{175}=E_{517}=E_{571}=E_{715}=E_{751}=E_{555}=\frac{75\pi^2 \hbar^2}{2mL^2}.\]

• Odpověď

  Úlohu splňuje jáma ve tvaru krychle o délce hrany \(L\).

  V krychlové jámě je alespoň třikrát degenerovaná každá hladina, která není popsaná třemi stejnými kvantovými čísly. Velikost energie této hladiny je \[E_{kln}=\frac{\pi^2 \hbar^2}{2mL^2}\left(k^2+l^2+n^2\right)\] a stacionární stavy dané hladiny popisují vlnové funkce \[\psi_{kln}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{\pi kx}{L}\right)}\sin{\left(\frac{\pi ly}{L}\right)}\sin{\left(\frac{\pi nz}{L}\right)},\] kde \(k\), \(l\), \(n\) jsou přirozená čísla, z nichž alespoň jedno má jinou hodnotu, a \(x\in\langle 0,L\rangle,\, y\in\langle 0,L\rangle,\, z\in\langle 0,L\rangle\).

  Například pro trojici přirozených čísel 1, 1 a 2 je velikost energie degenerované hladiny

  \[E_{112}=E_{121}=E_{211}=\frac{3\pi^2 \hbar^2}{mL^2}\]

  a různé stacionární stavy příslušející zvolené energetické hladině popisují vlnové funkce \[\psi_{112}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{\pi x}{L}\right)}\sin{\left(\frac{\pi y}{L}\right)}\sin{\left(\frac{2\pi z}{L}\right)},\] \[\psi_{121}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{\pi x}{L}\right)}\sin{\left(\frac{2\pi y}{L}\right)}\sin{\left(\frac{\pi z}{L}\right)},\] \[\psi_{211}(x,y,z)=\left(\frac{2}{L}\right)^{\frac{3}{2}}\sin{\left(\frac{2\pi x}{L}\right)}\sin{\left(\frac{\pi y}{L}\right)}\sin{\left(\frac{\pi z}{L}\right)}\] pro \(x\in\langle 0,L\rangle,\, y\in\langle 0,L\rangle,\, z\in\langle 0,L\rangle.\)