Jáma ve dvou rozměrech
Úloha číslo: 701
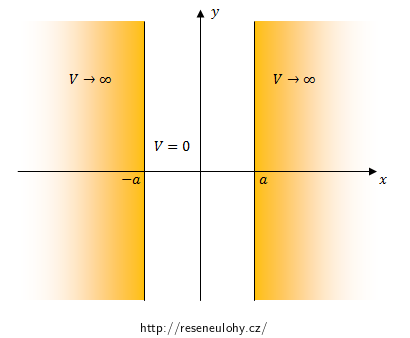
Pohyb částice o hmotnosti m je omezen do dvourozměrné rovinné oblasti, přičemž potenciál V(x, y) = 0 pro −a ≤ x ≤ a, y \(\in\) R a V(x,y) → ∞ všude jinde.
a) Označme Ex energii částice spojenou s pohybem ve směru x, Ey energii spojenou s pohybem ve směru y a celkovou energii částice E. Jakých hodnot mohou energie Ex, Ey a E nabývat?
Dále označme \[k_x = \sqrt{\frac{2mE_x}{\hbar^2}}\] a \[k_y = \sqrt{\frac{2mE_y}{\hbar^2}},\] což je značení obvyklé při řešení odpovídající Schrödingerovy rovnice.
b) Načrtněte graf závislosti E na ky pro několik různých dovolených hodnot Ex.
c) Předpokládejte, že pohyb částice ve směru x odpovídá druhému vázanému stavu v nekonečně hluboké jednorozměrné potenciálové jámě a celková energie částice je rovna E. Najděte energii částice spojenou s jejím pohybem ve směru y.
d) Najděte předpis pro (ne nutně normovanou) vlnovou funkci ψ(x, y, t) popisující stav částice v případě c).
e) Předpokládejte, že celková energie částice je \[E=\frac{\pi^2 \hbar^2}{4ma^2}\,.\] Najděte předpis pro (ne nutně normovanou) vlnovou funkci ψ(x, y, t) popisující stav částice v takovém případě.
f) Předpokládejte, že se nepřekonatelná potenciálová bariéra objeví také v místech se souřadnicí y = ±a. (Pohyb částice bude i ve směru y omezen na úsečku.) Může celková energie částice nabývat hodnoty \[\frac{3\pi^2 \hbar^2}{4ma^2}\,?\] Pokud ano, jak byste takový stav popsali? Pokud ne, proč?
Nápověda k a)
Jaká energie přísluší částici o hmotnosti m ve stavu s kvantovým číslem n v nekonečně hluboké jednorozměrné potenciálové jámě šířky L?
(Podrobné odvození najdete v úloze Symetrická nekonečná pravoúhlá jáma této sbírky.)
Řešení a)
Ve směru x je částice vázána v nekonečně hluboké potenciálové jámě šířky 2a, umístěné mezi x = −a a x = a. Takové situaci odpovídá diskrétní spektrum energií
\[\hspace{30px}E_{x_n}=\frac{n^2 \pi^2 \hbar^2}{2m(2a)^2}=\frac{n^2 \pi^2 \hbar^2}{8ma^2}\,,\] n = 1, 2, ... .
Ve směru y jde o volnou částici s libovolnou kinetickou energií \[E_y \ge 0\,.\]
Celková energie částice E je součtem energií Ex a Ey. Je proto \[E \ge \frac{\pi^2 \hbar^2}{8ma^2}\,.\]
Řešení b)
Úkolem je načrtnout graf závislosti E na ky pro několik dovolených hodnot Ex.
Označili jsme \[k_y = \sqrt{\frac{2mE_y}{\hbar^2}}\,,\] proto je \[E_y = \frac{\hbar^2 k_y^2}{2m}\,,\]
V řešení úkolu a) jsme si připomněli, že \[E_{x_n} = \frac{n^2 \pi^2 \hbar^2}{8ma^2}\,.\]
Z toho již lehce odvodíme závislost
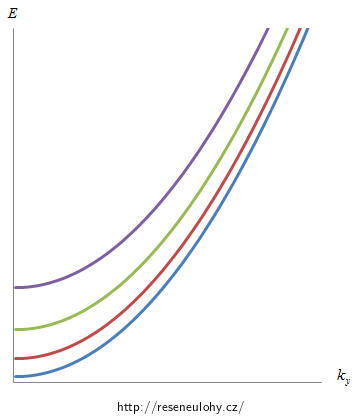
\[E=E_x + E_y = \frac{n^2 \pi^2 \hbar^2}{8ma^2}\,+\,\frac{\hbar^2 k_y^2}{2m}=n^2 E_{x_1}+\frac{\hbar^2}{2m}k_y^2\,.\]Celková energie je úměrná ky2 a pro různá n postupně posunutá o n2-násobky nejnižší energie Ex1, chová se tedy jako E ~ ky2 + n2.
Na následujícím obrázku jsou načrtnuty závislosti E na ky pro n = 1, 2, 3, 4.
Řešení c)
Energie částice odpovídající jejímu pohybu ve směru x má být dle zadání rovna diskrétní hladině s kvantovým číslem n = 2, tedy
\[E_x = E_{x_2} = \frac{4\pi^2\hbar^2}{8ma^2}=\frac{\pi^2 \hbar^2}{2ma^2}\,.\]Energii odpovídající pohybu částice ve směru y dostaneme jako rozdíl její celkové energie a energie Ex. Je
\[E_y=E-E_x=E\,-\,\frac{\pi^2 \hbar^2}{2ma^2}\,.\]Nápověda k d)
Jak vypadají vlastní funkce hamiltoniánu pro případ částice v nekonečně hluboké jednorozměrné potenciálové jámě šířky L se středem v bodě x = 0?
Řešení d)
Jelikož hamiltonián nezávisí na čase, lze separovat obě souřadnice a čas, to znamená vyjádřit celkovou vlnovou funkci jako součin tří funkcí
\[\Psi(x,y,t)=X(x)\,Y(y)\,T(t)\,.\]Ze zadání víme, že co se týče jejího pohybu ve směru x, částice se nachází ve stavu s kvantovým číslem n = 2. Dosazením hodnot L = 2a a n = 2 do obecného předpisu (viz řešení předcházející nápovědy)
\[\psi_n(x)= \sin\left(\frac{n\pi x}{L}\right)\]dostáváme
\[X(x)=\sin\left(\frac{2\pi x}{2a}\right)=\sin\left(\frac{\pi x}{a}\right)\,.\]Ve směru y není pohyb částice omezen. Přísluší jí energie
\[E_y=E\,-\,\frac{\pi^2 \hbar^2}{2ma^2}\,.\]Řešením nečasové Schrödingerovy rovnice
\[\frac{\mbox{d}^2 Y(y)}{\mbox{d}y^2}\,+\,k_y^2\,Y(y)=0\,,\]kde \[k_y=\sqrt{\frac{2mE_y}{\hbar^2}}\,,\] jsou funkce
\[Y(y)=A\,\sin(k_y y)\,+\,B\,\cos(k_y y)\,,\]kde A, B jsou libovolná komplexní čísla.
Z řešení časové části Schrödingerovy rovnice je znám faktor
\[T(t)=e^{-\frac{iEt}{\hbar}}\,,\]který vyjadřuje časovou závislost vlnové funkce popisující stav částice s energií E.
Vrátíme-li se nyní k celkové vlnové funkci \(\Psi(x,y,t)\,,\) dostáváme
\[\Psi(x,y,t)=\sin\left(\frac{\pi x}{a}\right)\,\left[A\,\sin(k_y y)\,+\,B\,\cos(k_y y)\right]\,e^{-\frac{iE t}{\hbar}}\,,\]kde \[k_y=\sqrt{\frac{2mE_y}{\hbar^2}}=\sqrt{\frac{2m}{\hbar^2} \,\left(E\,-\,\frac{\pi^2 \hbar^2}{2ma^2}\right)}=\sqrt{\frac{2mE}{\hbar^2}\,-\,\frac{\pi^2}{a^2}}\,.\]
Řešení e)
Dle předpokladu je celková energie částice rovna
\[E=\frac{\pi^2 \hbar^2}{4ma^2}\,,\]což je více než
\[E_{x_1}=\frac{\pi^2 \hbar^2}{8ma^2}\,,\]ale méně než
\[E_{x_2}=\frac{\pi^2 \hbar^2}{2ma^2}\,.\]Jelikož energie Ex, spojená s pohybem částice ve směru x, může nabývat pouze vybraných diskrétních hodnot, můžeme usoudit, že
\[E_x=E_{x_1}=\frac{\pi^2 \hbar^2}{8ma^2}\,.\]Z pohledu jednorozměrné potenciálové jámy orientované ve směru x se tedy částice nachází ve stavu s kvantovým číslem n = 1.
Na energii Ey, spojenou s pohybem částice ve směru y, nyní zbývá
\[E_y=E-E_x=\frac{\pi^2 \hbar^2}{4ma^2}\,-\,\frac{\pi^2 \hbar^2}{8ma^2}=\frac{\pi^2 \hbar^2}{8ma^2}\,.\]Dále budeme postupovat analogicky jako při řešení úkolu d).
Jelikož hamiltonián nezávisí na čase, lze separovat obě souřadnice a čas, to znamená vyjádřit celkovou vlnovou funkci jako součin tří funkcí
\[\Psi(x,y,t)=X(x)\,Y(y)\,T(t)\,.\]Ze zadání víme, že co se týče jejího pohybu ve směru x, částice se nachází ve stavu s kvantovým číslem n = 1. Dosazením hodnot L = 2a a n = 1 do obecného předpisu (viz Řešení nápovědy k d))
\[\psi_n(x)= \cos\left(\frac{n\pi x}{L}\right)\]dostáváme
\[X(x)=\cos\left(\frac{\pi x}{2a}\right)\,.\]Řešení f)
Dle předpokladu se nyní nepřekonatelná potenciálová bariéra objeví také v místech se souřadnicí y = ±a a pohyb částice je tak i ve směru y omezen na úsečku. Energie Ey, spojená s pohybem částice ve směru y, tak bude stejně jako energie Ex, spojená s pohybem částice ve směru x, kvantována. Možnými hodnotami jsou
\[\hspace{30px}E_{x_{n_x}}=\frac{n_x^2 \pi^2 \hbar^2}{8ma^2}\,\] a \[\,E_{y_{n_y}}=\frac{n_y^2 \pi^2 \hbar^2}{8ma^2}\,,\] kde nx, nx = 1, 2, ... .
(Podrobné odvození kvantování energie naleznete v úloze Symetrická nekonečná pravoúhlá jáma této sbírky.)
Celková energie \(E\) může nabývat hodnot
\[E_{n_x,n_y}=\frac{\pi^2 \hbar^2}{8ma^2}\,\left(n_x^2\,+\,n_y^2\right)\,.\]Nejnižší možné hladiny jsou
\[\hspace{30px}E_{11}=\frac{\pi^2 \hbar^2}{4ma^2}\,,\]
\[\hspace{30px}E_{12}=E_{21}=\frac{5\pi^2 \hbar^2}{8ma^2}\,,\]
\[\hspace{30px}E_{22}=\frac{\pi^2 \hbar^2}{ma^2}\,,\]
\(\hspace{30px}E_{13}=E_{31}=\frac{5\pi^2 \hbar^2}{4ma^2}\) atd.
Hodnota \(\frac{3\pi^2 \hbar^2}{4ma^2}\,\) je větší než E12, ale menší než E22. Diskrétní spektrum energií
stacionárních stavů je jednoznačně dané, proto se částice nemůže nacházet ve vlastním stavu s energií rovnou uvedené hodnotě. Pokud se ale zaměříme na střední hodnoty energie, pak existuje spousta nestacionárních stavů, pro které je zadaná energie právě touto střední hodnotou.
Odpovědi
a) Možné energie jsou diskrétní \(E_{x_n}=\frac{n^2 \pi^2 \hbar^2}{8ma^2}\), n = 1, 2, ..., libovolná \(E_y \ge 0\) a celková \(E \ge \frac{\pi^2 \hbar^2}{8ma^2}\).
c) Energie \(E_x = \frac{\pi^2 \hbar^2}{2ma^2}\) a energie \(E_y=E\,-\,\frac{\pi^2 \hbar^2}{2ma^2}\).
d) Hledaná (nenormovaná) vlnová funkce má tvar
\[\Psi(x,y,t)=\sin\left(\frac{\pi x}{a}\right)\,\left(A\,\sin(k_y y)\,+\,B\,\cos(k_y y)\right)\,e^{-\frac{iE t}{\hbar}}\,,\]kde \[k_y=\sqrt{\frac{2mE}{\hbar^2}\,-\,\frac{\pi^2}{a^2}}\,\] a A, B jsou nějaká komplexní čísla.
e) Hledaná (nenormovaná) vlnová funkce má tvar
\[\Psi(x,y,t)=\cos\left(\frac{\pi x}{2a}\right)\,\left[A\,\sin\left(\frac{\pi y}{2a}\right)\,+\,B\,\cos\left(\frac{\pi y}{2a}\right)\right]\,e^{-\frac{iE t}{\hbar}}\,,\]kde \(E=\frac{\pi^2 \hbar^2}{4ma^2}\,\) a A, B jsou nějaká komplexní čísla.
f) Celková energie částice nemůže nabývat hodnoty \(\frac{3\pi^2 \hbar^2}{4ma^2}\), neboť ta neodpovídá žádné z možných hladin diskrétního energetického spektra.


