Sbírka řešených úloh

Kvark v krabici

Úloha číslo: 684

Kvarky sice nelze pozorovat jako volné částice, nicméně představme si jako modelovou situaci kvark vázaný v nekonečně hluboké třírozměrné potenciálové jámě tvaru krychle o straně délky L = 2,0·10⁻¹⁵ m, což je řádově rozměr protonu či neutronu.

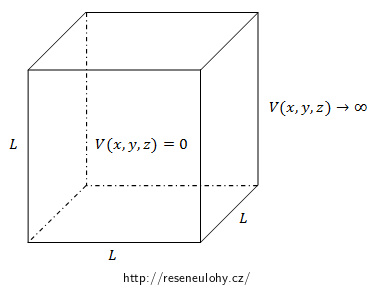
Uvažujme hmotnost kvarku* m_q = 5 MeV/c². Určete v GeV energii potřebnou k přechodu ze základního do prvního excitovaného stavu.

* Jde o přibližnou klidovou hmotnost kvarku down, který je jedním ze stavebních prvků protonů a neutronů. Zdroj: http://pdg.lbl.gov/2010/tables/rpp2010-sum-quarks.pdf.

• Nápověda

  Závislost energie na hmotnosti částice, šířce jámy a dalších parametrech je u třírozměrného problému obdobná jako u analogické situace v jednom rozměru. Kvantování energie je složitější pouze tím, že si vyžaduje použití tří kvantových čísel n_x, n_y a n_z místo jednoho čísla n. Jak tedy přesně vypadá předpis pro E_{nx ny nz}?

• Řešení nápovědy

  Stavu částice o hmotnosti m v nekonečně hluboké potenciálové jámě tvaru krychle o hraně délky L, popsanému trojicí kvantových čísel n_x, n_y a n_z, přísluší energie

  \[E_{n_x^{\,} n_y n_z}=\frac{\pi^2 \hbar^2}{2mL^2}\,\left(n_x^2 + n_y^2 + n_z^2 \right) ,\] kde n_x, n_y, n_z = 1, 2, 3, ... .

• Řešení

  Energie základního stavu kvarku v nekonečně hluboké krychlové potenciálové jámě je

  \[E_{111}=\frac{3\pi^2 \hbar^2}{2m_q L^2}.\]

  Energie prvního excitovaného stavu je

  \[E_{211}=E_{121}=E_{112}=\frac{6\pi^2 \hbar^2}{2m_q L^2} .\]

  Hladina je třikrát degenerovaná.

  Potřebnou excitační energii vypočteme jako rozdíl těchto dvou hladin:

  \[\Delta E = E_{211}-E_{111}=\frac{6\pi^2 \hbar^2}{2m_q L^2}-\frac{3\pi^2 \hbar^2}{2m_q L^2}=\frac{3\pi^2 \hbar^2}{2m_q L^2}=\frac{3h^2}{8m_q L^2} .\]

  Dosazovat budeme hodnotu Planckovy konstanty ve vhodných jednotkách, tj.

  \[h=4{,}136{\cdot}10^{-15}\ \mbox{eV}\cdot \mbox{s}=4{,}136{\cdot}10^{-21}\ \mbox{MeV} \cdot \mbox{s} .\]

  Dostáváme

  \[\Delta E =\frac{3\,\cdot\,\left(4{,}136\,\cdot\,10^{-21}\ \mbox{MeV}\cdot \mbox{s}\right)^2\,\cdot\,\left(3\,\cdot\,10^8\ \mbox{m s}^{-1}\right)^2}{8\,\cdot\,5\ \mbox{MeV}\,\cdot\,\left(2\,\cdot\,10^{-15}\ \mbox{m}\right)^2}=\frac{27\,\cdot\,4{,}136^2}{160}\,\cdot 10^{4}\ \mbox{MeV}\,\dot{=} \,29\ \mbox{GeV}.\]

• Odpověď

  Energie potřebná k přechodu ze základního do prvního excitovaného stavu je rovna přibližně 29 GeV.

• Komentář

  Je nutno podotknout, že uvedený model je sice pěkný, nicméně nepříliš realistický, neboť excitační energie nukleonů jsou řádově rovny stovkám MeV a zde nám vychází v desítkách GeV.