Porucha periodická v čase
Úloha číslo: 2293
Uvažujme systém nacházející se v čase \(t=0\) ve vlastním stavu \(|i\rangle\) neporušeného hamiltoniánu \(\hat{H}_0\). Vypočítejte pravděpodobnost přechodu systému v časovém intervalu \((0,\tau)\) z počátečního stavu do stavu \(|j\rangle\) vlivem poruchy s periodickým časovým průběhem ve tvaru
\[\hat{V}=\hat{\vartheta} e^{i\omega t}+\hat{\vartheta}^\dagger e^{−i\omega t},\]kde \(\hat{\vartheta}\) a \(\hat{\vartheta}^\dagger\) jsou obecné, navzájem hermitovsky sdružené operátory, vyjádřené pomocí \(\hat{x}\) a \(\hat{p}\).
Nápověda 1 – Princip nestacionární poruchové metody
Připomeňte si princip nestacionární poruchové metody v kvantové mechanice. Nemáte-li přístup k vlastním poznámkám, můžete nahlédnout v sekci Časově konstantní porucha, Řešení nápovědy 1 na její stručné zopakování.
Řešení
Zajímá nás pravděpodobnost přechodu systému vlivem zadané poruchy do vlastního stavu \(|j\rangle\). Spočítejme proto koeficient \(c_j^{(p)}(t)\), který stojí před vlastním stavem \(|j\rangle\) v lineární kombinaci pro konečný stav systému při vypnutí poruchy. Dosaďme do vzorce, který platí v prvním řádu poruchové teorie
\[c_j^{(p)}(\tau)=\frac{1}{i\hbar}\int_{0}^{\tau}\left\langle j\Big|\hat{V}(t)i\right\rangle e^{i\frac{E_j−E_i}{\hbar}t}\, \mathrm{d}t.\]Označme
\[\left\langle j\Big|\hat{\vartheta}i\right\rangle=\vartheta_{ji},\] \[\left\langle j\bigg|\hat{\vartheta}^\dagger i\right\rangle=\vartheta_{ji}^\dagger,\] \[\frac{E_j−E_i}{\hbar}=\omega_{ji}.\]Díky hermitovosti operátorů platí
\[\vartheta_{ji}^\dagger=\left\langle j\bigg|\hat{\vartheta}^\dagger i\right\rangle=\left\langle\hat{\vartheta} j\Big|i\right\rangle=\left\langle i\Big|\hat{\vartheta} j\right\rangle^\ast=\vartheta_{ij}^\ast.\]Dosaďme nyní do vzorce pro výpočet koeficientu \(c_j^{(p)}(\tau)\) tvar uvažované poruchy
\[c_j^{(p)}(\tau)=\frac{1}{i\hbar}\int_{0}^{\tau}\left\langle j\bigg|\left(\hat{\vartheta} e^{i\omega t}+\hat{\vartheta}^\dagger e^{−i\omega t}\right) i\right\rangle e^{i\omega_{ji}t}\, \mathrm{d}t\]A spočtěme integrál
\[c_j^{(p)}(\tau)=\frac{1}{i\hbar}\int_{0}^{\tau}\left\langle j\Big|\hat{\vartheta} i\right\rangle e^{i\omega t}e^{i\omega_{ji}t}\, \mathrm{d}t+\frac{1}{i\hbar}\int_{0}^{\tau}\left\langle\ j\bigg|\hat{\vartheta}^\dagger i\right\rangle e^{−i\omega t}e^{i\omega_{ji}t}\, \mathrm{d}t=\] \[=\frac{1}{i\hbar}\int_{0}^{\tau}\vartheta_{ji}e^{i(\omega_{ji}+\omega)t}\, \mathrm{d}t+\frac{1}{i\hbar}\int_{0}^{\tau}\vartheta_{ji}^\dagger e^{i(\omega_{ji}−\omega )t}\, \mathrm{d}t=\frac{1}{i\hbar}\vartheta_{ji}\left[\frac{e^{i(\omega_{ji}+\omega)t}}{i(\omega_{ji}+\omega)}\right]_0^\tau+\frac{1}{i\hbar}\vartheta_{ij}^\ast\left[\frac{e^{i(\omega_{ji}−\omega)t}}{i(\omega_{ji}−\omega)}\right]_0^\tau=\] \[=\frac{−1}{\hbar}\vartheta_{ji}\left(\frac{e^{i(\omega_{ji}+\omega)\tau}−1}{\omega_{ji}+\omega}\right)+\frac{−1}{\hbar}\vartheta_{ij}^\ast\left(\frac{e^{i(\omega_{ji}−\omega)\tau}−1}{\omega_{ji}−\omega}\right)=\] \[=\frac{−1}{\hbar}\vartheta_{ji}e^{i\frac{(\omega_{ji}+\omega)}{2}\tau}\left(\frac{e^{i\frac{(\omega_{ji}+\omega)}{2}\tau}−e^{−i\frac{(\omega_{ji}+\omega)}{2}\tau}}{\omega_{ji}+\omega}\right)+\frac{−1}{\hbar}\vartheta_{ij}^\ast e^{i\frac{(\omega_{ji}−\omega)}{2}\tau}\left(\frac{e^{i\frac{(\omega_{ji}−\omega)}{2}\tau}−e^{−i\frac{(\omega_{ji}−\omega)}{2}\tau}}{\omega_{ji}−\omega}\right)=\] \[=\frac{−2i}{\hbar}\vartheta_{ji}e^{i\frac{(\omega_{ji}+\omega)}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{(\omega_{ji}+\omega)}{2}\tau\right)}{\omega_{ji}+\omega}\right)+\frac{−2i}{\hbar}\vartheta_{ij}^\ast e^{i\frac{(\omega_{ji}−\omega)}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{(\omega_{ji}−\omega)}{2}\tau\right)}{\omega_{ji}−\omega}\right)=\] \[=\frac{−i}{\hbar}e^{i\frac{\omega_{ji}}{2}\tau}\left[\vartheta_{ji}e^{i\frac{\omega}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{\omega_{ji}+\omega}{2}\tau\right)}{\frac{\omega_{ji}+\omega}{2}}\right)+\vartheta_{ij}^\ast e^{i\frac{−\omega}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{\omega_{ji}−\omega}{2}\tau\right)}{\frac{\omega_{ji}−\omega}{2}}\right)\right].\]Pravděpodobnost přechodu tedy je
\[P_{i\rightarrow j}=\left|c_j^{(p)}(\tau)\right|^2=\frac{1}{\hbar^2}\left|\vartheta_{ji}e^{i\frac{\omega}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{\omega_{ji}+\omega}{2}\tau\right)}{\frac{\omega_{ji}+\omega}{2}}\right)+\vartheta_{ij}^\ast e^{i\frac{−\omega}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{\omega_{ji}−\omega}{2}\tau\right)}{\frac{\omega_{ji}−\omega}{2}}\right)\right|^2.\]Z grafu funkce \(\frac{\mathrm{sin}(x)}{x}\) vidíme, že funkce nabývá nezanedbatelných hodnot jen na okolí nuly.
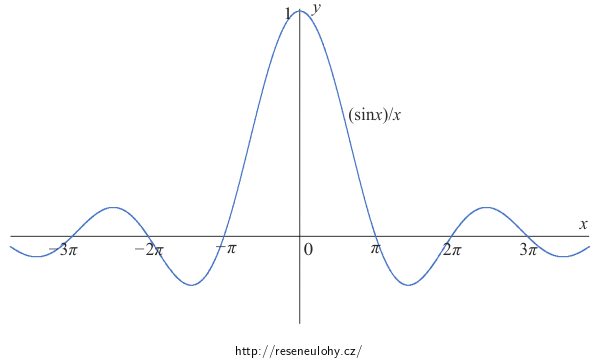
Omezíme-li se na \(\omega_{ji}\) taková, že
\[\frac{\omega_{ji}−\omega}{2}\ll\frac{\omega_{ji}+\omega}{2},\]neboli
\[\omega_{ji}\approx \omega,\]tedy můžeme zanedbat první člen vystupující ve výrazu pro pravděpodobnost přechodu. Pravděpodobnost přechodu pro \(\omega_{ji}\) blízká \(\omega\) je přibližně
\[P_{i\rightarrow j}\doteq\frac{\left|\vartheta_{ij}^\ast\right|^2}{\hbar^2}\left|\frac{\mathrm{sin}\left(\frac{\omega_{ji}−\omega}{2}\tau\right)}{\frac{\omega_{ji}−\omega}{2}}\right|^2.\]Navíc můžeme psát
\[\omega_{ji}−\omega\approx 0 \Rightarrow E_j\approx E_i+\hbar\omega.\]Poslední výraz znamená, že systém přejde do stavu s energií větší o \(\hbar\omega\), což můžeme interpretovat jako absorpci fotonu dopadajícího záření o energii \(\hbar\omega.\)
Podobně můžeme postupovat pro
\[\omega_{ji}\approx −\omega,\]můžeme zanedbat druhý člen vystupující ve výrazu pro pravděpodobnost přechodu. Pravděpodobnost přechodu pro \(\omega_{ji}\) blízká \(−\omega\) je přibližně
\[P_{i\rightarrow j}\doteq\frac{\left|\vartheta_{ji}\right|^2}{\hbar^2}\left|\frac{\mathrm{sin}\left(\frac{\omega_{ji}+\omega}{2}\tau\right)}{\frac{\omega_{ji}+\omega}{2}}\right|^2.\]Analogicky k předchozímu případu je
\[\omega_{ji}+\omega\approx 0 \Rightarrow E_j\approx E_i−\hbar\omega.\]Poslední výraz znamená snížení energie e \(\hbar\omega\) a to můžeme interpretovat jako stimulovanou emisi fotonu o energii \(\hbar\omega.\)
Odpověď
Uvažujeme-li systém nacházející se v čase \(t=0\) ve vlastním stavu \(|i\rangle\) neporušeného hamiltoniánu \(\hat{H}_0\), na který působí porucha \(\hat{V}\) periodická v čase
\[\hat{V}=\hat{\vartheta} e^{i\omega t}+\hat{\vartheta}^\dagger e^{−i\omega t},\]kde \(\hat{\vartheta}\) a \(\hat{\vartheta}^\dagger\) jsou obecné, navzájem hermitovsky sdružené operátory, vyjádřené pomocí \(\hat{x}\) a \(\hat{p}\), pak je pravděpodobnost přechodu systému v časovém intervalu \((0,\tau)\) z počátečního stavu do stavu \(|j\rangle\) rovna
\[P_{i\rightarrow j}=\left|c_j^{(p)}(\tau)\right|^2=\frac{1}{\hbar^2}\left|\vartheta_{ji}e^{i\frac{\omega}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{\omega_{ji}+\omega}{2}\tau\right)}{\frac{\omega_{ji}+\omega}{2}}\right)+\vartheta_{ij}^\ast e^{i\frac{−\omega}{2}\tau}\left(\frac{\mathrm{sin}\left(\frac{\omega_{ji}−\omega}{2}\tau\right)}{\frac{\omega_{ji}−\omega}{2}}\right)\right|^2,\]kde
\[\left\langle j\Big|\hat{\vartheta}i\right\rangle=\vartheta_{ji},\] \[\left\langle j\bigg|\hat{\vartheta}^\dagger i\right\rangle=\vartheta_{ji}^\dagger=\vartheta_{ij}^\ast,\] \[\frac{E_j−E_i}{\hbar}=\omega_{ji}.\]Pro speciální případ \(\omega_{ji}\approx −\omega\) jsou pravděpodobnosti přechodů a energie konečných stavů rovny
\[P_{i\rightarrow j}\doteq\frac{\left|\vartheta_{ji}\right|^2}{\hbar^2}\left|\frac{\mathrm{sin}\left(\frac{\omega_{ji}+\omega}{2}\tau\right)}{\frac{\omega_{ji}+\omega}{2}}\right|^2,\] \[E_j\approx E_i−\hbar\omega\]a pro \(\omega_{ji}\approx \omega\)
\[P_{i\rightarrow j}\doteq\frac{\left|\vartheta_{ij}^\ast\right|^2}{\hbar^2}\left|\frac{\mathrm{sin}\left(\frac{\omega_{ji}−\omega}{2}\tau\right)}{\frac{\omega_{ji}−\omega}{2}}\right|^2,\] \[E_j\approx E_i+\hbar\omega.\]První případ můžeme interpretovat jako stimulovanou emisi fotonu o energii \(\hbar\omega\) a druhý případ jako absorpci fotonu dopadajícího záření o energii \(\hbar\omega\).


