Sbírka řešených úloh

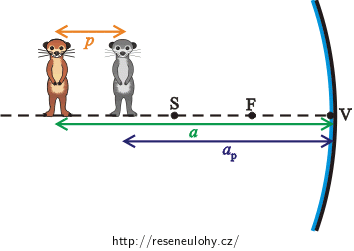
Surikata a ohnisková vzdálenost zrcadla

Úloha číslo: 1919

Obraz surikaty vytvořený dutým zrcadlem je třikrát menší než surikata. Jestliže se surikata přiblíží o půl metru k zrcadlu, je její obraz menší jen dvakrát. Určete ohniskovou vzdálenost zrcadla.

• Nápověda k zápisu

  Pokud je obraz vytvořený dutým zrcadlem menší než předmět, pak je zároveň převrácený. Více se dočtete zde: Zobrazení kulovým zrcadlem.

  Poznámka: Ze znaménkové konvence uvedené v Zobrazení netopýra kulovým zrcadlem a spojnou čočkou plyne, že pro \(Z> 0\) je obraz přímý a pro \(Z< 0\) je obraz převrácený.

• Zápis

  \(Z_{1}= −\frac{1}{3}\)	příčné zvětšení obrazu surikaty (obraz je třikrát menší než surikata)
  \(p=0{,}5 \mathrm{m}\)	vzdálenost, o kterou se surikata posune směrem k zrcadlu
  \(Z_{2}= −\frac{1}{2}\)	příčné zvětšení obrazu surikaty po jejím přiblížení k zrcadlu (obraz je dvakrát menší než surikata)
  \(f= ?\)	ohnisková vzdálenost dutého zrcadla

• Nápověda 1

  Jakým způsobem ovlivňuje ohisková vzdálenost velikost obrazu? Zapište vztah, který tuto skutečnost vyjadřuje, pro příčná zvětšení \(Z_{1}\) a \(Z_{2}\).

• Řešení nápovědy 1

  Pro příčné zvětšení \(Z\) platí vztah: \[Z=−\frac{f}{a−f}.\]

  Přepíšeme pro zvětšení \(Z_{1}\) a \(Z_{2}\): \[Z_{1}=−\frac{f}{a−f},\tag{1}\] \[Z_{2}=−\frac{f}{a_{p}−f},\tag{2}\] kde \(a\) je předmětová vzdálenost před posunutím a \(a_{p}\) je předmětová vzdálenost po posunutí.

• Poznámka

  Pokud si nepamatujete vztah \(Z=−\frac{f}{a−f} (*),\) ale víte, že platí: \[Z=−\frac{a'}{a},\tag{**}\] kde \(a'\) je obrazová vzdálenost, pak můžete využitím zobrazovací rovnice vztah \((*)\) odvodit.

  Napíšeme si zobrazovací rovnici: \[\frac{1}{f}=\frac{1}{a}+\frac{1}{a'}.\] Rovnici budeme upravovat tak, abychom si vyjádřili obrazovou vzdálenost. Od obou stran rovnice odečteme výraz \(\frac{1}{a}\): \[\frac{1}{f}−\frac{1}{a}=\frac{1}{a'}.\] Levou stranu převedeme na společného jmenovatele: \[\frac{a−f}{af}=\frac{1}{a'}.\] Vyjádříme obrazovou vzdálenost: \[a'=\frac{af}{a−f}.\] Získaný vztah dosadíme do rovnice (**): \[Z=−\frac{a'}{a},\] \[Z=−\frac{\frac{af}{a−f}}{a}.\] A po úpravě dostáváme vztah \((*)\): \[Z=−\frac{f}{a−f}.\]

• Nápověda 2

  Surikata se posunula k zrcadlu. Zamyslete se, zda bychom nemohli toto posunutí vyjádřit pomocí nějakých vhodných vzdáleností.

  Následně určete ohniskovou vzdálenost \(f\).

• Řešení nápovědy 2

  Nakreslíme si obrázek.

  

  Z obrázku vidíme, že pro posunutí surikaty bude platit: \[p=a−a_{p}.\tag{3}\]

  Zopakujeme si vztahy (1) a (2):

  \[Z_{1}=−\frac{f}{a−f},\tag{1}\] \[Z_{2}=−\frac{f}{a_{p}−f}.\tag{2}\]

  Z prvního vztahu (1) vyjádříme předmětovou vzdálenost \(a\). Obě strany rovnice vynásobíme \(a−f\) (což můžeme udělat, protože víme, že tento rozdíl je nenulový): \[Z_{1}=−\frac{f}{a−f},\] \[Z_{1}a−Z_{1}f=−f.\] K oběma stranám rovnice přičteme výraz \(Z_{1}f\): \[Z_{1}a=Z_{1}f−f.\] Obě strany rovnice vydělíme \(Z_{1}\): \[a=\frac{Z_{1}f−f}{Z_{1}}.\] \[a=\frac{\left(Z_{1}−1\right)f}{Z_{1}}.\tag{4}\]

  Podobně vyjádříme z druhého vztahu předmětovou vzdálenost \(a_{p}\):

  \[a_{p}=\frac{\left(Z_{2}−1\right)f}{Z_{2}}.\tag{5}\] Dosadíme do rovnice (3) vztahy (4) a (5): \[p=a−a_{p},\] \[p=\frac{\left(Z_{1}−1\right)f}{Z_{1}}−\frac{\left(Z_{2}−1\right)f}{Z_{2}},\] \[p=\left[\frac{\left(Z_{1}−1\right)}{Z_{1}}−\frac{\left(Z_{2}−1\right)}{Z_{2}}\right]f.\] Převedeme zlomky v závorce na společného jmenovatele: \[p=\left[\frac{\left(Z_{1}Z_{2}−Z_{2}\right)−\left(Z_{1}Z_{2}−Z_{1}\right)}{Z_{1}Z_{2}}\right]f.\]

  Upravíme čitatele ve zlomku:

  \[p=\left(\frac{Z_{1}−Z_{2}}{Z_{1}Z_{2}}\right)f.\]

  Výnásobíme obě strany rovnice zlomkem \(\frac{Z_{1}Z_{2}}{Z_{1}−Z_{2}}\): \[\frac{pZ_{1}Z_{2}}{Z_{1}−Z_{2}}=f.\]

  Tím, dostáváme hledanou ohniskovou vzdálenost: \[f=\frac{pZ_{1}Z_{2}}{Z_{1}−Z_{2}}.\]

   

  Číselné řešení

  Dle zadání a zápisu víme: \(Z_{1}= −\frac{1}{3}\), \(Z_{2}= −\frac{1}{2}\), \(p=0{,}5 \mathrm{m}\).

  Dosadíme:

  \(f=\frac{pZ_{1}Z_{2}}{Z_{1}−Z_{2}}=\frac{0{,}5\cdot \left(−\frac{1}{3}\right)\cdot \left(−\frac{1}{2}\right)}{\left(−\frac{1}{3}\right)−\left(−\frac{1}{2}\right)} \mathrm{m}= \frac{0{,}5\cdot \frac{1}{6}}{−\frac{1}{3}+\frac{1}{2}} \mathrm{m}= \frac{0{,}5\cdot \frac{1}{6}}{\frac{−2+3}{6}} \mathrm{m}= \frac{0{,}5\cdot \frac{1}{6}}{\frac{1}{6}} \mathrm{m}= 0{,}5 \mathrm{m}=50 \mathrm{cm}.\)

• Jak víme, že rozdíl předmětové a ohniskové vzdálenosti bude nenulový?

  V předchozím řešení nápovědy jsme psali, že víme, že výraz \(a−f\) je nenulový. Kdyby tento výraz byl nulový, pak by to znamenalo, že předmětová vzdálenost se rovná ohniskové vzdálenosti. V tom případě by se předmět nacházel v ohnisku a výška jeho obrazu by se blížila nekonečnu, což ale v našem případě určitě neplatí.

• Celkové řešení

  Ohnisková vzdálenost a velikost obrazu

  Pomocí příčného zvětšení \(Z\) zapíšeme, jakým způsobem ovlivňuje ohnisková vzdálenost velikost obrazu: \[Z=−\frac{f}{a−f}.\]

  Přepíšeme tento vztah pro zvětšení \(Z_{1}\) a \(Z_{2}\): \[Z_{1}=−\frac{f}{a−f},\tag{1}\] \[Z_{2}=−\frac{f}{a_{p}−f},\tag{2}\] kde \(a\) je předmětová vzdálenost před posunutím a \(a_{p}\) je předmětová vzdálenost po posunutí.

   

  Posunutí surikaty

  

  Z obrázku vidíme, že pro posunutí surikaty bude platit: \[p=a−a_{p}.\tag{3}\]

   

  Vyjádření ohniskové vzdálenosti

  Z prvního vztahu (1) vyjádříme předmětovou vzdálenost \(a\). Obě strany rovnice vynásobíme \(a−f\) (což můžeme udělat, protože víme, že tento rozdíl je nenulový): \[Z_{1}=−\frac{f}{a−f},\] \[Z_{1}a−Z_{1}f=−f.\] K oběma stranám rovnice přičteme výraz \(Z_{1}f\): \[Z_{1}a=Z_{1}f−f.\] Obě strany rovnice vydělíme \(Z_{1}\): \[a=\frac{Z_{1}f−f}{Z_{1}}.\] \[a=\frac{\left(Z_{1}−1\right)f}{Z_{1}}.\tag{4}\]

  Podobně vyjádříme z druhého vztahu předmětovou vzdálenost \(a_{p}\):

  \[a_{p}=\frac{\left(Z_{2}−1\right)f}{Z_{2}}.\tag{5}\] Dosadíme do rovnice (3) vztahy (4) a (5): \[p=a−a_{p},\] \[p=\frac{\left(Z_{1}−1\right)f}{Z_{1}}−\frac{\left(Z_{2}−1\right)f}{Z_{2}},\] \[p=\left[\frac{\left(Z_{1}−1\right)}{Z_{1}}−\frac{\left(Z_{2}−1\right)}{Z_{2}}\right]f.\] Převedeme zlomky v závorce na společného jmenovatele: \[p=\left[\frac{\left(Z_{1}Z_{2}−Z_{2}\right)−\left(Z_{1}Z_{2}−Z_{1}\right)}{Z_{1}Z_{2}}\right]f.\]

  Upravíme čitatele ve zlomku:

  \[p=\left(\frac{Z_{1}−Z_{2}}{Z_{1}Z_{2}}\right)f.\]

  Výnásobíme obě strany rovnice zlomkem \(\frac{Z_{1}Z_{2}}{Z_{1}−Z_{2}}\): \[\frac{pZ_{1}Z_{2}}{Z_{1}−Z_{2}}=f.\]

  Pro hledanou ohniskovou vzdálenost tedy platí: \[f=\frac{pZ_{1}Z_{2}}{Z_{1}−Z_{2}}.\]

   

  Číselné řešení

  Dle zadání a zápisu víme: \(Z_{1}= −\frac{1}{3}\), \(Z_{2}= −\frac{1}{2}\), \(p=0{,}5 \mathrm{m}\).

  Dosadíme:

  \(f=\frac{pZ_{1}Z_{2}}{Z_{1}−Z_{2}}=\frac{0{,}5\cdot \left(−\frac{1}{3}\right)\cdot \left(−\frac{1}{2}\right)}{\left(−\frac{1}{3}\right)−\left(−\frac{1}{2}\right)} \mathrm{m}= \frac{0{,}5\cdot \frac{1}{6}}{−\frac{1}{3}+\frac{1}{2}} \mathrm{m}= \frac{0{,}5\cdot \frac{1}{6}}{\frac{−2+3}{6}} \mathrm{m}= \frac{0{,}5\cdot \frac{1}{6}}{\frac{1}{6}} \mathrm{m}= 0{,}5 \mathrm{m}=50 \mathrm{cm}.\)

• Odpověď

  Ohnisková vzdálenost dutého zrcadla je \(50 \mathrm{cm}.\)