Vrstva oleje na vodě

Úloha číslo: 1578

Na skvrnu oleje tloušťky 0,2 µm vytvořené na vodě dopadá kolmo sluneční světlo. Určete vlnovou délku světla, která se bude po odrazu nejvíce zesilovat. Tato vlnová délka nám určí, jak barevná se nám bude skvrna zdát při pohledu shora.

Nápověda 1
Když světlo dopadne na olej, částečně se odrazí a částečně projde.

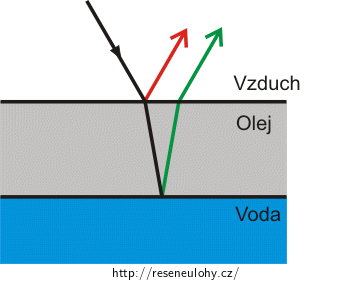
Pro názornost je obrázek namalován pro šikmo dopadající paprsky, ale úlohu řešíme pro kolmo dopadající paprsky.

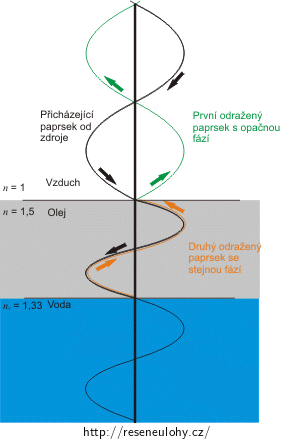
Černý paprsek přichází od zdroje a na prvním rozhraní se část odrazí – tato část je značena jako červený paprsek. Pokračující část paprsku projde olejem a odrazí se na druhém rozhraní – zelený paprsek.

O kolik jsou vzájemně fázově posunuty červený a zelený paprsek?
Nápověda 2
Jak ovlivní fázi vlny její odraz? Jak se tato změna projeví na dráhovém rozdílu?
Řešení nápovědy 2
K odrazu dochází vždy na rozhraní dvou optických prostředí. Jako opticky hustší označujeme to prostředí, které má větší index lomu, a je zde tedy menší rychlost šíření světla.

Rozebereme dva případy, kdy světlo dopadá:

1) z opticky řidšího prostředí na prostředí opticky hustší,

2) z opticky hustšího prostředí na prostředí opticky řidší.

1) Dopad na opticky hustší rozhraní

Černý paprsek dojde od zdroje k rozhraní mezi prostředími. Zde dochází k odrazu na opticky hustším prostředí, a proto zde dojde k odrazu s opačnou fází. Změně fáze na opačnou odpovídá dráhový rozdíl Δl = λ/2.

2) Dopad na opticky řidší rozhraní

Černý paprsek dojde od zdroje k rozhraní mezi prostředími. Zde dochází k odrazu na řidším prostředí, a proto dojde k odrazu se stejnou fází. Tomu odpovídá nulový dráhový rozdíl, tj. Δl = 0.

Tyto děje mají analogii v mechanickém vlnění. Pokud vezmeme provaz, upevníme ho např. ke stěně a zkusíme vyslat vlnu, pevný konec lana způsobí odraz s opačnou fází stejně jako ve výše uvedeném prvním případě. Pokud ovšem necháme lano volně, dojde na jeho konci k odrazu se stejnou fází.
Nápověda 3
Jak se v dráhovém rozdílu projeví skutečnost, že v oleji se světlo šíří pomaleji?
Řešení nápovědy 3
Pokud máme vlnu, která prochází přes prostředí s jinými indexy lomu, dochází zde ke změně vlnové délky.

Geometrická dráha paprsku je stejná jako tloušťka prostředí d. Pro interferenci je ale podstatné, s jakou fází se paprsky potkají, což ovlivňuje nejenom geometrická vzdálenost, kterou urazily, ale i rychlost šíření světla, tj. index lomu prostředí. Chceme zjistit, jakou vzdálenost by světlo urazilo, pokud by místo látkou (zde olejem) letělo vakuem. Protože index lomu n znamená, kolikrát je světlo v daném prostředí pomalejší než ve vakuu, je hledaná vzdálenost, tzv. optická dráha l rovna:
\[l = nd,\]
kde n index lomu prostředí a d je skutečně uražená vzdálenost.
Nápověda 4
Jaký bude celkový dráhový rozdíl obou paprsků?
Řešení nápovědy 4
Nakreslíme si, jak bude vypadat tenká vrstva oleje na vodě a chod obou pro nás podstatných paprsků.

Černý paprsek jde od zdroje a narazí na první rozhraní. Část paprsku se odrazí (v obrázku nakresleno zeleně) a část pokračuje dále ve svém směru. Jedná se o rozhraní vzduch – olej, tedy dochází k odrazu paprsku na opticky hustším prostředí, a proto má zelený paprsek opačnou fázi, což odpovídá dráhovému rozdílu:
\[\mathrm{\Delta}l_\mathrm{1} = \,\frac{\lambda}{2}.\]
Část černého paprsku, která pokračovala ve směru šíření, dorazila na další rozhraní olej – voda, kde dochází k odrazu na opticky řidším prostředí a dráhový rozdíl odraženého oranžového paprsku je dán jen jeho delší dráhou, tedy:
\[\mathrm{\Delta}l_\mathrm{2} =\, \mathrm{2}nd,\]
kde n je index lomu materiálu (v tomto případě oleje), d je tloušťka olejové vrstvy. Tloušťku olejové vrstvy násobíme dvěma, protože paprsek musí projít olejem tam a zpátky, takže geometrickou dráhu musíme započítat dvakrát.

Celkový dráhový rozdíl obou paprsků je dán optickou dráhou, kterou musel oranžový paprsek urazit navíc, a tím, že zelený paprsek změnil při odrazu svoji fázi:
\[\mathrm{\Delta}l = \mathrm{\Delta}l_\mathrm{1} + \mathrm{\Delta}l_\mathrm{2} = \,\frac{\lambda}{2} + \mathrm{2}nd .\]
Toto je vztah pro celkový dráhový rozdíl obou odražených paprsků.
Nápověda 5
Jak poznáme, zda se při interferenci daný paprsek zesílí nebo zeslabí? Tedy, že vzniknou maxima, a nebo minima.
Řešení nápovědy 5
Pro interferenční maxima platí vztah:
\[\mathrm{\Delta}l =\, k\lambda.\]
Pro interferenční minima platí vztah:
\[\mathrm{\Delta}l =\, (2k + 1)\frac{\lambda}{2},\]
kde k je řád maxima/minima, λ je vlnová délka paprsku a Δl je celkový dráhový rozdíl interferujících paprsků.

Podrobnější vysvětlení naleznete – Skládání světla, Řešení nápovědy 1.
Řešení
K odrazu dochází na rozhraní dvou optických prostředí. Pro nás budou důležité první dva odražené paprsky, se kterými budeme dále počítat.

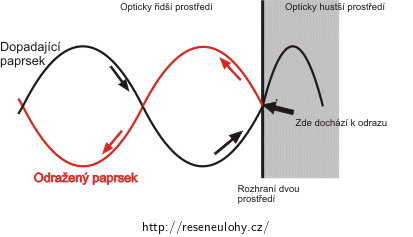
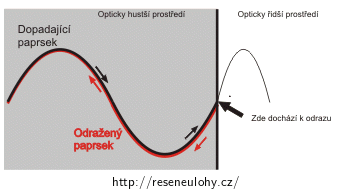
Označujeme jako opticky hustší prostředí, které má větší index lomu, a je zde tedy pomalejší rychlost šíření světla. Rozebereme dva případy, kdy světlo dopadá:

1) z opticky řidšího prostředí na prostředí opticky hustší a odráží se s opačnou fází,

2) z opticky hustšího prostředí na prostředí opticky řidší a odráží se se stejnou fází.

Pro detailnější vysvětlení se podívejte do Nápovědy 2.

Pokud máme vlnu, která prochází přes prostředí s jinými indexy lomu, dochází zde ke změně vlnové délky.

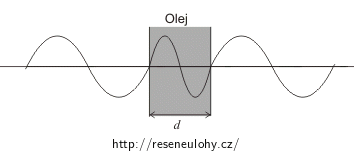
Geometrická dráha paprsku je stejná jako tloušťka prostředí d. Jde nám o to, jakou vzdálenost by světlo urazilo, pokud by místo látkou (zde olejem) letělo vakuem. Protože index lomu n znamená, kolikrát je světlo v daném prostředí pomalejší než ve vakuu, je hledaná vzdálenost, tzv. optická dráha l rovna:
\[l = nd,\]
kde n index lomu prostředí a d je skutečně uražená vzdálenost.

Celkový dráhový rozdíl je dán optickou dráhou, kterou musel první paprsek urazit navíc, a tím, že druhý paprsek změnil při odrazu svoji fázi:
\[\mathrm{\Delta}l = \mathrm{\Delta}l_\mathrm{1} + \mathrm{\Delta}l_\mathrm{2} = \,\frac{\lambda}{2} + 2nd .\tag{1}\]

Při interferenci vznikají maxima a minima.

Pro maxima platí, že rozdíl optických drah se musí rovnat násobku vlnové délky.
\[\mathrm{\Delta}l =\, k\lambda,\tag{2}\]
kde k = (1, 2, 3,...) je řád maxima, λ je vlnová délka paprsku a Δl je celkový dráhový rozdíl.

Podrobnější odvození naleznete – Skládání světla, Řešení nápovědy 1.

Pro výpočet vezmeme rovnice (1) a (2) a dosadíme jednu do druhé. Dostaneme tedy:
\[k\lambda = \,\frac{\lambda}{2} + \mathrm{2}nd\]
a vyjádříme hledanou vlnovou délku λ:
\[\lambda + \mathrm{4}nd = \mathrm{2}k\lambda\] \[\mathrm{4}nd = \lambda(2k − 1)\] \[\lambda = \,\frac{\mathrm{4}nd}{(2k − 1)}\]
Nyní můžeme dosadit za index lomu oleje n = 1,5, tloušťku d = 0,2·10⁻⁶ m a za řád maxima k = 1 .
\[\lambda = \,\frac{4\,\cdot\,1{,}5\,\cdot\,0{,}2 {\cdot}10^{−6}}{(2·1 − 1)}\,\mathrm{m} =\, 1200{\cdot}10^{−9}\,\mathrm{m}.\]
Tato vlnová délka je v infračervené části spektra.

Dosadíme-li za k = 2:
\[\lambda = \,\frac{\mathrm{4}\,\cdot\,1{,}5\,\cdot\,0{,}2 {\cdot}10^{−6}}{(2·2 − 1)}\,\mathrm{m} =\, 400{\cdot}10^{−9}\,\mathrm{m},\]
dostaneme světlo o vlnové délce patřící do viditelného světla.

Dosadíme-li za k = 3:
\[\lambda = \,\frac{\mathrm{4}\,\cdot\,1{,}5\,\cdot\,0{,}2 {\cdot}10^{−6}}{(2·3 − 1)}\,\mathrm{m} =\, 240{\cdot}10^{−9}\,\mathrm{m},\]
vidíme, že toto světlo patří již do ultrafialové části spektra.

Protože očima vnímáme jen viditelnou část spektra, je pro barvu olejové skvrny podstatné řešení pro hodnotu k = 2.
Odpověď
Po odrazu na olejové skvrně se nejvíce zesílí vlnová délka λ = 400 nm (odpovídá pro k = 2), takže ji uvidíme fialovou.