Sbírka řešených úloh

Klínová vrstva

Úloha číslo: 1634

• Obrázek

  

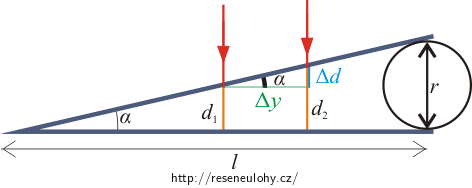
  Na obrázku vyznačíme vše, co známe a co potřebujeme: l je vzdálenost vlasu od společné hrany, r je tloušťka vlasu, α je úhel, který svírají skla, d₁ a d₂ je šířka vrstvy vzduchu mezi skly pro dva sousední světlé proužky a Δy je vzdálenost dvou světlých proužků.

• Nápověda 1

  Jaká je podmínka pro vznik světlých proužků (interferenčních maxim) na vrstvě vzduchu mezi oběma skly? Jaký je rozdíl tloušťky vzduchové vrstvy Δd pro paprsky dvou sousedních maxim?

• Řešení nápovědy 1

  Při dopadu světla na klínovou vrstvu interferují paprsky odražené na rozhraní sklo – vzduch s paprsky odraženými na rozhraní vzduch – sklo. Protože druhý paprsek mění při odrazu svoji fázi, je celkový rozdíl optických drah dán vztahem:

  \[\mathrm{\Delta}l = \,\frac{\lambda}{2} + \mathrm{2}nd. \]

  Podrobné vysvětlení najdete v úloze Vrstva oleje na vodě.

  Světlý proužek vznikne, pokud se rozdíl optických drah rovná násobku vlnové délky (podmínka pro interferenční maximum). Uvažujme dva sousední světlé proužky řádu k a k+1. Napíšeme si dráhové rozdíly těchto světlých proužků:

  \[k\lambda = \,\frac{\lambda}{2} + \mathrm{2}nd_\mathrm{1}. \] \[(k+1)\lambda = \,\frac{\lambda}{2} + \mathrm{2}nd_\mathrm{2}. \]

  Pro rozdíl tloušťky vzduchové vrstvy odečteme druhou rovnici od první a vyjádříme si Δd = d₂ − d₁.

• Nápověda 2

  Vyjádřeme si vztah pro tloušťku vlasu r pomocí úhlu klínové vrstvy α, který svírají sklíčka.

• Řešení nápovědy 2

  

  Z malého trojúhelníku si vyjádříme, jaký vztah platí pro α:

  \[\mathrm{tg}\, \alpha=\, \frac{\mathrm{\Delta}d}{\mathrm{\Delta}y}=\,\frac{d_\mathrm{2} − d_\mathrm{1}}{\mathrm{\Delta}y},\]

  kde Δd je rozdíl tloušťky vzduchové vrstvy pro dvě sousední maxima a Δy je vzdálenost dvou světlých proužků.

  Z velkého trojúhelníku si také vyjádříme vztah pro úhel α:

  \[\mathrm{tg}\,\,\alpha=\, \frac{r}{l},\]

  kde r je tloušťka vlasu a l je vzdálenost vlasu od společné hrany.

  Můžeme dosadit jednu rovnici do druhé za tg α a získáme vztah:

  \[\frac{\mathrm{\Delta}d}{\mathrm{\Delta}y}=\, \frac{r}{l},\]

  kde máme dvě neznámé, tloušťku vlasu r a rozdíl tloušťky vzduchové vrstvy Δd, který jsme si ovšem odvodili v předchozí nápovědě, kde jsme zjistili, že \(\mathrm{\Delta}d=\,\frac{\lambda}{\mathrm{2}n}\).

  Dosadíme za Δd do předchozí rovnice a vyjádříme si r.

• Zápis

  λ = 650 nm = 6,5·10−7 m	vlnová délka světla
  Δy = 1,6 mm  = 1,6·10−3 m	vzdálenost dvou světlých proužků
  l = 25 cm = 0,25 m	vzdálenost vlasu od společné hrany sklíček
  n = 1	index lomu vzduchu
  r = ? (µm)	tloušťka vlasu

• Řešení

  

  Nejprve si nakreslíme obrázek a označíme jednotlivé vzdálenosti: l je vzdálenost vlasu od společné hrany, r je tloušťka vlasu, α je úhel, který svírají skla, d₁ a d₂ je šířka vrstvy mezi skly pro jednotlivé světlé proužky a Δy je vzdálenost dvou světlých proužků.

   

  Při dopadu světla na klínovou vrstvu interferují paprsky odražené na rozhraní sklo – vzduch s paprsky odraženými na rozhraní vzduch – sklo. Celkový dráhový rozdíl je dán vztahem (viz nápověda 1):

  \[\mathrm{\Delta}l = \,\frac{\lambda}{2} + \mathrm{2}nd. \]

   

  Abychom odvodili rozdíl tloušťky vzduchové vrstvy Δd pro paprsky dvou sousedních maxim, vezmeme dva světlé proužky řádu k a k+1 a napíšeme si dráhové rozdíly pro tyto světlé proužky. Víme, že budou splňovat podmínku maxim, totiž Δl = kλ:

  \[k\lambda = \,\frac{\lambda}{2} + \mathrm{2}nd_\mathrm{1}. \] \[(k+1)\lambda = \,\frac{\lambda}{2} + \mathrm{2}nd_\mathrm{2}. \]

  Pro rozdíl tloušťky vzduchové vrstvy odečteme druhou rovnici od první:

  \[(k+1)\lambda − k\lambda =\,\frac{\lambda}{2} + \mathrm{2}nd_\mathrm{2} − \,\frac{\lambda}{2} − \mathrm{2}nd_\mathrm{1}.\]

  a vyjádříme si Δd = d₂ − d₁:

  \[\lambda=\, \mathrm{2}n(d_\mathrm{2} − d_\mathrm{1}),\] \[(d_\mathrm{2} − d_\mathrm{1})=\,\frac{\lambda}{\mathrm{2}n}. \]

   

  Z malého trojúhelníku si vyjádříme, jaký vztah platí pro úhel α:

  \[\mathrm{tg}\, \,\alpha=\, \frac{\mathrm{\Delta}d}{\mathrm{\Delta}y}=\,\frac{d_\mathrm{2} − d_\mathrm{1}}{\mathrm{\Delta}y},\]

  Z velkého trojúhelníku si také vyjádříme vztah pro úhel α:

  \[\mathrm{tg}\, \,\alpha=\, \frac{r}{l},\]

  kde r je tloušťka vlasu a l je vzdálenost vlasu od společné hrany.

  Dosadíme jednu rovnici do druhé za tg α a získáme vztah:

  \[\frac{\mathrm{\Delta}d}{\mathrm{\Delta}y}=\, \frac{r}{l},\]

  máme zde dvě neznámé, tloušťku vlasu r a rozdíl tloušťky vzduchové vrstvy Δd, který jsme si odvodili výše, dosadíme ho sem a vyjádříme si r:

  \[r=\, \frac{l\lambda}{\mathrm{2}n\mathrm{\Delta}y}.\]

  Dosadíme hodnoty ze zadání a dostaneme:

  \[r=\, \frac{0{,}25\,\cdot\,6{,}5{\cdot}10^{−7}}{2\,\cdot\,1\,\cdot\,1{,}6{\cdot}10^{−3}}\dot{=}\,51\,\mathrm{\mu m}.\]

• Odpověď

  Tloušťka vlasu je 51 μm.